こんにちは。ねこの数式のnanakoです。
高校生になって一番初めに習うのが『展開・因数分解』です。これからの数学生活でずっとお世話になるものばかりです。
しっかりと出来るようにして、最高のスタートダッシュを切りましょう。
まずは展開について見ていきます。頑張りましょう♪
展開公式
中学の展開公式の確認!
念のために中学校の展開公式を確認しておきますね。
\(\small(1) (x+a)(x+b)=x^2+(a+b)x+ab\)
\(\small(2) (x+y)^2=x^2+2xy+y^2\)
\(\small(3) (x+y)(x-y)=x^2-y^2\)
例.
\(\small\begin{align}
(1) (x+2)(x+3)&=x^2+(2+3)x+2\times3\\
&=x^2+5x+6
\end{align}\)
\(\small\begin{align}
(2) (x+3y)^2&=x^2+2\cdot x \cdot 3y+(3y)^2\\
&=x^2+6xy+9y^2
\end{align}\)
\(\small\begin{align}
(3) (2x+1)(2x-1)&=(2x)^2-1^2\\
&=4x^2-1
\end{align}\)
では、さっそく高校の内容に入っていきますよ~
高校の展開公式を紹介!
\(\small(1) (a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
\(\small(2) (a+b)^3=a^3+3a^2b+3ab^2+b^3\)
\(\small(3) (a-b)^3=a^3-3a^2b+3ab^2-b^3\)
\(\small(4) (a+b)(a^2-ab+b^2)=a^3+b^3\)
\(\small(5) (a-b)(a^2+ab+b^2)=a^3-b^3\)
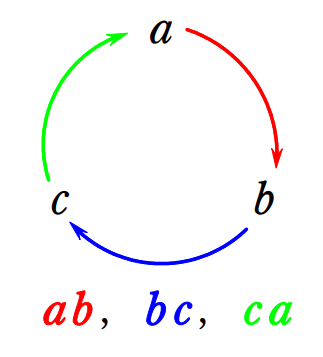
\(\small (1)\) の \(\small ca\) に違和感を感じた人は、いいところに目をつけましたね。
中学校ではアルファベット順と習いましたが、これは高校でよくある例外です。
この公式では、\(\small a\) → \(\small b\) → \(\small c\) → \(\small a\) と1周するイメージで文字並べます。
\(\small (2)\) ~ \(\small (5)\) は数Ⅱの公式ですが、このタイミングで習う高校がほとんどなので、ここで習得しておきましょう。
ただし、\(\small (3)\) は覚えずに \(\small (2)\) を流用した方が良いと思います。ちなみに \(\small (4)\) と \(\small (5)\) は主に因数分解で使います。
では、実際に下の例題で使い方を確認してみましょう。
次の式を展開せよ。
\(\small(1) (x+2y-z)^2\)
\(\small(2) (x-2y)^3\)
\(\small(3) (2x-y)(4x^2+2xy+y^2)\)
\(\small(1)\) \(\small x\,と\,(2y)\,と\,(-z)\) を足していると考えれば公式が使えます。
\(\small\begin{align}
&(x+2y-z)^2\\
=\,&\{x+(2y)+(-z)\}^2\\
=\,&x^2+(2y)^2+(-z)^2+2\cdot x\cdot (2y)+2\cdot (2y)\cdot (-z)+2\cdot (-z)\cdot x\\
=\,&x^2+4y^2+z^2+4xy-4yz-2zx
\end{align}\)
\(\small(2)\) \(\small(1)\) と同じように足し算にしてしまえば、公式の \(\small (2)\) が使えますね。
\(\small\begin{align}
&(x-2y)^3\\
=\,&\{x+(-2y)\}^3\\
=\,&x^3+3\cdot x^2\cdot (-2y)+3\cdot x\cdot (-2y)^2+(-2y)^3\\
=\,&x^3-6x^2y+12xy^2-8y^3
\end{align}\)
\(\small\begin{align}
(3) &(2x-y)(4x^2+2xy+y^2)\\
=\,&\{(2x)-y\}\{(2x)^2+(2x)\cdot y+y^2\}\\
=\,&(2x)^3-y^3\\
=\,&8x^3-y^3
\end{align}\)
お疲れ様でした。公式の使い方は大丈夫そうですかね? 続いては展開の仕方を工夫してみましょう。
展開の仕方の工夫
「どんな問題でも気合と根性で展開できちゃうから、工夫なんてしなくて良いよ~」って思われるかもしれません。
しかしながら、今後の数学生活で色々な場面で使うので、ここで出来るようにしないと損をし続けることになります。
さらにさらに、展開だけではなく因数分解のときにも使う工夫がでてきます。
因数分解のときに困らないように、ここで頑張っておきましょう!
置き換えを利用!
『置き換え』は数学ではよく使う方法です。置き換えることで数式を簡単にして、問題を解きやすくします。さっそく見てみましょう。
次の式を展開せよ。
\(\small(1) (x+1)(x+2)(x+3)(x+4)\)
\(\small(2) (x+1)(x+2)(x+3)(x+6)\)
\(\small (1)\)、\(\small (2)\) どちらも、適切でない組で展開しようとすると、とんでもない計算量となるので、うまい組み合わせで展開します。
\(\small x\) の後ろにある数を和か積で同じ数になるように組を作って、展開しましょう!
\(\small(1)\) \(\small x\) の後ろにある数 \(\small1,\,\,2,\,\,3,\,\,4\) の和が同じになるように 2 組に分けて、展開しましょう。
\(\small\begin{eqnarray}
& &(x\color{red}{+1})(x\color{blue}{+2})(x\color{blue}{+3})(x\color{red}{+4})\\
&=&(x\color{red}{+1})(x\color{red}{+4})(x\color{blue}{+2})(x\color{blue}{+3})\\
&=&(\color{magenta}{x^2+5x}+4)(\color{magenta}{x^2+5x}+6)\\
\end{eqnarray}\)
\(\small\, =(\color{magenta}{A}+4)(\color{magenta}{A}+6) (\color{magenta}{x^2+5x=A})\)
\(\small\begin{eqnarray}
&=&A^2+10A+24\\
&=&(x^2+5x)^2+10(x^2+5x)+24\\
&=&x^4+2\cdot x^2\cdot 5x+(5x)^2+10x^2+50x+24\\
&=&x^4+10x^3+35x^2+50x+24\\
\end{eqnarray}\)
\(\small(2)\) 今度はかけ算で同じになるように分けてみましょう。
\(\small (x\color{red}{+1})(x\color{blue}{+2})(x\color{blue}{+3})(x\color{red}{+6})\)
\(\small\,=(x\color{red}{+1})(x\color{red}{+6})(x\color{blue}{+2})(x\color{blue}{+3})\)
\(\small\,=(\color{magenta}{x^2}+7x\color{magenta}{+6})(\color{magenta}{x^2}+5x\color{magenta}{+6})\)
\(\small\,=(\color{magenta}{A}+7x)(\color{magenta}{A}+5x) (\color{magenta}{x^2+6=A}\)\(\small)\)
\(\small\,=A^2+12xA+35x^2\)
\(\small\,=(x^2+6)^2+12x(x^2+6)+35x^2\)
\(\small\,=x^4+12x^2+36+12x^3+72x+35x^2\)
\(\small\,=x^4+12x^3+47x^2+72x+36\)
先ほど書いた通り、このテクニックは因数分解の際にも使うので、「強引に展開すれば良いじゃん」って思っていると因数分解のときに苦しむので気をつけましょう♪
まとめ and 確認テスト!
高校の展開はいかがでしたでしょうか?これからの数学の問題を解く上で、必要なものばかりです。
また、因数分解をする際にも使う公式や工夫など重要なものが多いです。
高校数学は難しいと思う人が多いですが、1つずつ出来るようにしていけば、きっと数学を解く楽しみが分かってくると思います。
できるだけ分かりやすく説明していきたいと思いますので、これから一緒にがんばりましょう!
確認テストはこちらから!
続きの内容はこちらから!





コメント