こんにちは。ねこの数式のnanakoです。
今回は数Ⅲ極限の中でも数列の極限を中心に扱います。
極限は数Ⅱの微分法でも出てきましたが、数Ⅲではさらに深堀してみていくので楽しみ(?)にしてください。
数列の極限を紹介!
まずは極限とは何か?
数列など、ある種の数学的対象をひとまとまりに並べて考えたものについての極限(きょくげん、英: limit)がしばしば考察される。直感的には、数の列がある値に限りなく近づくとき、その値のことを数列の極限あるいは極限値といい、この数列は収束するという。収束せず正の無限大、負の無限大、振動することを発散するという。
Wikipediaより
む、むずかしい…
具体例を見ながら考えていきましょう!
数列の極限ってナニ?




このように数列の添え字(番号)を増やしていった際に、項がどうなるかが『数列の極限』です。数列の極限の結果は、『収束』『発散』の2つに分かれます。さらに、発散は『正の無限大』、『負の無限大』、『振動』の3つに分かれます。収束と発散に関しては、問題文でも出てくる言葉なので、覚えておきましょう!
では、簡単な問題で極限の特徴をつかんでいきましょう。


さて、極限のイメージはつかめましたか?次は少しずつ実践的な話を見ていきましょう!
不定形ってナニ?
数Ⅱ微分のときに不定形という言葉を習いましたか?まずは不定形とは何なのか確認していきましょう。


次の不定形を見ていきましょう!
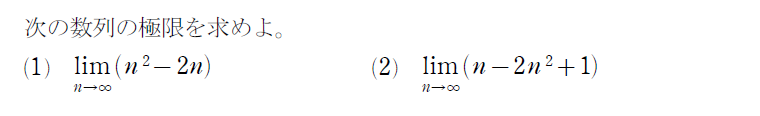

要するに、\(\small n^a \)と\(\small n^b \)で大きい方の影響を受けた結果となるわけです。大きさに関する感覚がポイントになります。
さて、少し実践的な問題を見てみましょう!
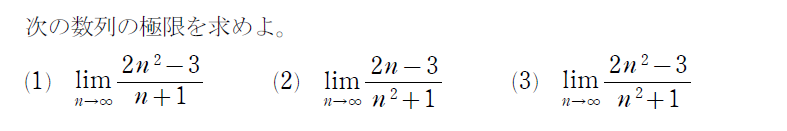

さて、ここまでで不定形が2パターン出てきました。2つのパターンが混ざった問題も存在します。次を見てみましょう!
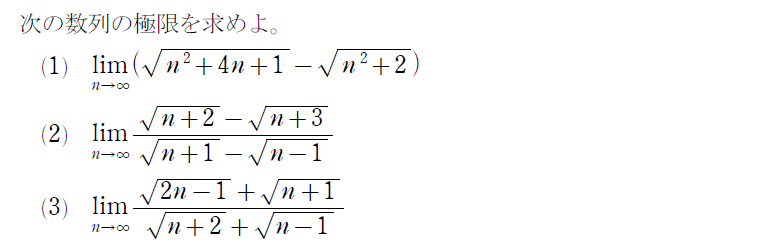

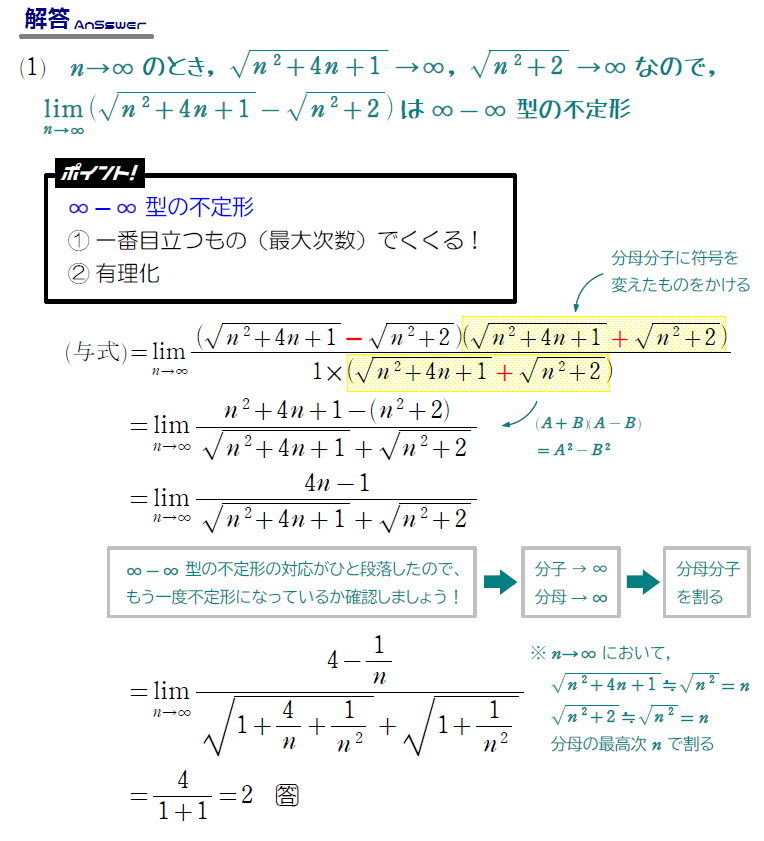

(3)の問題はひっかかりませんでしたか?極限の問題は、「まず近づける」が重要です。式の見た目で計算方法を決めるのではなく、あくまでも不定形の型で計算方法を決めましょう!
無限等比数列ってナニ?
等比数列の添え字\(\small \, n \, \)をどんどん大きくしていったとき、数列の項がどうなるか考えるのが無限等比数列です。

無限等比数列の公式を利用した問題を解いてみましょう!



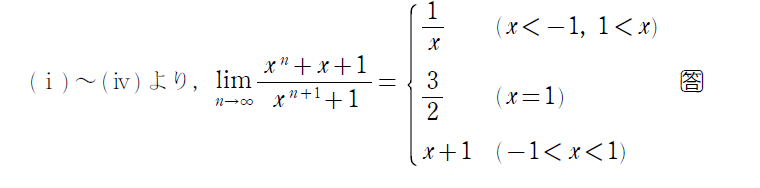
無限等比数列は0に収束する形を利用するのがポイントでした。しっかりと復習しましょう!
無限級数を紹介!
数列の項を無限に足していった結果を無限級数と言います。

本当に無限に足していくことはできないので、第\(\small \, n \, \)項までの和を求め、\(\small \, n \, \)を無限大にすることで、無限級数を疑似的に求めます。
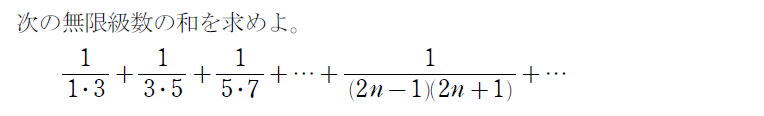

無限等比級数ってナニ?
無限級数の中でも、等比数列の無限級数のことを無限等比級数といいます。さきほど紹介した無限級数の1つなので、同じように解くこともできますが、公式があるので紹介します。


無限等比級数の和の公式は覚えていないと、解けないわけではありませんが、実際の入試問題を解く上では覚えていないと時間的にも計算量的にも厳しいと思うので、必ず覚えて使いこなしていきましょう!
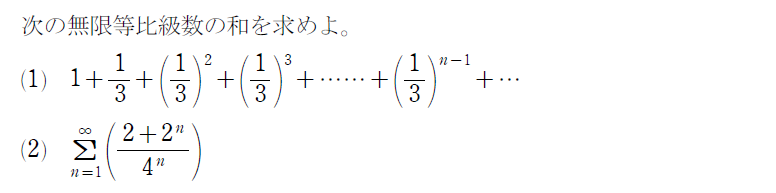

無限等比級数の収束条件ってナニ?
無限等比級数の和を求める方法は大丈夫でしたか?
次は、無限等比級数の収束条件についての問題です。
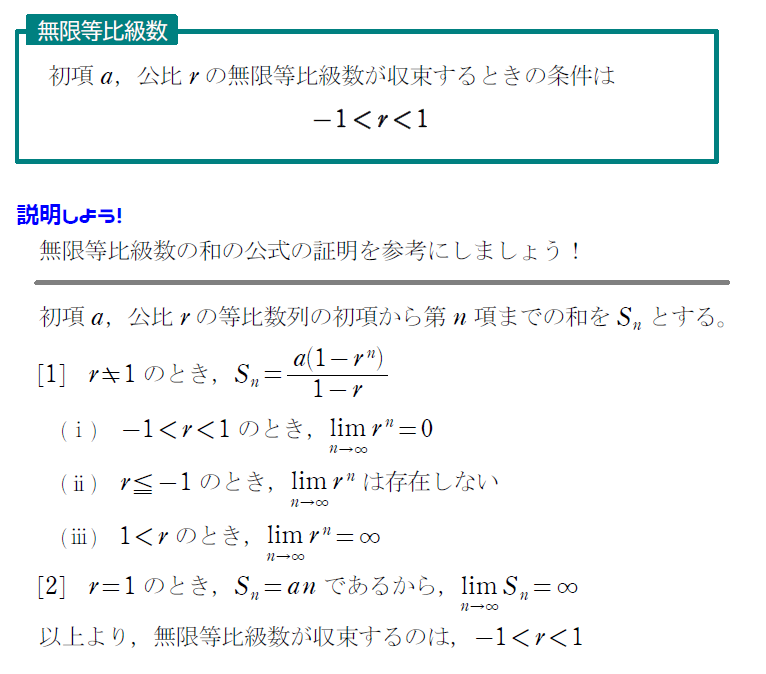


まとめ!
極限の問題は難しいなんて意見も聞きますが、重要なのは、
これを確認するだけで、得意な単元となるので頑張っていきましょう。



コメント