こんにちは。ねこの数式のnanakoです。
今回はシグマの応用問題を紹介していきたいと思います。
公式などの紹介はこちらの記事を参考にしてください。
シグマの応用問題を紹介!
部分分数分解ってナニ?
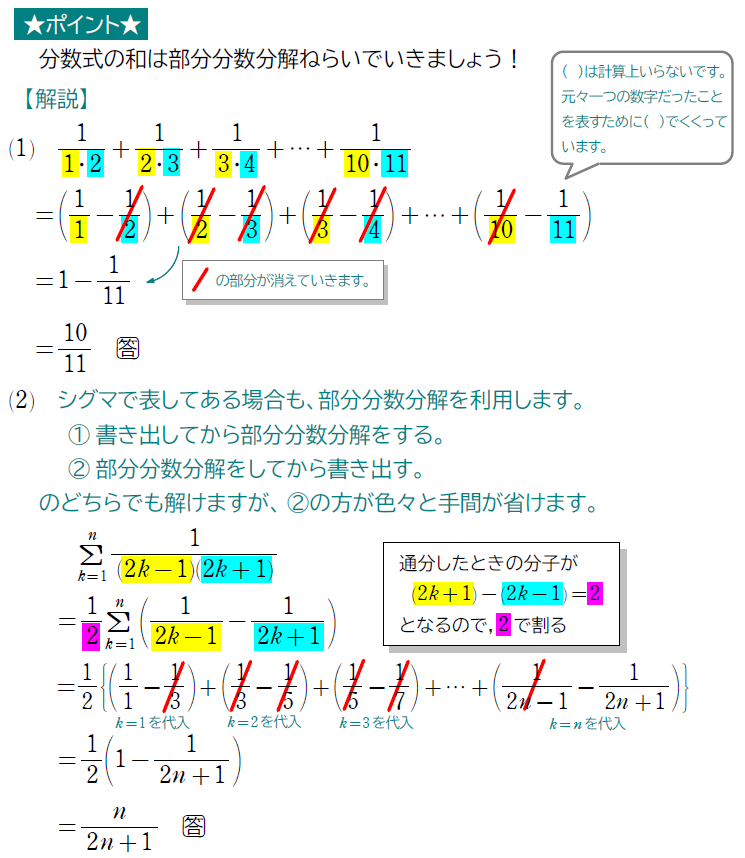
まずは部分分数分解の問題からです。方程式・式と証明という単元で習っている内容であるものの、本格的に利用するのは数列が初めてでしょう。


こんな変形ができたところで、何の役に立つのか…と思っているかもしれませんが、これが超絶役に立つ問題が次の例題です。
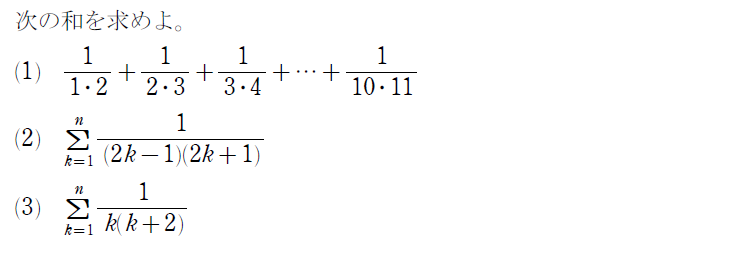


和の和の問題ってナニ?
皆さんは、人間ピラミッドって大好きですよね?(茶番なので次の例題まで流し見でOK…)
人間ピラミッド(にんげんピラミッド)とは組体操の大技のひとつで、人間円塔と並んで演技のクライマックスで披露される。四つんばいになった最下段の演技者の背中の上に同じ姿勢の演技者を積み重ね、上に向かって細くなる三角形状の組み上げを行う。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ということで、いろいろなピラミッドを作ってみたくなってきましたよね?
1段のピラミッド、2段のピラミッド、3段のピラミッド、…、10段のピラミッドまで全部同時に作ってみましょう!
ここで問題となるのが何人必要かということです。
1段のピラミッドは1人
2段のピラミッドは1+2=3人
3段のピラミッドは1+2+3=6人
と10段のピラミッドまで考えていき、その人数の合計だから…
はい!ということで、この話を例題にしたのが以下の問題です!
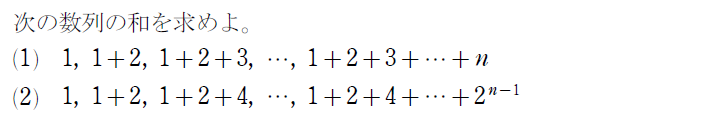

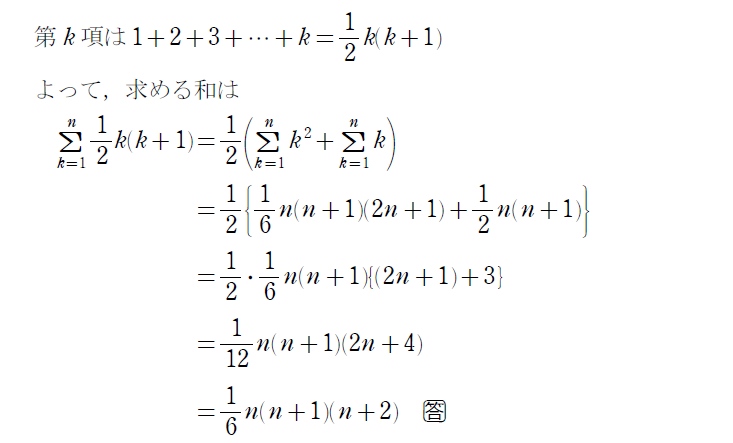

ちなみに先ほどのピラミッドの話は(1)の\(\small \, n \, \)に10を代入した220人が正解です。
等差×等比の問題ってナニ!
突然ですが、次の計算が間違いであることを確認しましょう。
\(\small \color{blue}{1} \cdot \color{red}{3} + \color{blue}{2} \cdot \color{red}{4} = (\color{blue}{1}+\color{blue}{2}) \cdot (\color{red}{3}+\color{red}{4}) \)
左側どうし右側どうし足してから、かけ算をした…ということでしょうが、当然違いますよね。次の間違いも確認しましょう。
\(\displaystyle \sum_{k=1}^{n}(\color{blue}{k} \cdot \color{red}{k})=\sum_{k=1}^{n}\color{blue}{k} \cdot \sum_{k=1}^{n}\color{red}{k} \)
これも間違いですよね。書き出してみると、
(左辺)\(\small = \color{blue}{1} \cdot \color{red}{1} +\color{blue}{2} \cdot \color{red}{2} +\color{blue}{3} \cdot \color{red}{3} + \cdots + \color{blue}{n} \cdot \color{red}{n} \)
(右辺)\(\small = (\color{blue}{1} + \color{blue}{2} +\color{blue}{3} + \cdots +\color{blue}{n})\cdot(\color{red}{1}+\color{red}{2}+\color{red}{3}+ \cdots +\color{red}{n}) \)
1個目の例と同じように間違いですよね。この点に注意しながら次の例題を見ていきましょう!
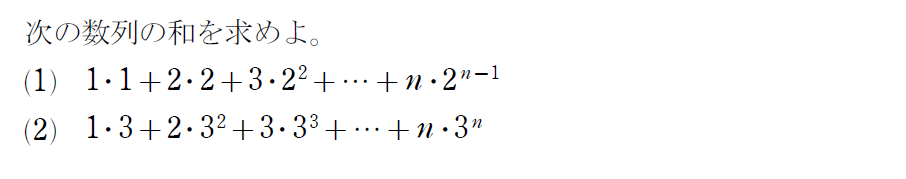




nから始まる数列の和ってナニ?
まずは次の例を見てみましょう!
例.和 \(\small 1 \cdot 3 + 2 \cdot 5 +3 \cdot 7+ \cdots + n(2n+1) \) を求めよ。

シグマを利用して和を求めるために、\(\small k \) 番目を求めましょう!

最後に足しているのが \(\small n \) 番目だから、\(\small n \) を \(\small k \) に変えて、\(\small k(2k+1) \) じゃない?

あとはシグマを利用して、
\(\small \displaystyle \sum_{k=1}^{n}k(2k+1)= \cdots = \frac{1}{6}n(n+1)(4n+5) \)
と求まりましたね。
では、次の問題はどうでしょう?
例.和 \(\small (n+1) + (n+2) +(n+3)+ \cdots + 2n \) を求めよ。

これも同じように考えて、\(\small 2n \) が \(\small n \) 番目だから、\(\small k \) 番目は \(\small 2k \) となるから、
\(\small \displaystyle \sum_{k=1}^{n}2k= \cdots = \frac{1}{3}n(n+1)(2n+1) \)
となるんじゃない?

元の式に \(\small n=1 \) を代入すると \(\small 1+1=2 \) で、
求めた式に \(\small n=1 \)を代入すると \(\displaystyle \small \frac{1}{3}\cdot 1 \cdot 2 \cdot 3=2 \) となるので、
合っていそうにいそうに見えますが、\(\small n=2 \) のときを考えてみましょう。

元の式は \(\small (2+1)+(2+2)=7\) で、求めた式は \(\small \displaystyle \frac{1}{3} \cdot 2 \cdot 3 \cdot 5 =10 \) となって…
あれ?合わない?

そうなんです!ということで、どこが間違いだったのか見ていきましょう!


ということで、正しい解答を見てみましょう!

念のため例題で確認しましょう!(追加の知識も紹介します。)
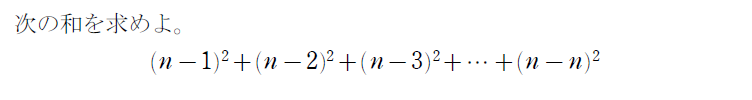


まとめ!
いろいろな数列の和の問題はどうでしたか?理解をしても、いざ自分で解こうとすると手が止まってしまう問題が多いと思うので、他の問題集なども利用して練習をしておきましょう!





コメント