こんにちは。ねこの数式のnanakoです。
シグマという言葉は聞いたことがありますか?
これからの数学でよくお世話になる記号です。この記号により幅広い問題が解けるようになっていくので、さっそく見ていきたいと思います。
シグマを紹介!
シグマってナニ?

突然ですが、1から100までの自然数の和を式にするとどうなりますか?

本当に突然だね。「1+2+3+…+100」でしょ?

「…」を使わないで表してください。

式が長くなりすぎるよ…

ですよねw そんなときに利用するのがシグマです。


自然数の\(\small \, k \, \)番目って、なんて表せますか?

自然数の1番目は1、自然数の2番目は2だから、自然数の\(\small \, k \, \)番目は\(\small \, k \, \)かな?

自然数の1番目から100番目までの和を求めたいので…

\(\small \displaystyle \sum_{k=1}^{100}k \)って表すってこと?

その通りです。例題を通して練習をしてみましょう!
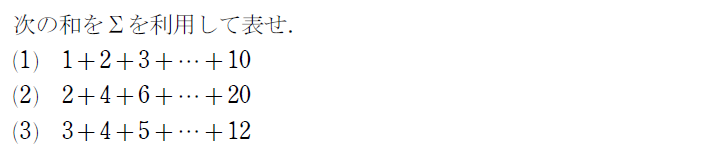


ちなみにΣに利用している \(\small k \) ですが、違う文字を利用して表現しても問題ありません。例えば、さきほどの例題の(2)は、\(\small \displaystyle \sum_{i=1}^{10}2i \) と表す
こともできます。
シグマの公式ってナニ?
さて、シグマを利用した表し方が分かったところで、シグマを利用する理由を紹介します。
シグマを利用するメリットは『式をキレイに見せる』という点と、『計算を楽にする』という点があります。
ということで、続いては『計算を楽にする』ために、シグマの公式を覚えましょう!

定期テストレベルでは証明は関係ないとも言えますが、将来を見越すと②の証明は知っておいて損はないです。


また、次の公式も覚えておきましょう。さきほどの公式よりは直感的に覚えられそうなものです。


シグマを使った問題を紹介!
シグマの公式の使い方ってナニ?
では、公式を利用した問題を見てみましょう!
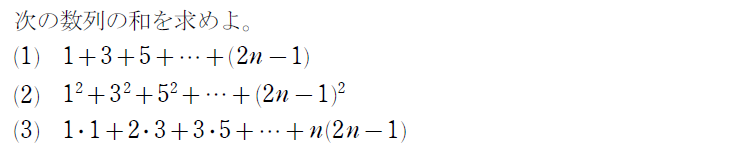
「和を求めよ。」という問題文は、和を\(\small \, n \, \)で表せということです。



実際に見ていきましょう!
シグマと等比のコラボってナニ?
さっそく問題から見てみましょう!


等比数列の和となっていることさえ気づければ、あとは復習ですね。等比数列の和が怪しい人は下の記事も参考にしてください。
まとめ!
シグマの公式は覚えられましたか?ここから扱う数列の問題は、シグマの公式を九九のように扱っていくので、しっかりと使いこなせるようにしていきましょう。





コメント