こんにちは。ねこの数式のnanakoです。
今回は漸化式の紹介です。漸化式の問題の特徴としては、これまで習った数列の知識はもちろん、これから紹介する内容もすぐに次の例題につながってきます。そのため、より一層復習が大切となってくるので頑張っていきましょう!
復習には下の記事を利用してください。
分かりやすい【数列②】シグマを解説!公式の証明も紹介するよ。
分かりやすい【数列③】部分分数分解、等差×等比などいろいろな数列の和を解説!
漸化式を紹介!
漸化式は、各項がそれ以前の項の関数として定まるという意味で数列を再帰的に定める等式である。
ウィキペディア
まぁ、わかりませんよね。ざっくり説明すると、ある等式から元の数列を再現できたら、その等式が漸化式…。もっとざっくり言うと、\(\small a_n \, \)や\(\small \, a_{n+1} \, \)など隣り合った項で作られた等式を漸化式と言います。
とにかく例を見ていきましょう!

同じように項を求める練習をしておきましょう。

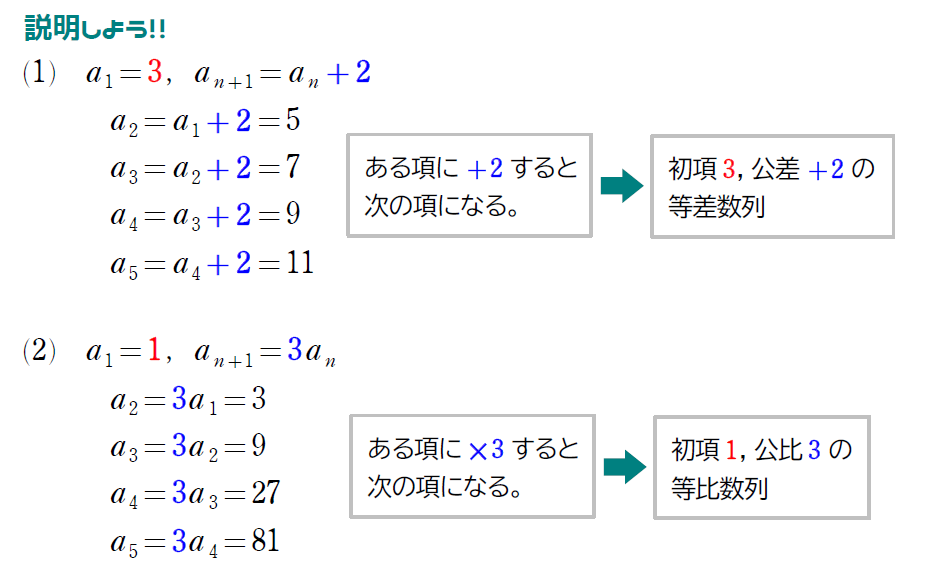
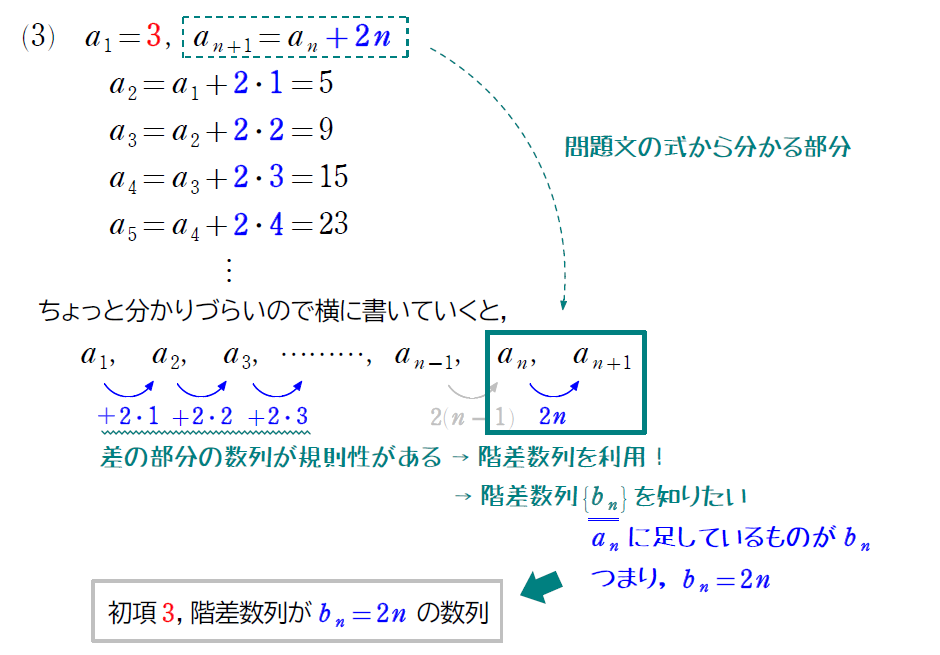
今の練習問題から公式を作っておきましょう!

今紹介した漸化式の型は今後よく利用するので、すぐに判断できるようにしましょう。
漸化式の問題を解こう!
等差数列型、等比数列型、階差数列型ってナニ?
先ほど紹介した公式を利用する問題を紹介します。


これら3つの漸化式に限らず、漸化式の問題は与えられた漸化式が何の型なのかを判断できるかが重要です。式の形の違いをしっかりと把握しておきましょう!
特性方程式型ってナニ?
『特性方程式とは…?』という話をしていくためにも、次の問題を見てみましょう!
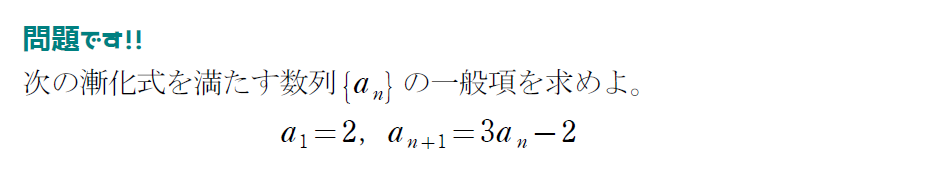




念のため、例題を通してもう一度解法を確認しましょう。
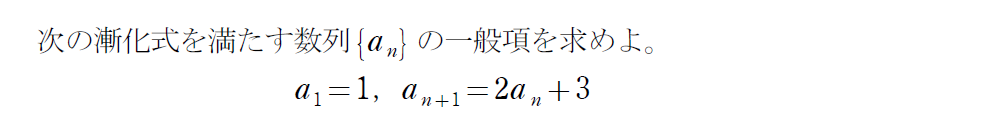


\(\small a_{n+1} =pa_n+q^{n+α} \)型ってナニ?
例題を参考に見ていきましょう。
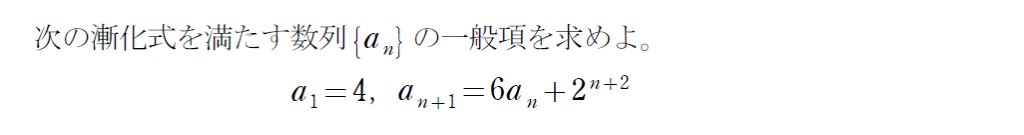



まとめ!
漸化式は一つひとつのパターンをしっかりと解けるようにしていくことが重要です。というのもこれから習っていく漸化式は、これまで習った漸化式を利用する問題もあります。型の違いなども確認しつつ、しっかりと復習してください。





コメント