こんにちは。ねこの数式のnanakoです。
今回は漸化式の応用問題の紹介です。特に隣接三項間漸化式の問題は確実にできるようにしておきたい問題となります!頑張っていきましょう!
今までの復習はこちらを利用してください。
分かりやすい【数列②】シグマを解説!公式の証明も紹介するよ。
分かりやすい【数列③】部分分数分解、等差×等比などいろいろな数列の和を解説!
分かりやすい【数列⑤】特性方程式などを利用する漸化式を紹介!
漸化式の応用問題!
どの漸化式の型も知らないと手も足も出ないものばかりなので、それぞれの型に合わせた解き方をしっかりと覚えておきましょう!
分数型ってナニ?
分数型は他の型との区別は簡単で、分母に \(\small a_n \) があったら、この型だと思ってください。
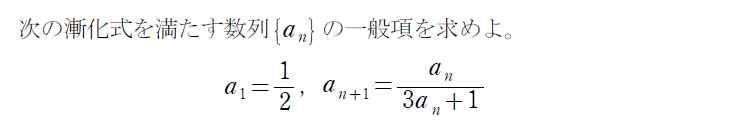


上の解答の「帰納的に」の部分は、きちんと示す場合は「数学的帰納法」というものを用います。こちらの紹介はまた別の記事で行います。
\(\small a_{n+1} = pa_n+an+b \)型ってナニ?
この型は解法がいくつかあります。1個目以外は見覚えがあるくらいでOKです!
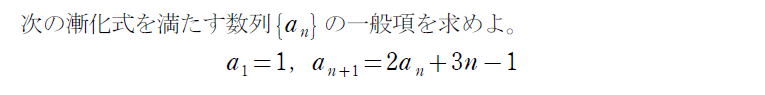



隣接三項間漸化式ってナニ?
何かの必殺技みたいな漸化式ですが、他の型との比較は簡単です。
\(\small a_{n+1} \) と \(\small a_{n} \) だけでなく、\(\small a_{n+2} \) も含まれている漸化式です。
解くためには公式が必要です!

上式の2次方程式も特性方程式と言います。2次方程式の解はどちらがαで、どちらがβでもかまいません。
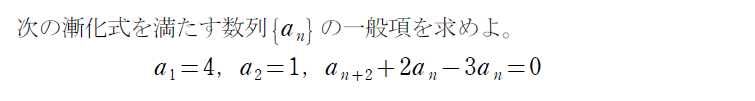

ちなみに異なる2つの虚数解のときも上の解き方で解けます。
次は重解の場合を体験してみましょう!
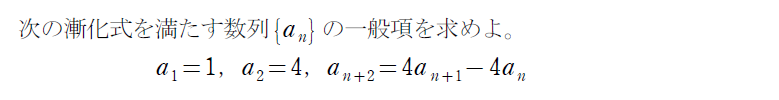

ちなみに重解じゃないときもαとβを入れ替えずに解き進めることは可能です!
漸化式の連立ってナニ?
2つの数列を組み合わせた漸化式です。
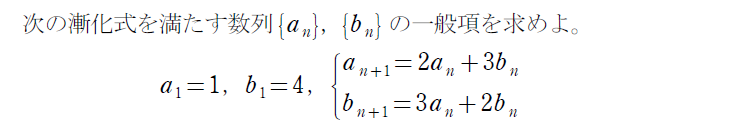



続いては、対称性が無い問題を見てみましょう。
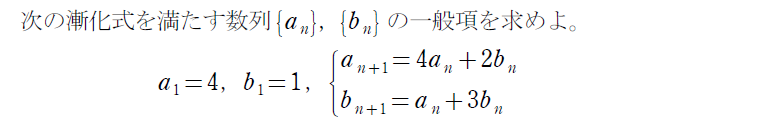


まとめ!
難しい問題も含まれていましたが、大丈夫でしたか?\(\small n \)番目と\(\small n+1 \)番目の対応が分かっていないと、さっぱり分からない…なんてことも。よく分からなくなってしまったら、特性方程式型などの仕組みを復習してみましょう。




コメント