こんにちは。ねこの数式のnanakoです。
今回は、数Ⅱ三角関数の公式と公式の使い方を中心に紹介したいと思います。
三角関数の基本の確認はこちらの記事から
三角関数の値の覚え方はこちらの動画を参考にしてください！！
加法定理，２倍角・半角の公式！
加法定理ってナニ？
まずはこちら！
\(\small \sin(60°+30°)≠\sin60°+\sin30° \)
イコールが成り立たないのは大丈夫ですか？
左辺は \(\small \sin90°=1 \) となりますが、右辺は \(\small \displaystyle \frac{\sqrt{3}}{2}+\frac{1}{2} \) となりますね。
なので、\(\small \sin \) の部分をカッコの中に分配・・・なんていう計算はできないので気をつけましょう。
ただ、これから三角関数を学ぶ上で上の計算のような分配をしたいシーンが度々出てきます。そのような時に利用するのが加法定理というものです。
証明は④③②①⑤⑥の順でいきましょう！！
それにしても、公式が多くて覚えるの大変そうですよね。有名な覚え方などを紹介しておきたいと思います。
公式の左辺の\(\small \, \alpha \, \) と \(\small \, \beta \, \)の間がマイナスのときは、右辺の符号が反転すると覚えてください。
では、さっそく加法定理を利用した問題を見ていきましょう。
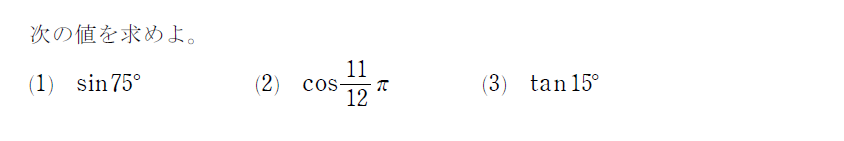
公式を覚える上でも類題の演習をしっかりとしておきましょう。
続いても加法定理を利用する問題です。
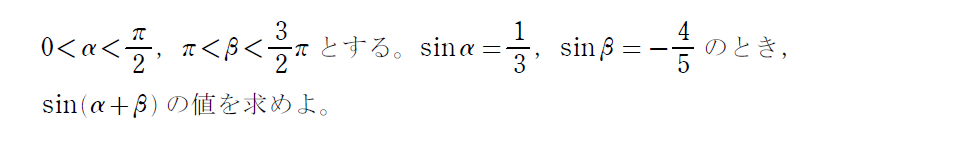
２倍角・半角の公式ってナニ？
続いては２倍角の公式・半角の公式の紹介です。その名の通り、公式の左辺が \(\small \theta \) の２倍・半分となっているものです。
２倍角の公式は丸暗記するというよりは、自分で証明するようなイメージの方が覚えやすいと思います。（半角の公式は丸暗記でもOKです。）
ポイントは（３）と（４）ですね。（３）で合っていても（４）が違った人がいるのでは？
この問題で重要なのは角度の範囲です。\(\small \alpha \) の範囲と \(\small \displaystyle \frac{\alpha}{2} \) の範囲をごっちゃにしてしまっているのが原因です。
これからの三角関数で重要なポイントとなるのでしっかりと抑えておきましょう。
３倍角の公式ってナニ？
続いては３倍角の公式の紹介です。
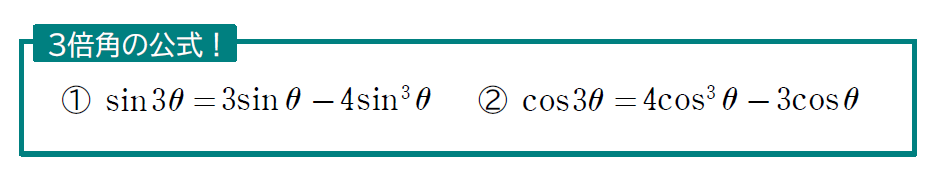
３倍角の公式を利用する問題は色々ありますが、今回は公式の証明を例題とします。３倍角の公式の証明は入試でも出題されることが多いので経験しておいて損はありません。
積和・和積の公式！
続いては積和・和積の公式です。この公式は定期テストでは応用問題での使用となります。
この記事では公式の紹介？証明？覚え方にとどめておきます。利用の仕方については今後の記事で紹介したいと思います。
積和・和積の公式はとにかく覚えづらい公式です。丸暗記できそうなら、それでもかまいませんが、自分で作ることをお勧めします。
積和の公式ってナニ？
積和の公式とはその名の通り、三角関数の積の形から三角関数の和の形に変形するための公式です。
では、さっそく作り方をみてみましょう！
上の方法で②～④の公式を自分で作ってみましょう。一応、下に証明を載せておくので、答え合わせに使ってください。
大丈夫でしたか？実践問題の際にパパっと作れるように何度か練習しておきましょう。
和積の公式ってナニ？
続いての和積の公式も自分で作りましょう。
「作りましょう。」とは言ったものの、積和の公式よりは『暗記要素』が含まれています。
他の公式も作ってみて下さ～い。
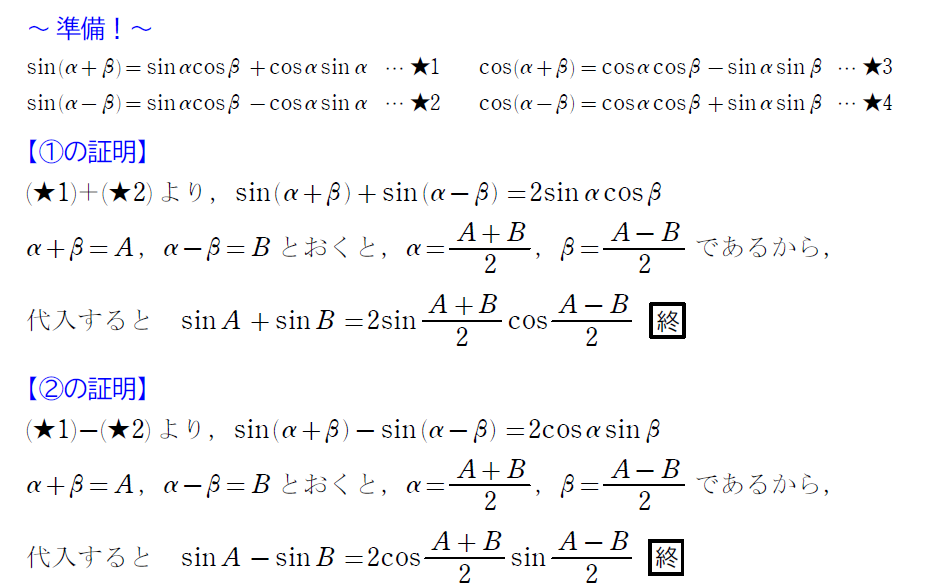
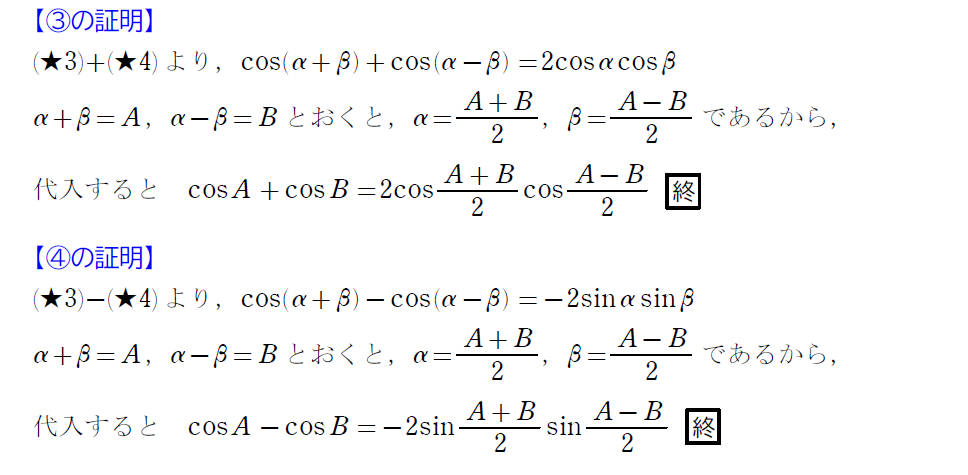
まとめ！
今回は公式の紹介が中心でした。これらの公式は色々な問題で利用するのでしっかりと確認しておきましょう。
コメント
和積の公式の
sinA-sinBの欄
が間違っています
ありがとうございます。修正いたしました。
三角関数の加法定理！と書かれた画像でαとβを間違っていると思われます。
ありがとうございます。修正しました！