こんにちは。ねこの数式のnanakoです。
今回は、場合の数・確率の順列と組合せを紹介していきます。
この単元は、高校数学の中でも1,2を争うくらい苦手な人が出やすい単元です。
というのも、問題をパターン化しようとすると、
「パターンが多い」and「パターンの区別が難しい」
ので、ちゃんと理解していないとすぐにすべての内容が分からない状況になります。
一つひとつの内容をしっかりと理解し、違いを把握しながら進めましょう!
順列を紹介!
順列とは、「区別可能な特定の元から有限個を選んで作られる重複の無いを有限列」・・・なんのこっちゃ。
順列を簡単に説明すると、区別のつく何個かのものを1列に並べたものです。例えば・・・
A,B,C の3人を一列に並べるのは『ABC、ACB、BAC、BCA、CAB、CBA』の順があります。これらの列のことを順列といいます。
辞書式配列と樹形図ってナニ?
辞書式配列と樹形図というのを中学校のときに習ったのを覚えていますか?
辞書式配列というのは、アルファベットを並べる際に辞書に出てくる順に書き出していく方法です。
例えば、先程の「A,B,C の3人を一列に並べる方法」では、『ABC、ACB、BAC、BCA、CAB、CBA』の6通りが答えでした。
辞書では、A□□,B□□,C□□は『A□□』が一番最初に載っています。次に、AB□とAC□では、『AB□』の方が先に載っています。
そのため、辞書式配列では、最初に書き出すのは『ABC』、次に書き出すのは『ACB』、その次が『BAC』といった順で書き出すことになります。
続いては、樹形図を復習しましょう。「A,B,C,D の4人を一列に並べる方法」を例にみていきましょう。
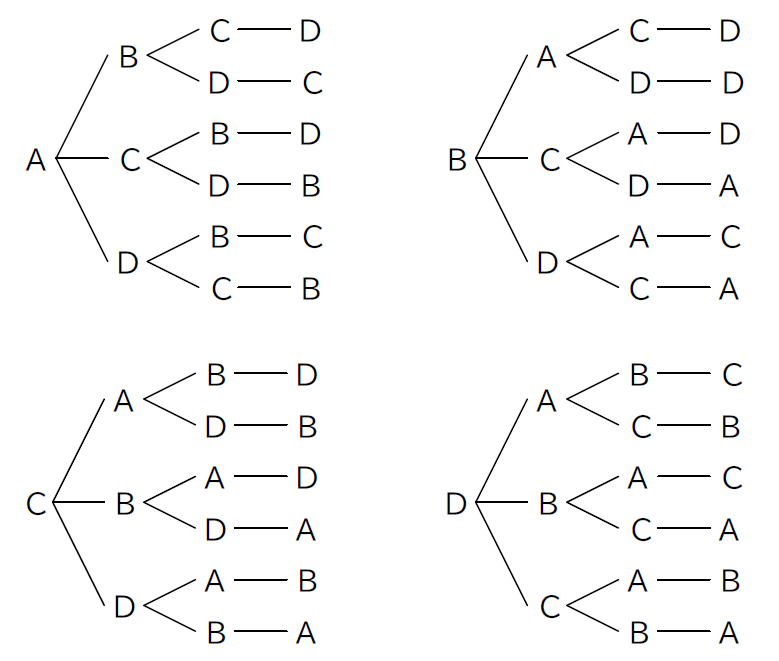
図のように、枝分かれさせて並び順などを表現するものを樹形図と言います。ここで書き出すときに辞書式配列を意識すると、書きそびれが減るので意識しましょう。
\(\small {}_n \mathrm{P}_r \)ってナニ?
さきほど「A,B,C,D の4人を一列に並べる方法」が何通りか求める際、樹形図を利用しました。
ただ、これから学習する問題では登場する人数が増えたりするので、樹形図を書くのが困難となります。そこで樹形図を利用せず、計算で求めることを考えてみましょう。
「A,B,C,D,E の5人から3人を選んで一列に並べる方法」を例にみていきましょう。
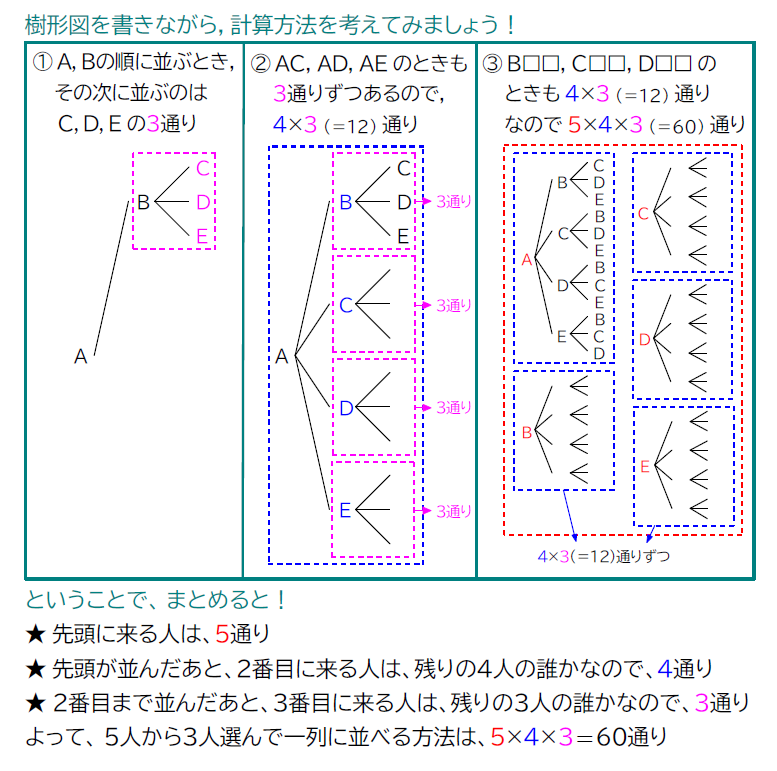
同じように求めてみましょう!
次の問いに答えよ。
(1) 6人の中から2人を選び,一列に並べる方法は何通りか。
(2) 7人の中から3人を選び,一列に並べる方法は何通りか。
(3) 5人を一列に並べる方法は何通りか。
(1)
最初に並ぶ人は6通り,次に並ぶのは残りの5人の誰かなので5通りなので,
求める場合の数は,\(\small 6 \times 5 = 30 \) 通り
(2)
最初に並ぶ人は7通り,2番目の人は6通り,3番目の人は5通りなので,
求める場合の数は,\(\small 7 \times 6 \times 5 = 210 \) 通り
(3)
1番目, 2番目, 3番目, 4番目, 5番目には,それぞれ5通り, 4通り, 3通り, 2通り, 1通りが考えられるので,
求める場合の数は,\(\small 5 \times 4 \times 3 \times 2 \times 1 = 120 \) 通り
さて、本題の \(\small {}_n \mathrm{P}_r \) の紹介をしていきましょう!
まずは、さきほどの例題1(2)の問題を例に見ていきます。

ちなみに『5!』は『5の階乗』と読みます。授業などで『5ビックリ』と読んでしまうとかなり恥ずかしいので気をつけてくださいね。(昔、実際に生徒でいました、笑)
これらを公式化してみましょう。


さて、ここまでは大丈夫だったでしょうか?
続いては、0! と \(\small {}_n \mathrm{P}_0 \) の説明をしていきましょう。
どちらの値も1となりますが、0になると思った人もいるんじゃないですかね?
\(\small 0! \) は0から1までの整数をかける? たぶん0かな?
\(\small {}_n \mathrm{P}_0 \) は \(\small n \) から 0 個の整数をかける? 0?それとも1?
いろんな解釈でいろんな値になりそうですが、この2つの値は『求める』というわけではなく、定義として『決まっている』ものです。なぜ、そう決まったかは、単にそう決めてしまうと色々な計算で矛盾が生じなかったと考えましょう。
続いては実践的な公式を紹介していきたいと思います。

この公式は例題1の計算をふまえたものです。例題1の類題を公式を利用して求めてみましょう!
次の問いに答えよ。
(1) 6人の中から3人を選び,一列に並べる方法は何通りか。
(2) 7人の中から2人を選び,一列に並べる方法は何通りか。
(3) 4人を一列に並べる方法は何通りか。
(1) \(\small {}_6 \mathrm{P}_3 = 6 \cdot 5 \cdot 4 = 120\) 通り
(2) \(\small {}_7 \mathrm{P}_2 = 7 \cdot 6 = 42\) 通り
(3) \(\small 4!= 4 \cdot 3 \cdot 2 \cdot 1 = 24 \) 通り
\(\small 4! \) などの値は今後よく利用します。
毎回計算するのは大変なので、ある程度は覚えてしまう人がほとんどです。

ポイントはピンクの部分です。\(\small 5!=120 \) くらいまでは覚えてしまう人が多いと思いますが、\(\small 6! \) 以降は覚えるか微妙なラインです。
でも、覚えていないと \(\small 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \) をまともにかけ算することになり、微妙に時間がかかります。なので、\(\small 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 =5! \) であることを利用して、\(\small 6 \times 5! = 6 \times 120 \)を計算すると楽に求めることができます。
ちなみに、 \(\small 7! \) は \(\small 7 \times 6! \) を計算します。もし、\(\small 6!=720 \) を覚えているなら、\(\small 7 \times 720 \) を計算すれば良いですが、\(\small 6!=720 \) を覚えていない場合は、先に \(\small 6! = 6 \times 5! = 6 \times 120 \) を計算してから、\(\small 7!\) を計算しましょう。
先ほどは公式を利用するだけで解ける問題でしたが、実戦的な問題も見ていきたいと思います。
でも、その前に言わせてください!!
ここから、数A場合の数・確率で一番重要なポイントです!!!
次の例題で紹介する考え方は、これから学習していく「場合の数・確率」のほとんどの問題で利用します。
なので、絶対に流し見ないように気をつけてください!!
A,B,C,D,E,F の合計6人を一列に並べるとき、次の場合の数を求めよ。
(1) 総数
(2) A,B,C の3人が隣り合う
(3) A,B が隣り合わない
(4) A,B,C のうち、どの2人も隣り合わない
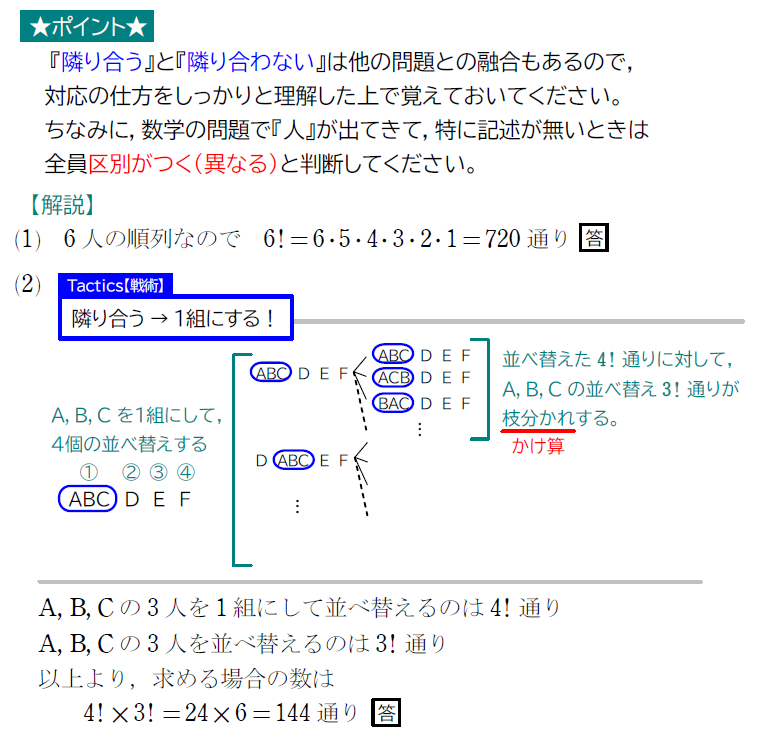
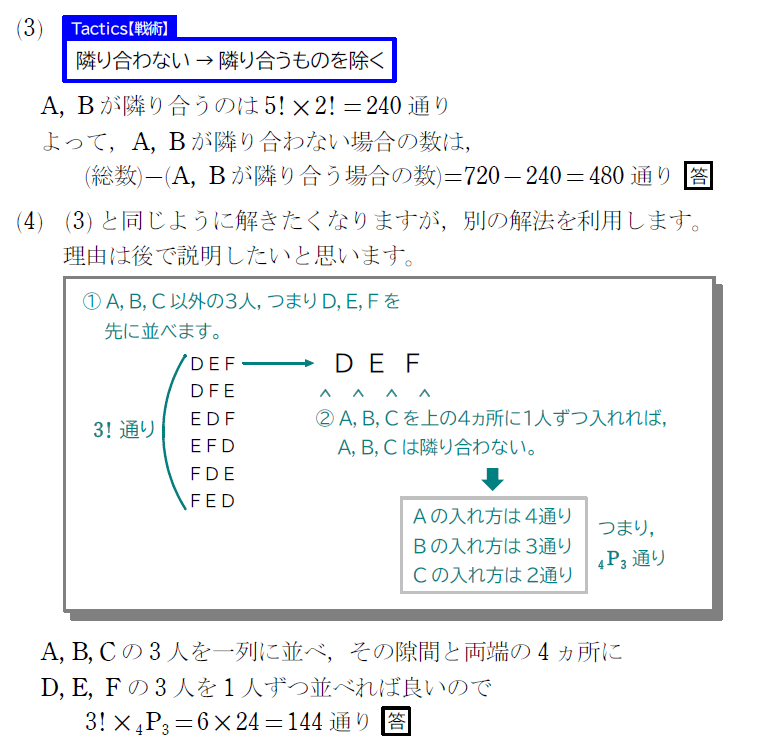
(3)と(4)では同じ『隣り合わない』という問題でしたが、違う考え方を利用しました。
そして、この2つの考え方が、今後の場合の数・確率のほとんどの問題に関わってくるものとなります。

さて、それとは別になぜ(3)と(4)では違う考え方を利用したのでしょうか?
まず、(3)の問題から見直します。実はこの(3)は、(4)の考え方 つまり 不要なものが含まれないように数えることができます。
先に、A,B以外の4人を先に並べ、A,Bを隙間と両端の5か所に1人ずつ入れていくことを考えると、
\(\small 4! \times {}_5 \mathrm{P}_2 = 24 \times 20 =480\) 通り
このように同じ答えとなりました。では、(4)の問題はどうでしょうか?
(総数)\(\small – \)(隣り合う)\(\small =720-144=576 \) 通り
(4)の\(\small 144 \) 通りと一致しませんね。なぜでしょう???
実は「隣り合う人数」がポイントです。
先ほどの\(\small 576\) 通りは、「(総数)\(\small – \)(A,B,C の3人が隣り合う)」を計算したものです。
(4)は「A,B,C のうち、どの2人も隣り合わない」という問題でした。どうでしょう?気づきますか?
さきほどの「(総数)\(\small – \)(A,B,C の3人が隣り合う)」を計算したものは、
「(A,B,C のうち、どの2人も隣り合わない)+(A,B,C のうち、2人だけが隣り合う)」
となってしまいます。つまり、「A,B,C のうち、2人だけが隣り合う」も含まれていたのが原因でした。まとめると、
〇桁の整数を作る問題ってナニ?
さて、続いては〇桁の整数シリーズです。
0,1,2,3,4,5 の6個の数字から重複を許さず3個を選び1列に並べ3桁の整数を作るとき、次の条件を満たすものは何個あるか求めよ。
(1) 総数
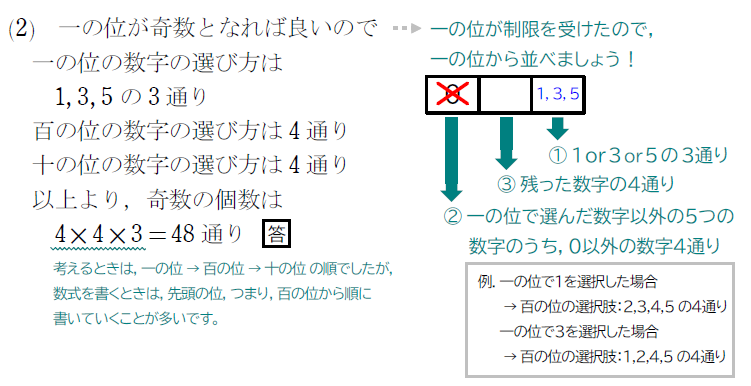
(2) 奇数
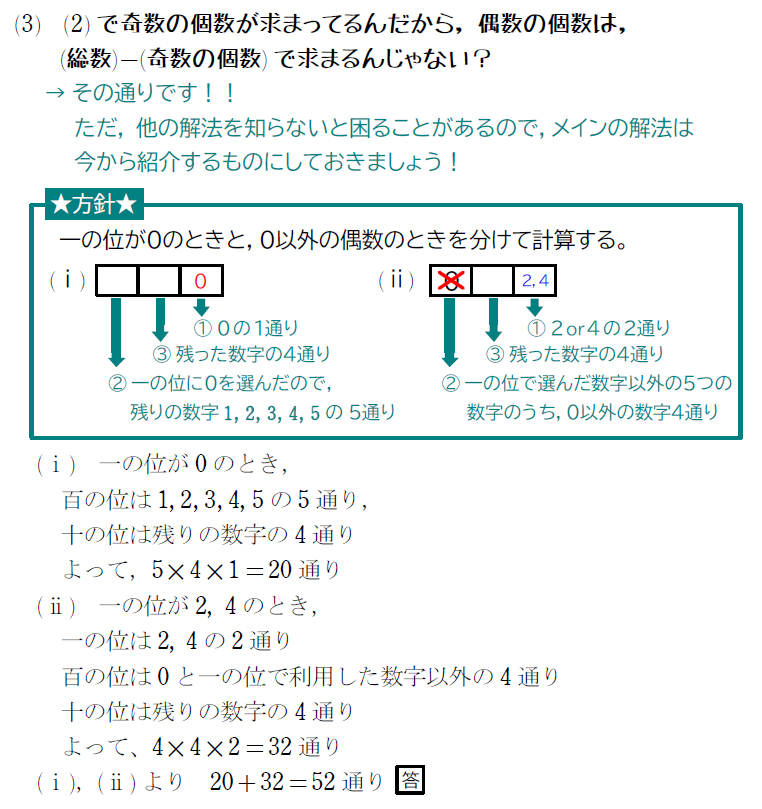
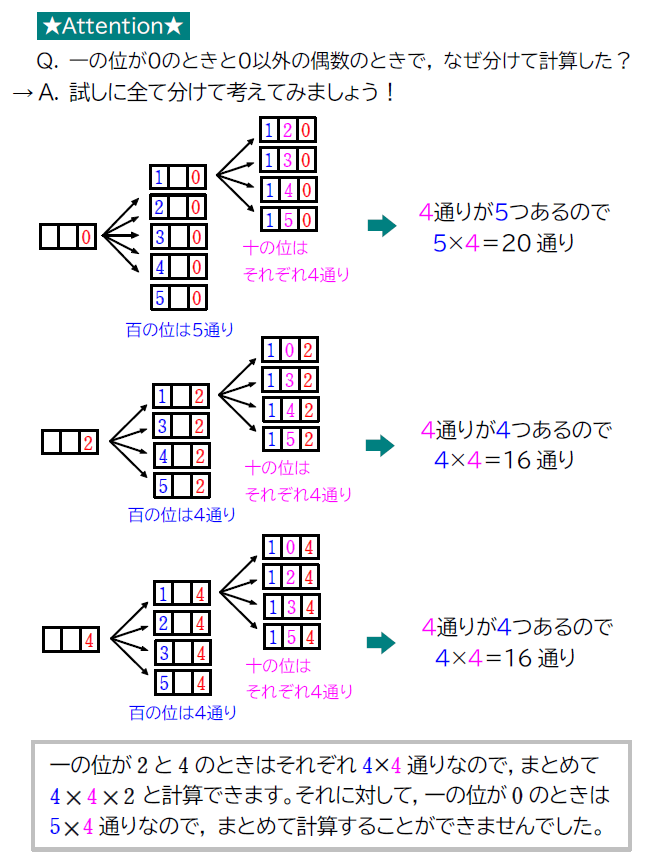
(3) 偶数
(4) 3の倍数
(5) 9の倍数
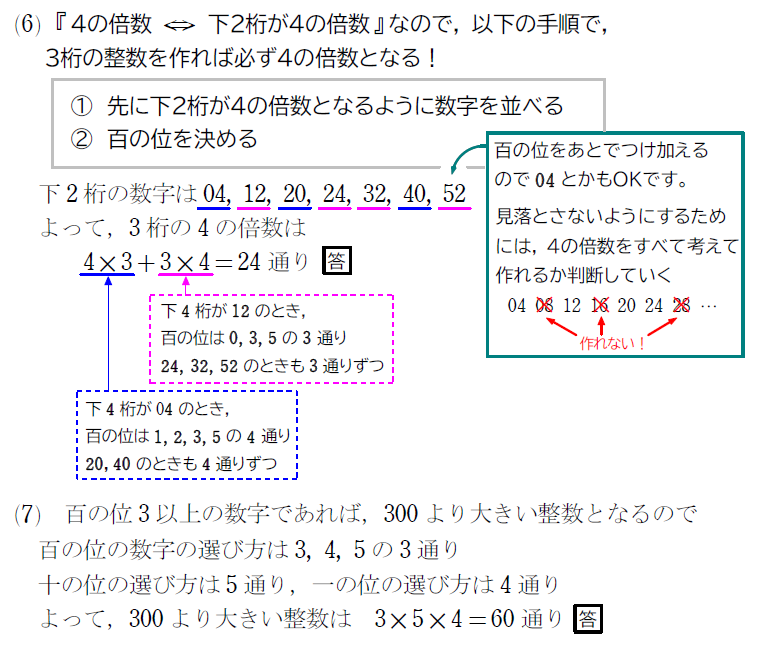
(6) 4の倍数
(7) 300 より大きい
さて、今回の問題の一番のポイントは最高位の位(この問題では百の位)です。
問題文では3桁という指定があります。なので、0,3,1の順に並べた 031 は3桁整数とは呼べないのでNGです。


「〇の倍数」シリーズは、さきほどの例題の問題以外に、5の倍数、6の倍数などが出てきます。
5の倍数は一の位が0のときと、5のときで分けて計算していきます。
6の倍数は「3の倍数」かつ「偶数」と考えて解いていきます。
円順列・数珠順列を紹介!
円順列ってナニ?
続いては円順列を見ていきましょう。
『円順列』とは円を並べるわけではなく、円形に並べていくことを言います。
ここでも、例題3で紹介した2つの考え方を利用していきます。
まずは、下の絵を見てください。

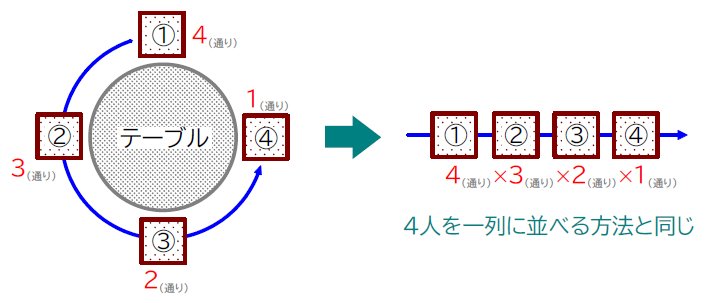
席が4つあります。この席に4人を座らせる方法が何通りあるか求めましょう。
下の図の①②③④の順に座らせることを考えてみます。

このとき、4人を一列に並べる方法と同じなので、 \(\small 4!=24 \) 通りになります。
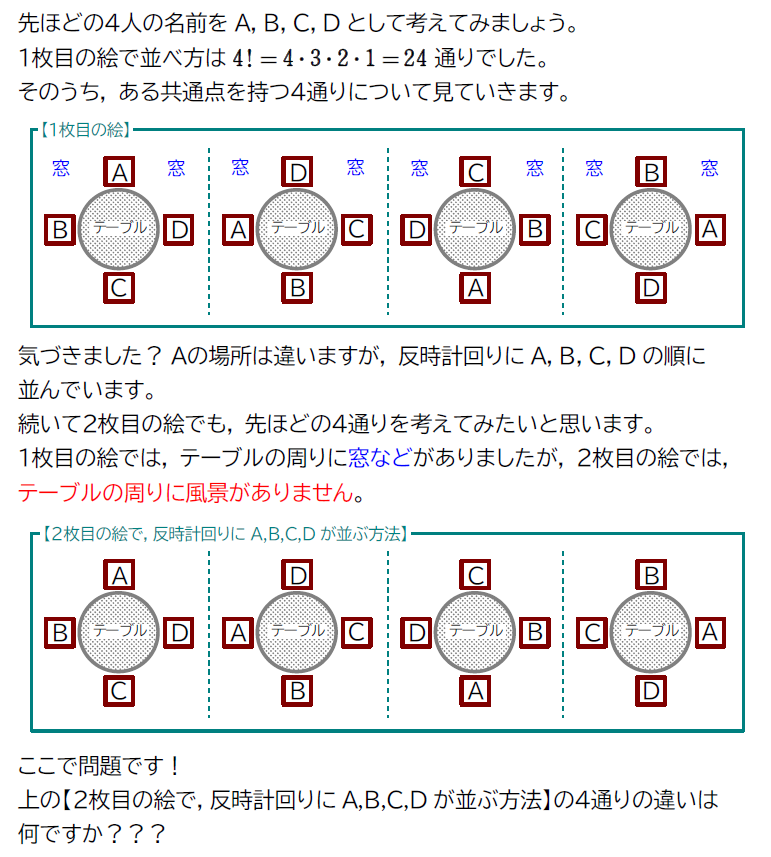
では、次のような座席ではどうでしょうか?

さっきと同じでしょ!って思った人が多いと思いますが、違うんです!!
詳しく見ていきましょう!
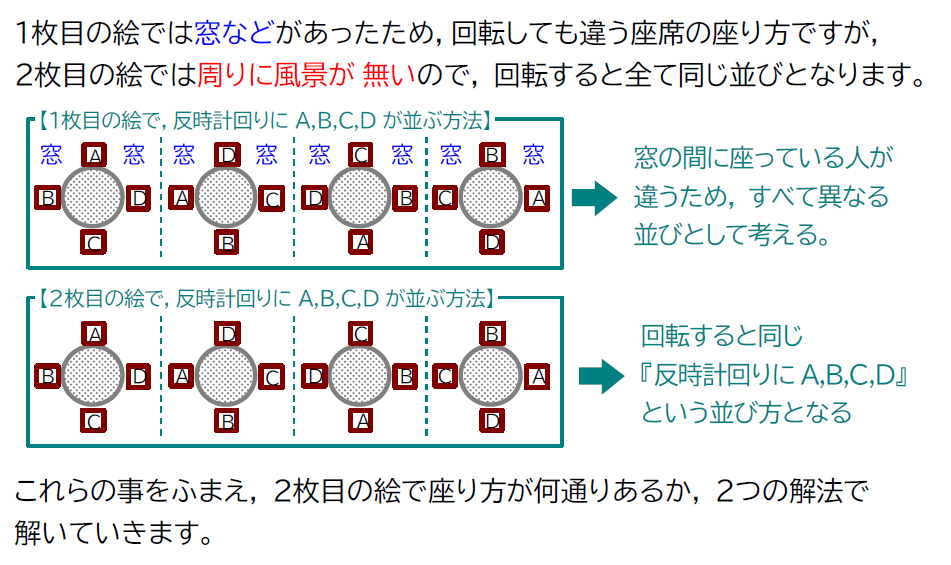
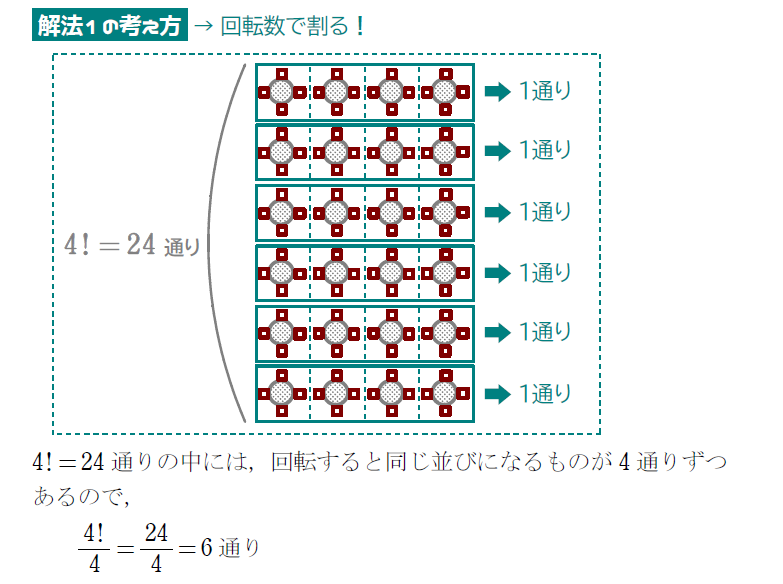
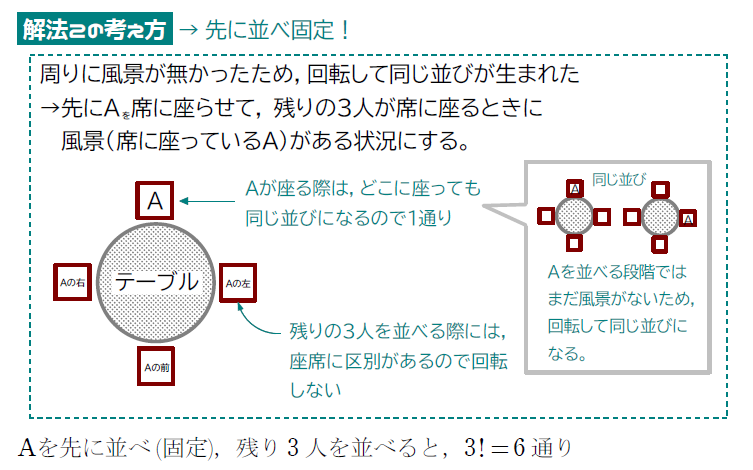

上で紹介した考え方は、これからの問題でも使うのでしっかりと理解しておきましょう。
では、上の内容を踏まえて、円順列の公式を紹介します。

問題を解く際、基本的には解法2の考え方(固定)を利用して考えていくと解きやすいことが多いです。
では、公式を利用した問題を見てみましょう。ただ公式を利用するだけだと、解けないことが多いので注意してくださいね!
教師2人、男子生徒3人、女子生徒3人の計8人を円形に並べるとき、次のような並びは何通りあるか求めよ。
(1) 総数
(2) 教師2人が隣り合う
(3) 教師2人が隣り合わない
(4) どの男子生徒も隣り合わない
(5) 2人の教師が向かい合う
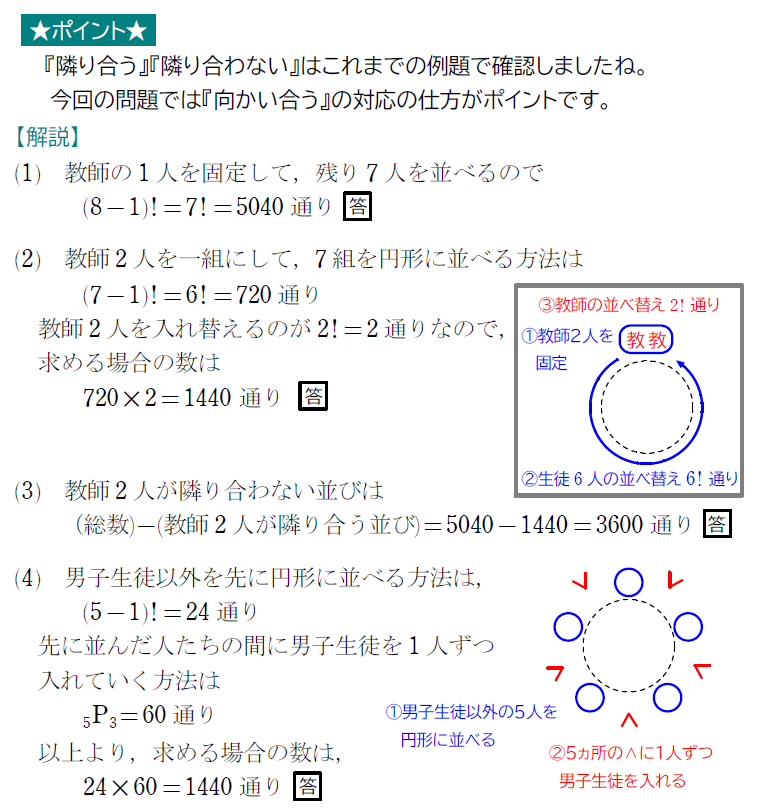
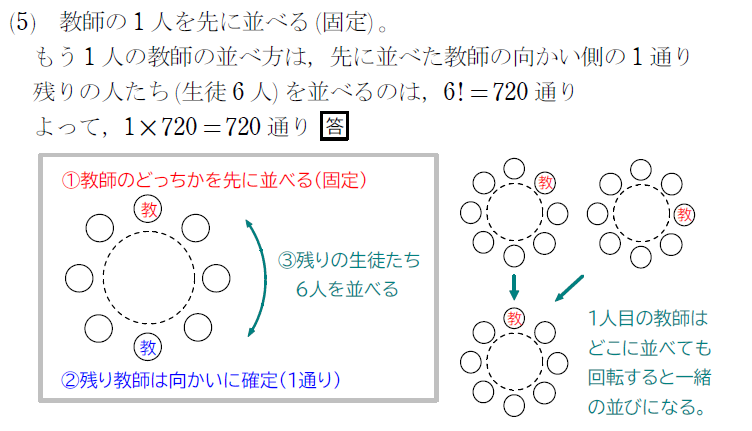
円順列でも隣り合わない問題は、人数によって使い分けてください。
数珠順列ってナニ?
数珠順列とは、数珠やネックレスなどを作ったものを言います。円順列との違いは表裏が無いことです。つまり、ひっくり返すことができる点です。
赤、青、黄、緑の4色の玉にひもを通してネックレスを作るとき、何通りできるか考えてみましょう。
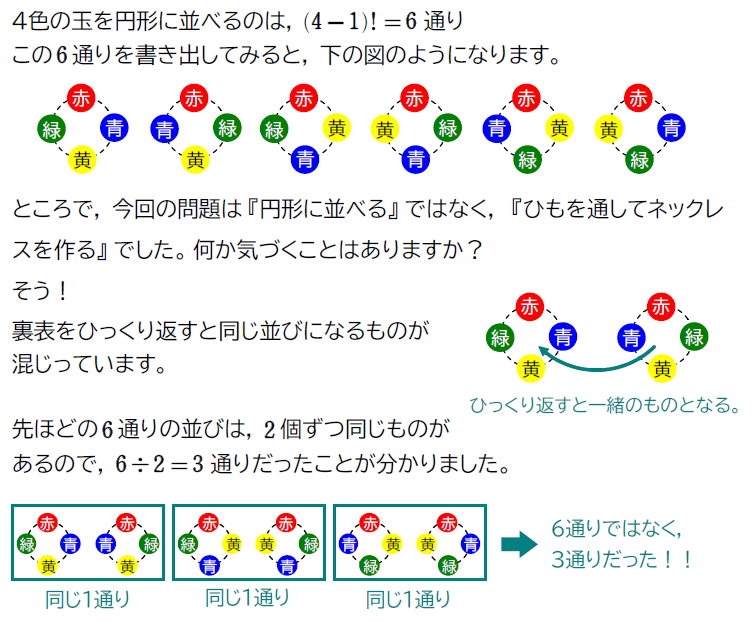
では、公式化しておきましょう!

上下に区別が無い状態で、円形に並べる際には2で割ると覚えておきましょう!
まとめ!
順列の問題はいかがでしたか?
一つひとつの例題をしっかりと理解することはもちろん、それぞれの問題の違いを比較することが重要です。次の内容に入る前にしっかりと復習しおきましょう。




コメント