こんにちは。ねこの数式のnanakoです。
今回は『組合せ』と『同じものを含む順列』を紹介していきたいと思います。
順列や円順列などで学習した内容も関わってきます。心配な人は下の記事で復習しておきましょう。
組合せを紹介!
組合せってナニ?
『組合せ』とは言葉の通り、選んできたものの組合せを意味します。
さっそくですが、例を見てみましょう!
例.A, B, C, D, E の5人から3人を選ぶ方法は何通りあるか求めよ。
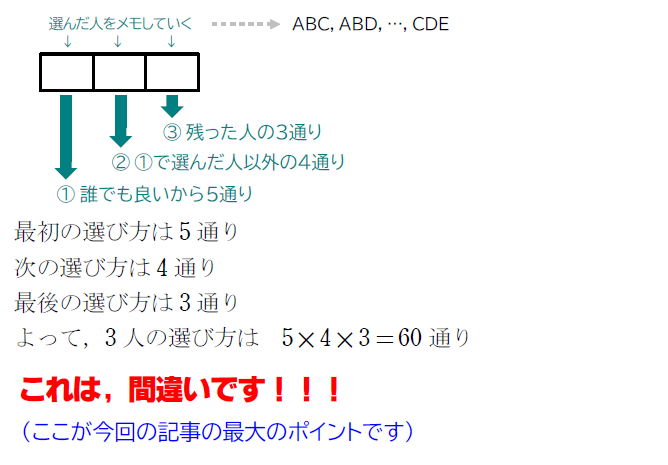


では、これを公式化してみましょう!!




実際の問題で使い方を見ていきましょう。
男子4人,女子3人の中から4人を選ぶ。次の問いに答えよ。
(1) 選び方の総数を答えよ。
(2) 男女2人ずつ選ぶ方法が何通りか答えよ。
(3) 女子を少なくとも1人選ぶ方法が何通りか答えよ。

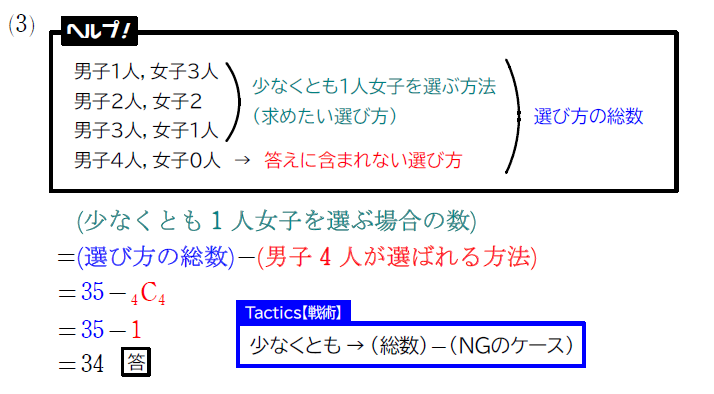
(2)で\(\small \, {}_4 \mathrm{C}_2 \, \)と\(\small \, {}_3 \mathrm{C}_2 \, \) をかけ算しました。今後も同じようなシチュエーションでかけ算を利用するので押さえておきましょう。
また、(3)でのポイント『少なくとも』もよく利用するので覚えておきましょう。
グループ分けってナニ?
さて、続いてはグループ分け問題です。仕組みが重要ですよ!
今後出てくる他の例題との違いも重要となってきます。問題文の少しの違いで、まったく違う解答になるので違いをしっかりと確認しましょう!
次の問いに答えよ。
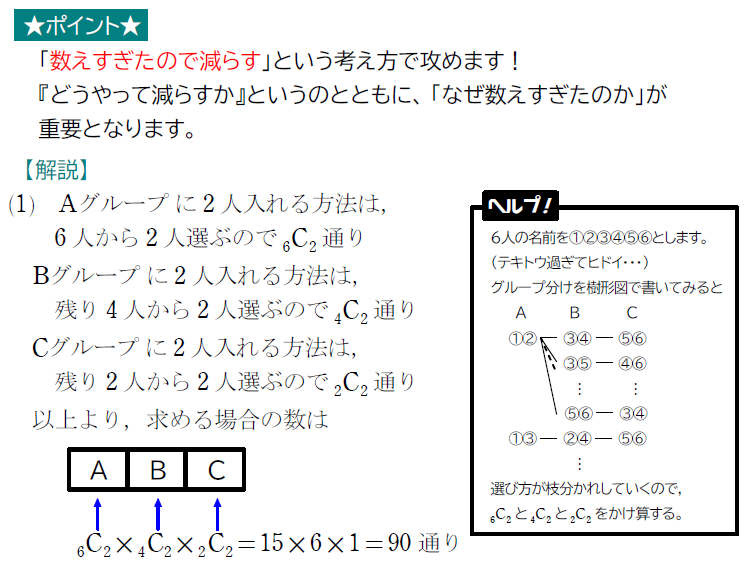
(1) 6人を2人ずつの3グループA,B,Cに分ける方法が何通りあるか答えよ。
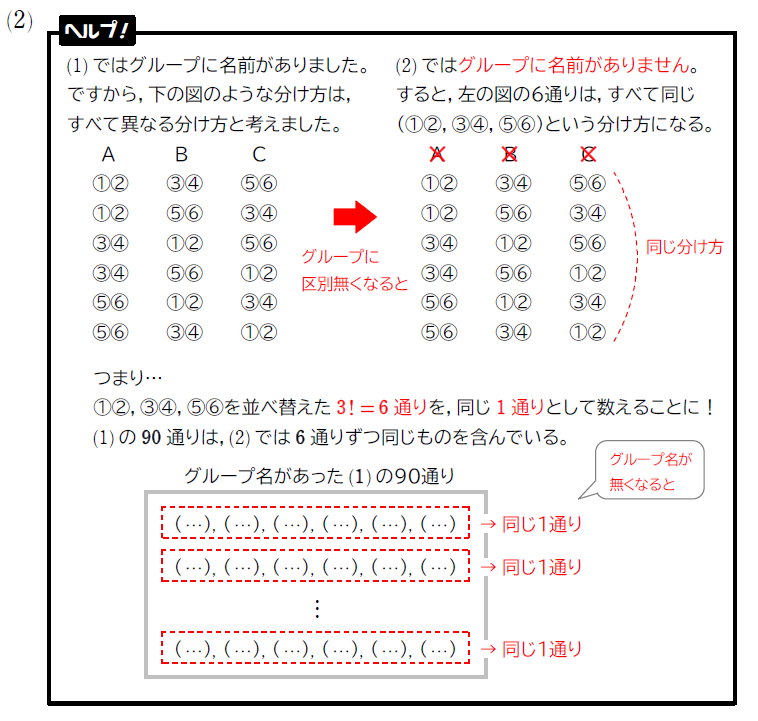
(2) 6人を2人ずつの3グループに分ける方法が何通りあるか答えよ。
(3) 9人を4人,3人,2人の3グループに分ける方法が何通りあるか答えよ。
(4) 8人を3人,3人,2人の3グループに分ける方法が何通りあるか答えよ。



重複順列を紹介!
重複ってナニ? なぜにいまさら順列?
という声が聞こえてきそうですね。重複というのは「同じものを選んで良い」という意味です。
つまり、重複順列は,同じものを何度も利用しても良いというルールで並べることです。
例.0,1,2,3,4の5つの数字の中から重複を許し3つの選び,3桁の整数を作る。
(1) 総数は何通りできるか。
(2) 偶数は何通りできるか。
1回利用した数字も再利用可能(もう一度選択肢に入る)なので、そこだけ考慮すれば楽勝です!
解説を見てみましょう。
(1) 百の位は0以外の4通り,十の位は5通り,一の位は5通り
以上より,求める場合の数は 4×5×5=100 通り
(2) 一の位は0または2または4なので3通り,
百の位は0以外の4通り,十の位は5通り
以上より,求める場合の数は 4×5×3=60通り
重複OKなので、(2)は一の位が0と0以外の偶数で場合分けしなくても良いのも,ポイントとして押さえておきましょう。
さて,重複順列でグループ分けの問題を見ていきましょう。

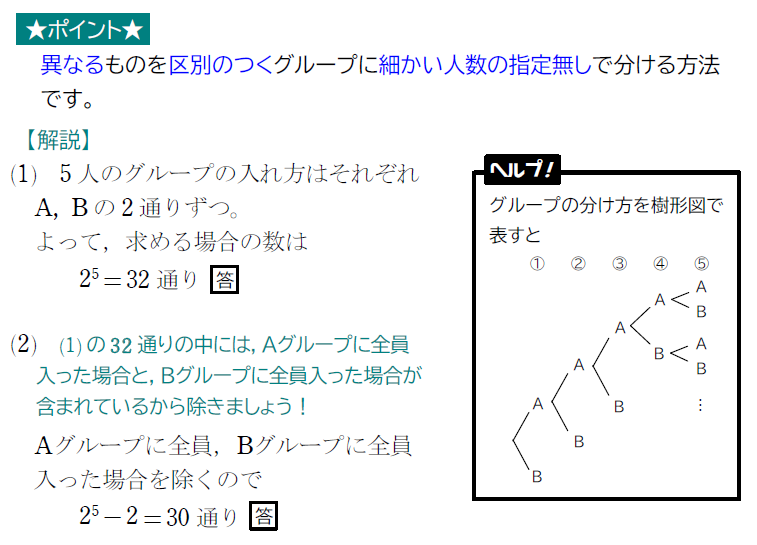

例題2との違いをしっかりと確認しておきましょう。
また、今後の例題との違いをはっきりするために確認しておきたいとのが、
『異なるものを区別がつくグループに分けている』という点です。
青い部分の設定が変わると求め方が変化するので気をつけましょう!
同じものを含む順列を紹介!
同じものを含むってナニ?
具体例から見ていきましょう!
例:A, A, Bの3文字を並べ替えるのは何通りあるか求めよ。
3文字を並べ替えるので、\(\small 3!=3 \cdot 2 \cdot 1 = 6 \, \)通り…が間違っているのは、分かりますか?
実際に書き出してみると、AAB,ABA,BAA の3通りしかないですね。
なぜ間違えてしまったかというと、2つのAは区別が無いのに区別があるものとして数えていたことが原因です。詳しく見てみましょう!




最短経路ってナニ?
さて、続いては『同じものを含む順列』を利用する問題の代表とも呼べる「最短経路」の問題を見ていきましょう。
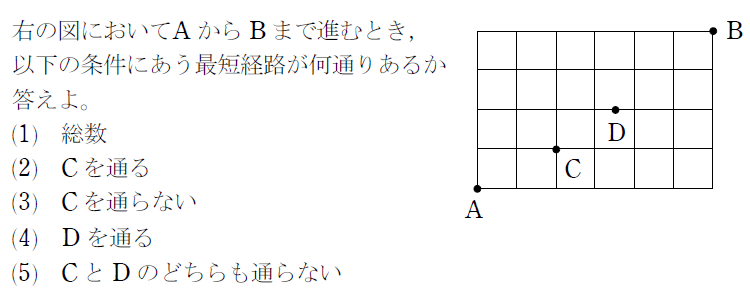
まずは問題を解く上での考え方を見ていきましょう!
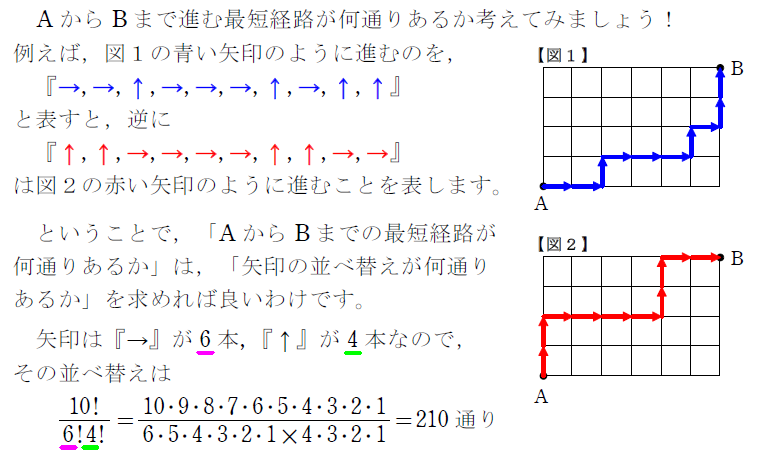

ということで,この考え方を利用して解答を見ていきましょう!!

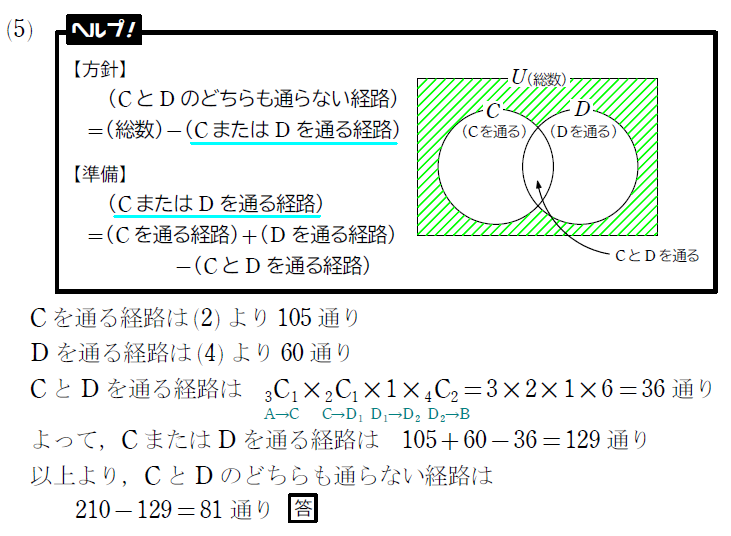
重複組合せを紹介!
重複順列は、同じものを繰り返し使うのを許して並べることでした。
重複組合せは、同じものを繰り返し使うのを許して組み合わせを作ることです…。
分かったような、分からなかったような…
具体例を見ていきましょう!
あるコンビニには、肉まん、あんまんの2種類の中華まんが売っています。どちらの中華まんも、それぞれ在庫は3個以上あります。この中から3個購入するとき、中華まんの選び方は何通りあるか?
まずは関西地方の方々へごめんなさい。肉まんは豚まんと表現すべきだったでしょうか?
さて、本題に入っていきましょう!
今回の中華まんの選び方は、「同じ種類の中華まんを何度も選んで良いので(重複を許し)3個選ぶ」という問題でした。このような選び方を重複組合せと言います。
では、計算で出す方法を考えてみましょう。

では、実際の例題を見ていきましょう!




まとめ!
それぞれの例題は理解できましたか?
一つひとつの例題をしっかりと理解出来たら、例題を比較して違いを確認していきましょう!
特に例題3と例題6の問題文の違いを確認して、なぜその解法じゃないといけないのか確認してください。





コメント