こんにちは。ねこの数式のnanakoです。
今回は、三角比 の 正弦定理、余弦定理、三角形の面積 を紹介していきたいと思います。これらの公式を紹介すると、何に使えるのかピンときていなかった三角比の値も頑張ってきて良かった!と思えます。
がんばりましょう!
ちなみに、三角比の値を覚えられていない人は、下の解説動画を確認してください!
正弦定理・余弦定理
三角形の辺の長さや頂点の角度を無性に調べたくなる日ってありますよね?(いや、無いでしょ・・・)
中学生のときは、どこに補助線を引くか悩みながら頑張っていたと思いますが、面倒くさくなかったですか?
三角比を利用すれば、面倒な補助線も引かずにパパっと公式で求める事ができます。
さっそく見ていきましょう!
正弦定理ってナニ?
正弦定理というのは、正弦 つまり sinθ を用いた公式のことで、三角形の辺の長さや角度、外接円の半径を求めたりすることに使います。
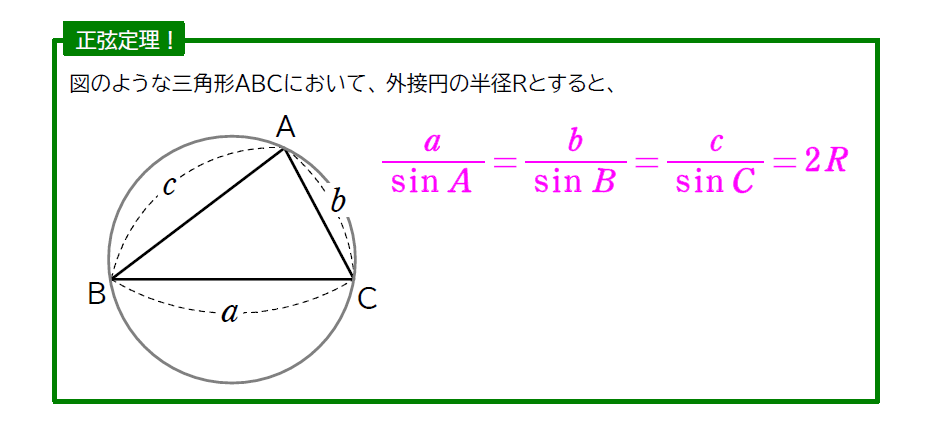
公式の覚え方は、向かい合う辺と角で分数を作っていくのがポイントです。
証明も一応、目を通しておきましょう。↓
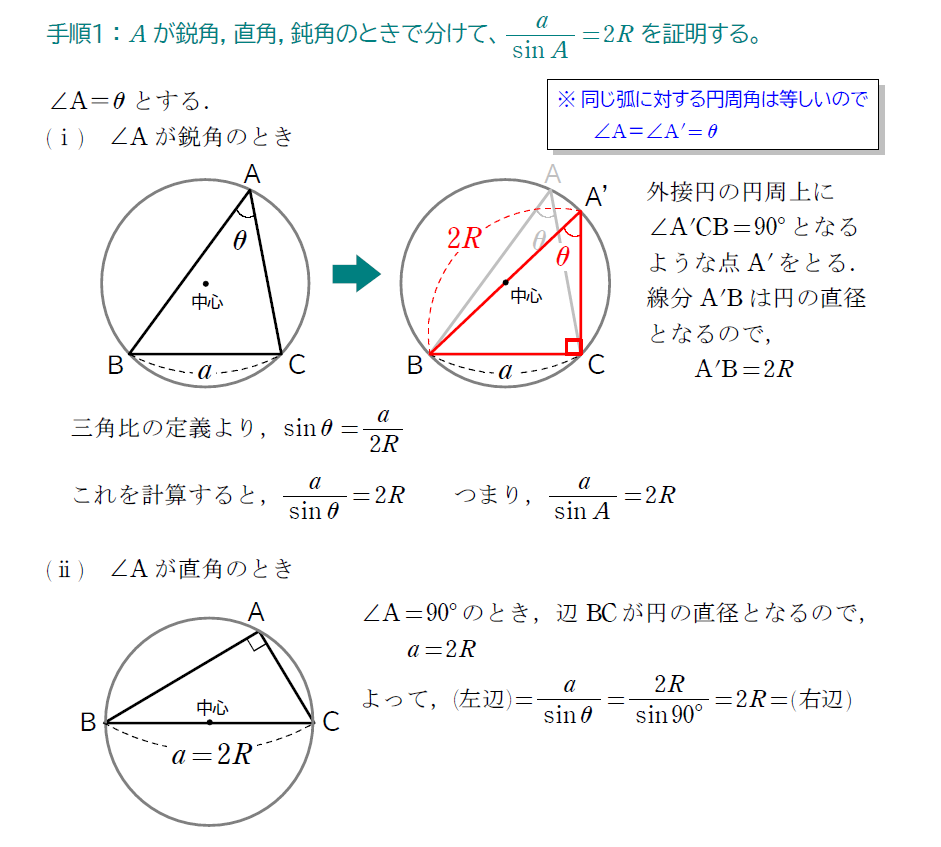
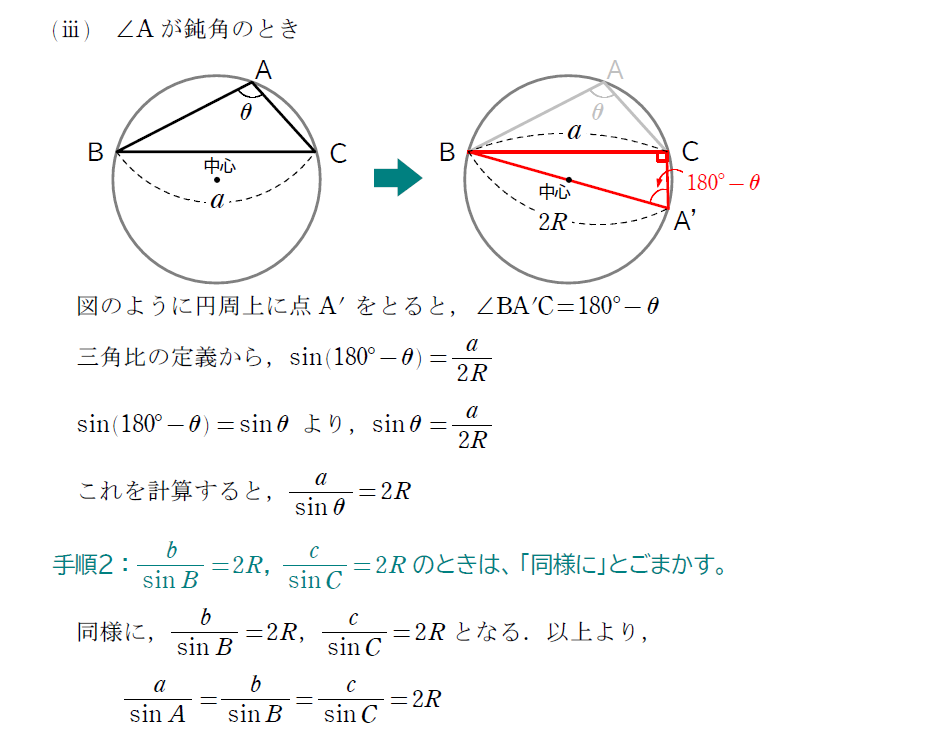
この正弦定理は、次に紹介する余弦定理とセットとなるような公式で、使い分けがポイントになります。実際の問題を通して見てみましょう。

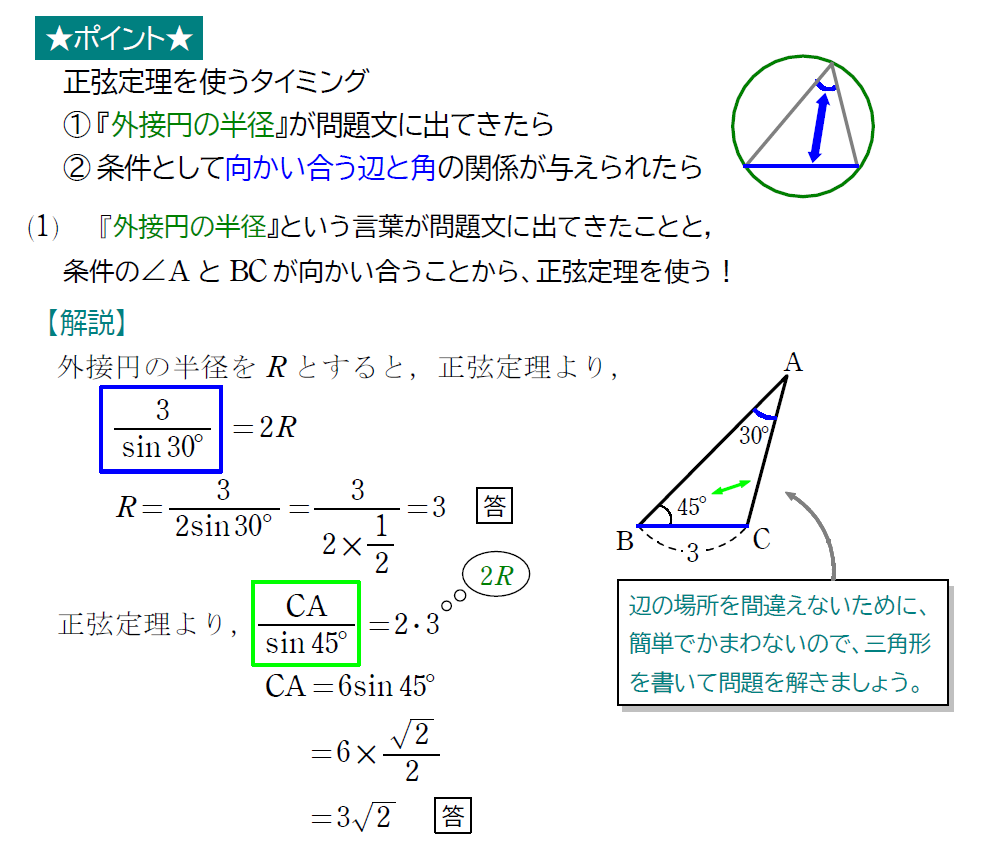
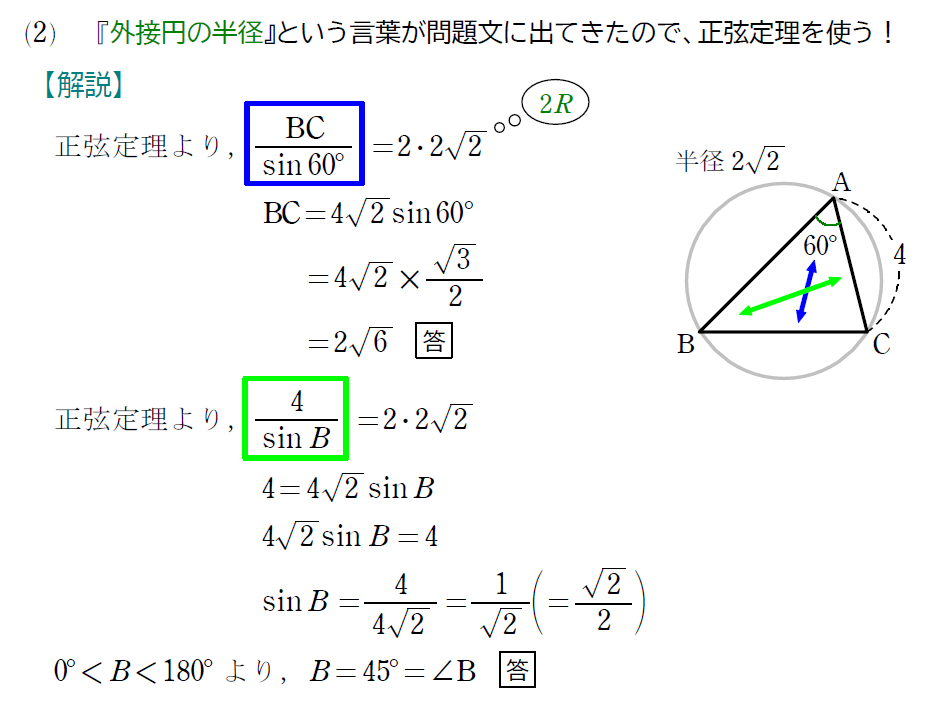
ということで、正弦定理は、
①問題文に『外接円の半径』が出てきたら
②向かい合う辺と角が条件に与えられたら
余弦定理ってナニ?
続いては、余弦定理です。cosθ を用いた公式になります。
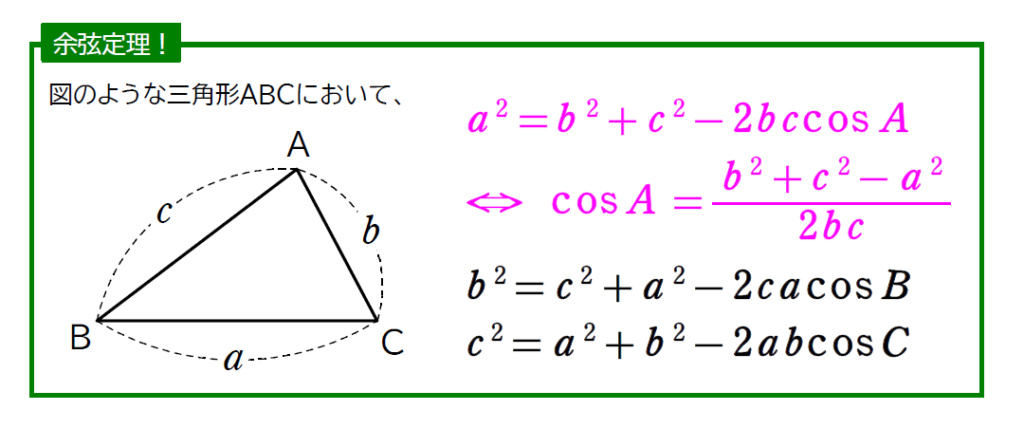
一番上の公式だけ下で証明しておきます。あとの公式は、変形するだけだったり、同じように証明できるものばかりですね。
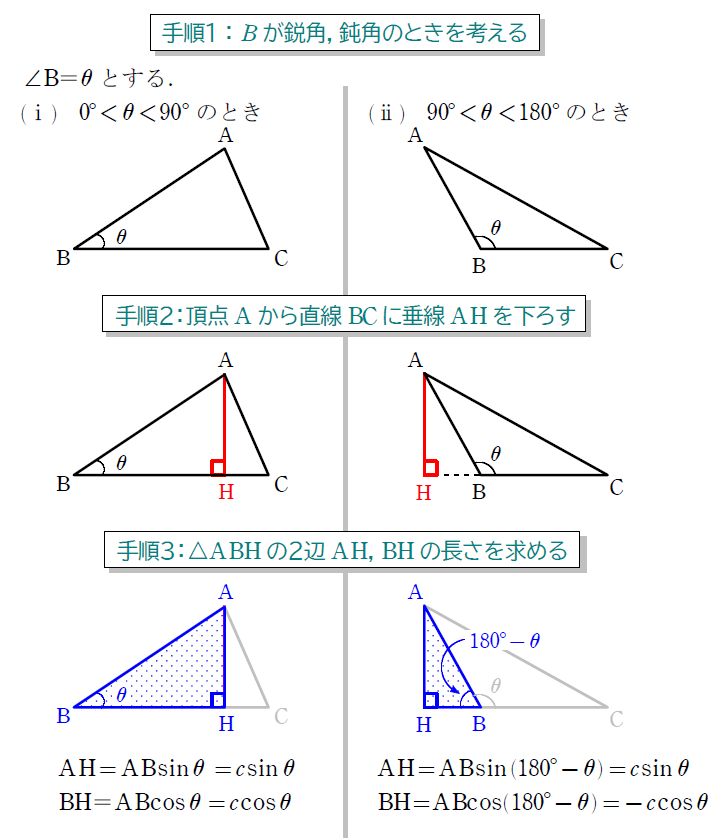
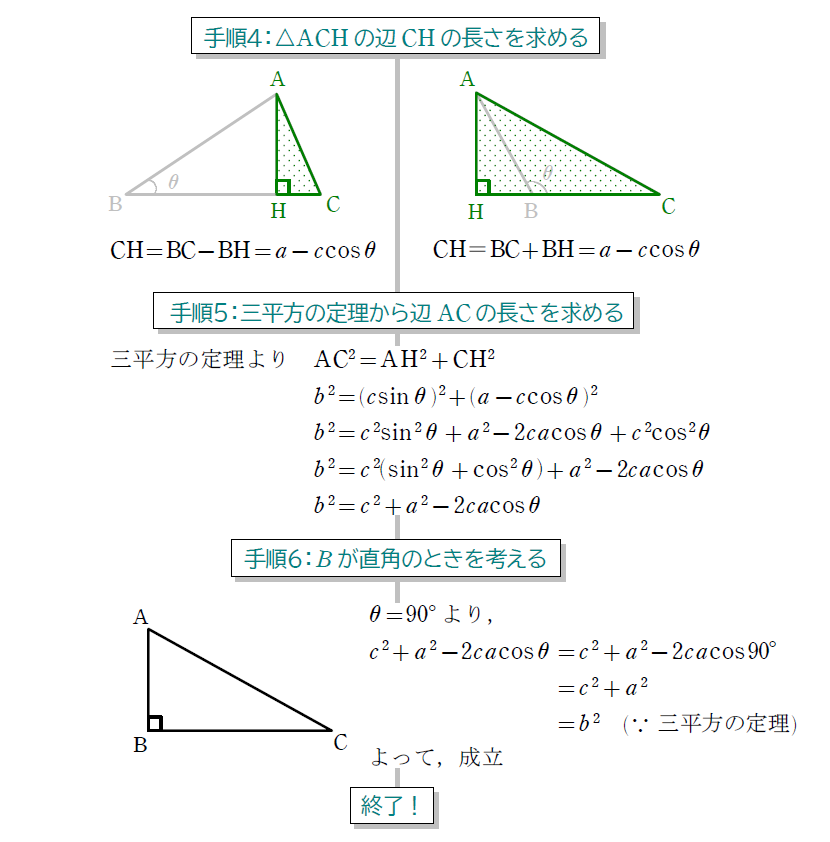
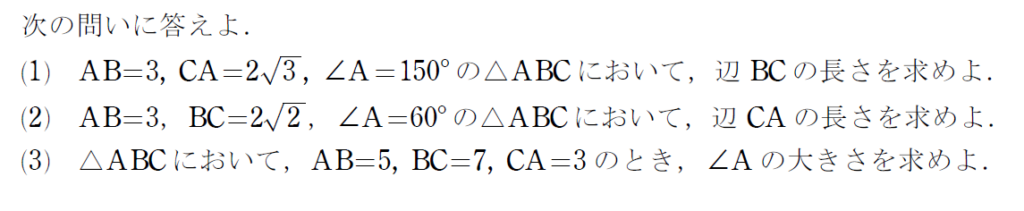
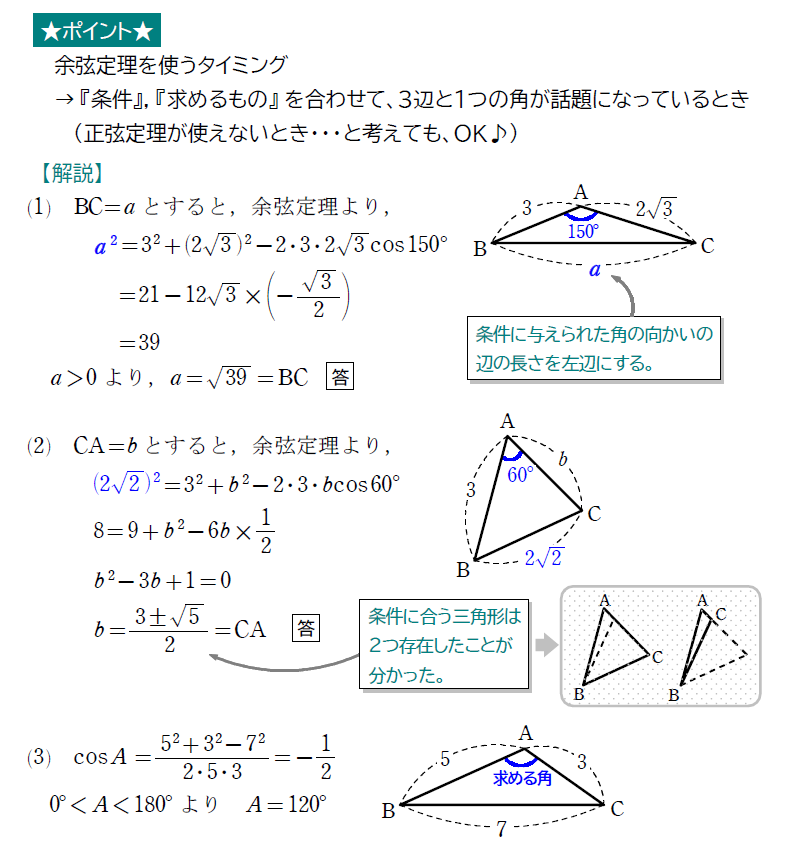

正弦定理と余弦定理の使い分けは、
『外接円の半径』『向かい合う辺と角が条件』→ 正弦定理
『条件,求めるもの合わせて3辺と1角』→ 余弦定理
という説明になりますが、「そんなこと覚えてられない」ってのが本音です。
現実的には、『正弦定理 → 余弦定理』の順で使えるかどうかを疑っていけば良いと思います。
三角形の面積
さて、続いては、三角形の面積の求め方を紹介します。
あれ?『底辺×高さ÷2』で出せるじゃんって思いましたよね?
三角形の面積ってイマサラ?
今回は高さが分かっていない三角形の面積がパパッと出せてしまう公式です!
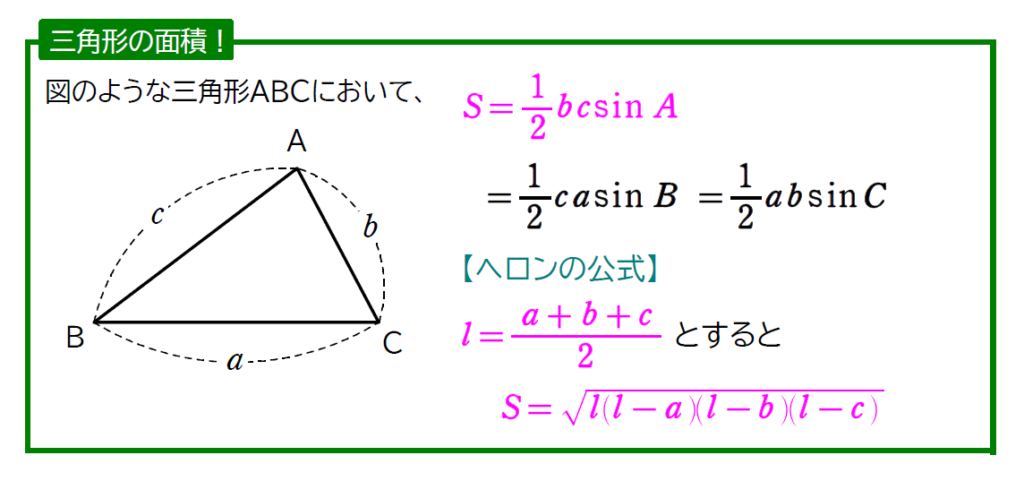
証明は余弦定理のときと同じような感じでいけるので、今回は省略します。
ただ、ヘロンの公式 は同じように・・・とはいかないので、下で証明しておきます。
下の証明は例題3を見てからの方が理解しやすいと思います。後から確認しましょう!

実際の問題を見てみましょう!!

(1)は公式一発ですが、(2)は角度が分かっていないですね? どうしましょ・・・

(2)はヘロンの公式で解いた方が圧倒的に楽でしたよね。
「じゃあ、別解だけで良くない?」な~んて声が聞こえてきそうですが、ヘロンの公式も万能ではないんです。
3辺の長さが有理数のときは上の解答と同じように簡単に解けますが、3辺の長さに無理数が含まれていたら、どうでしょう?
面倒な2重根号が生まれて、「もう無理!!!」ってことになります。無理数が含まれているときは、余弦定理を利用して、cosθ → sinθ を求めましょう!
まとめ and 確認テスト!
どうでしたか?三角比の利用方法は分かってきたでしょうか?
正弦定理、余弦定理、三角形の面積の公式は、三角形の内接円の半径や円に内接する四角形の問題など、三角比の応用問題を解く上で必須の公式となります。
また、これから他の色々な単元でお世話になるので、しっかりと練習しておきましょう。
三角比の値や相互関係に不安がある人は『前回の記事』を参考にしてください。
確認テストはこちらから!
続きや前の内容はこちらから!
他の単元の学習はこちらから!






コメント