こんにちは。ねこの数式のnanakoです。
三角比の値,相互関係,正弦定理,余弦定理,三角形の面積、基本的な公式などの確認は済みましたか?
これらのものに加え、角の2等分線の特徴,内接四角形の特徴,内接円の半径の公式,トレミーの定理,方べきの定理を使った応用問題の紹介をしていきたいと思います。今回、紹介するような問題をできるようにしていけば、三角比はバッチリです。
定期テスト、大学入試に向けて、しっかりと仕上げていきましょう。
三角比の値の覚え方に不安がある人は下の記事の埋め込み動画を確認してください。
三角比の方程式・不等式など!
まずは、三角比を用いた問題の数式編を紹介します。
相互関係の応用問題ってナニ?
相互関係がメインとなる問題を見てみましょう。

見た目はエグイですが、工夫の仕方が分かると簡単です。

数学では値の代入をギリギリまで待った方が楽に解ける問題が多いです。今回のように代入される側の式を変形し、キレイにしてから代入するクセをつけておきましょう。
続いては、『三角比+対称式』の応用問題です。
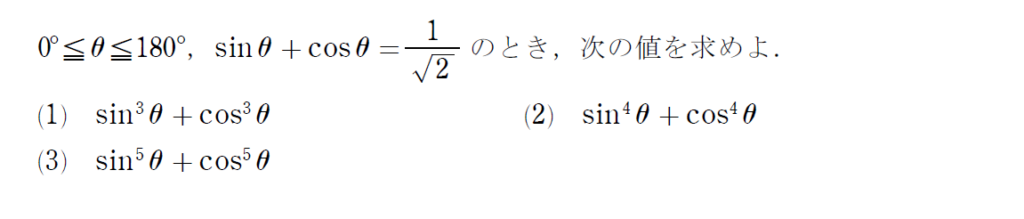
(1)は基本問題です。忘れてしまっている場合は下の記事を参考にしてください。


3乗、4乗、5乗の解き方を確認しましたが、6乗が出てきた場合はどうすれば良いか分かりますか?
答えは、\(\small \sin^3\theta+\cos^3\theta \) の2乗の利用です!
三角比の方程式・不等式ってナニ?
『方程式・不等式を解く』とは、代入して成立する値や範囲を求めることをいいます。

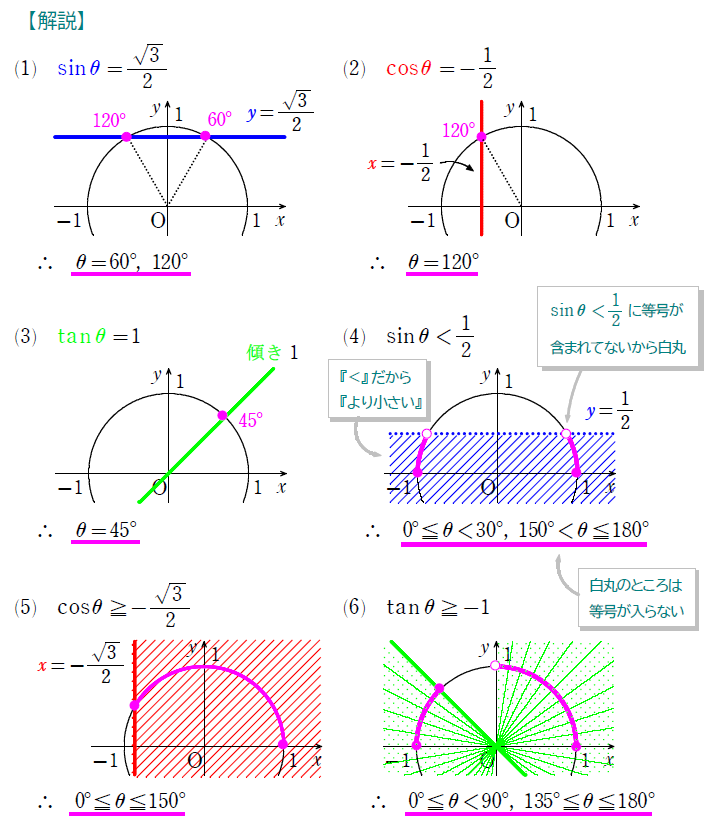
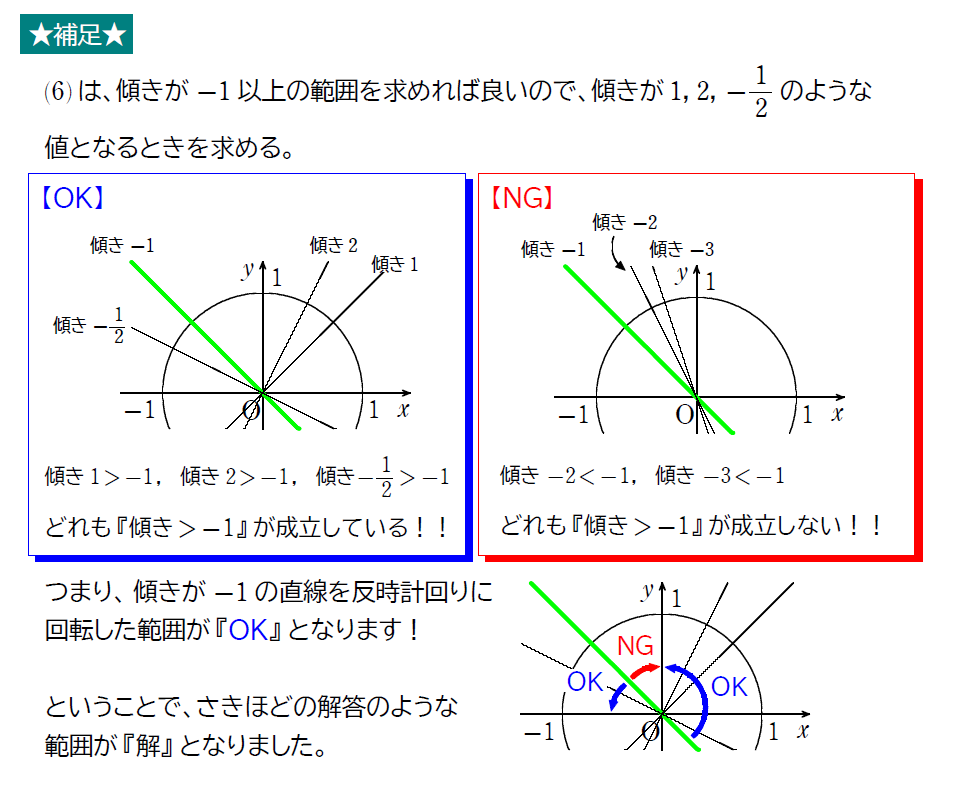
どうでした?難しかったですか?
実は、上の例題は応用問題ではなく、ただの準備運動です。(がーん)
次が本題の応用問題となります!


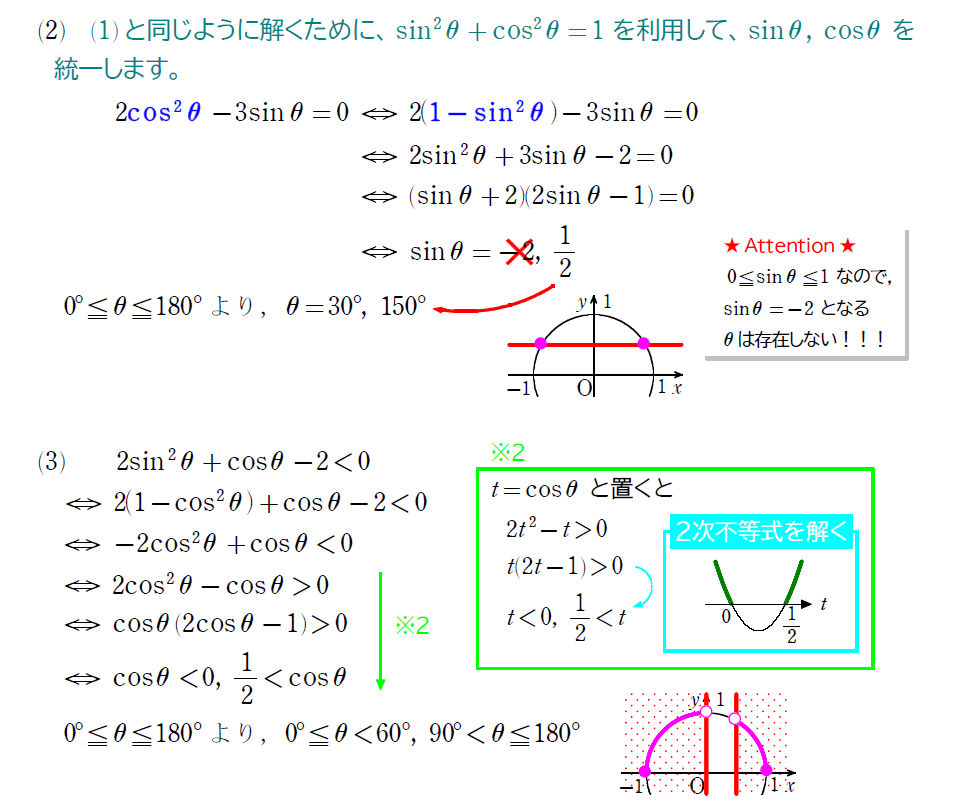
今後の数学の問題では、上のように2次方程式・2次不等式と融合するのはよくあることです。この問題で慣れておきましょう。
2次不等式の解法が怪しい人は、下の記事を参考にしてください。
三角形や四角形の問題!
さて、メインディッシュである図形問題の応用編です!
実際の入試問題でもよく出題される問題ばかりなので、しっかり学習しておきましょう。
内接円の半径ってナニ?

上の公式は、面積 S= となっていますが、面積を求めるのに使うことはほぼ無いです。内接円の半径を求めるために使う公式だと思ってよいです。
この公式は仕組みを理解しながら利用した方が、公式も覚えやすいですし、今後似たような公式が出てくるのでお得です。
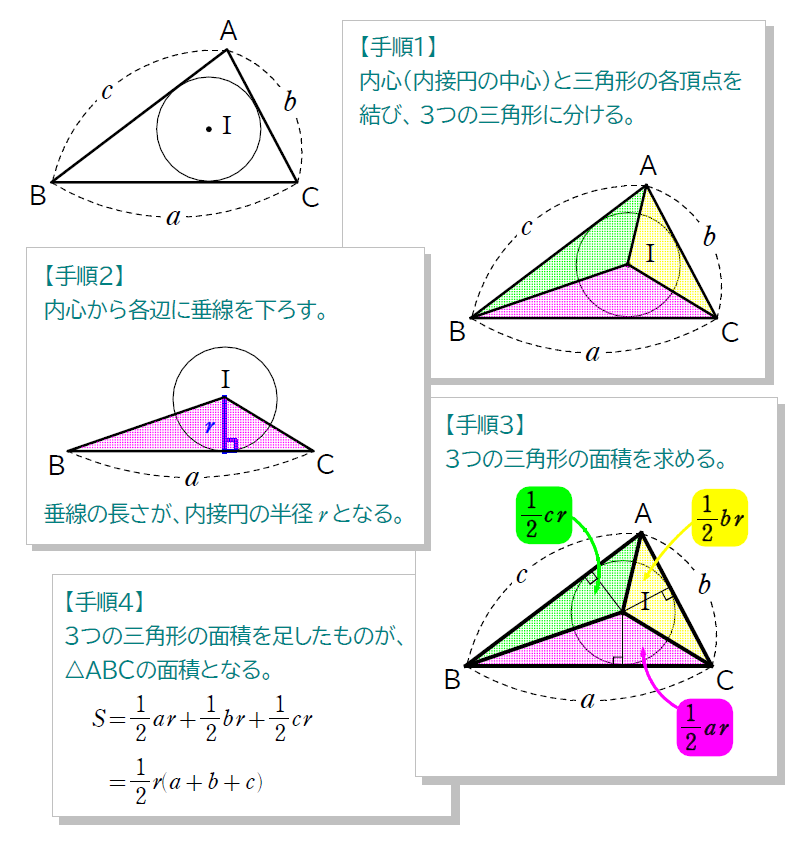
内接円の半径にまつわる問題は、上の公式を知っていれば秒殺です。

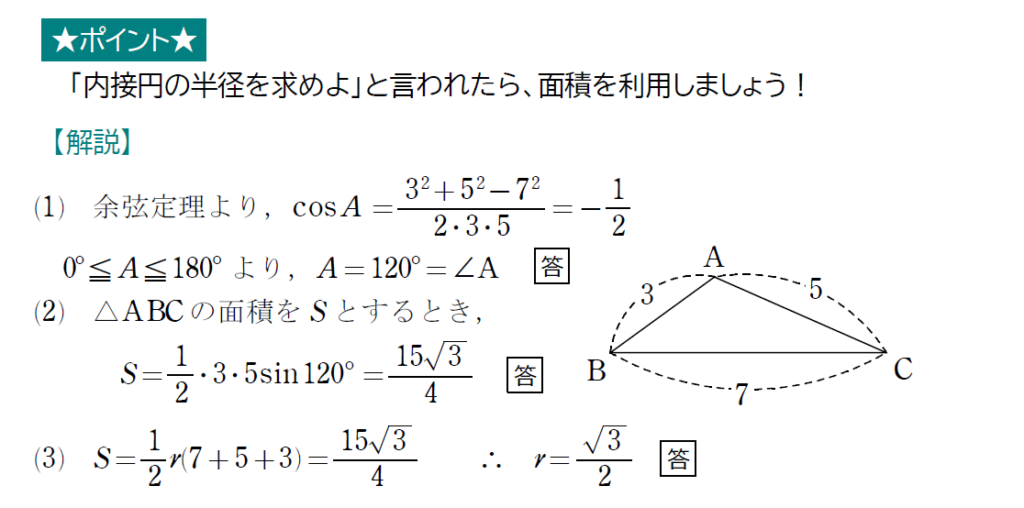
外接円の半径を求める問題とごっちゃにならないように気をつけてください。
内接円の半径 → 面積を利用
外接円の半径 → 正弦定理を利用
セットで確認しておきましょう。
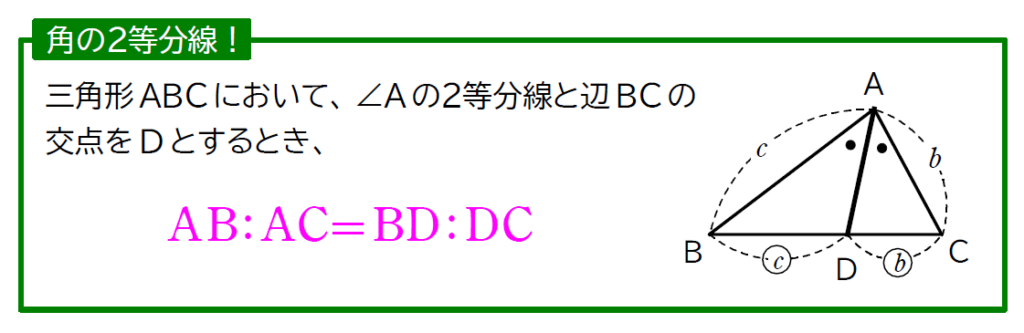
角の2等分線ってナニ?
角の2等分線というのは、角度を半分にする直線のことを指します。角の2等分線の問題の中でも、まずは簡単な問題を紹介したいと思います。


上の解法が使えるのは、2等分される角が 60°, 90°, 120° のときだけです。それ以外の角度のときに利用すると、有名角ではなくなってしまうため、サインの値が出せなくなってしまいます。
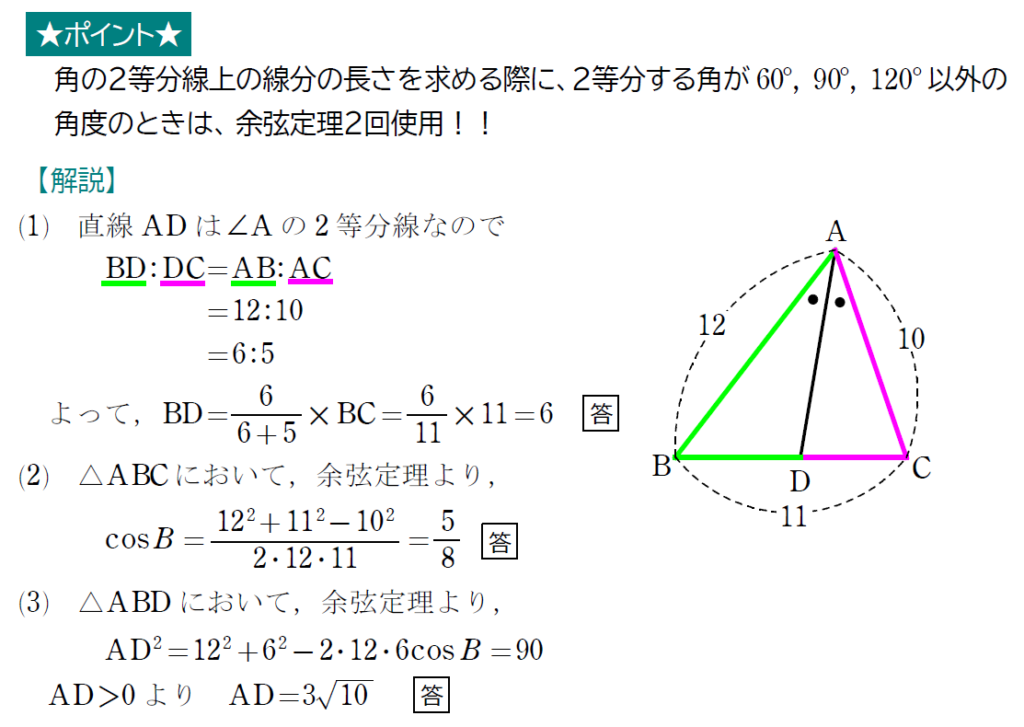
続いての問題は、面積が利用できないような問題です。

さて、本題の線分ADの求め方を確認する前に、(1)の線分BDを出すための公式を確認していきましょう。
この公式は、三角比以外でもお世話になる公式なので、よく覚えておきましょう。
内接四角形ってナニ?
円に内接する四角形、通称、内接四角形の問題を見ていきましょう。
そのためにも、まずは内接四角形の特徴を見ていきたいと思います。


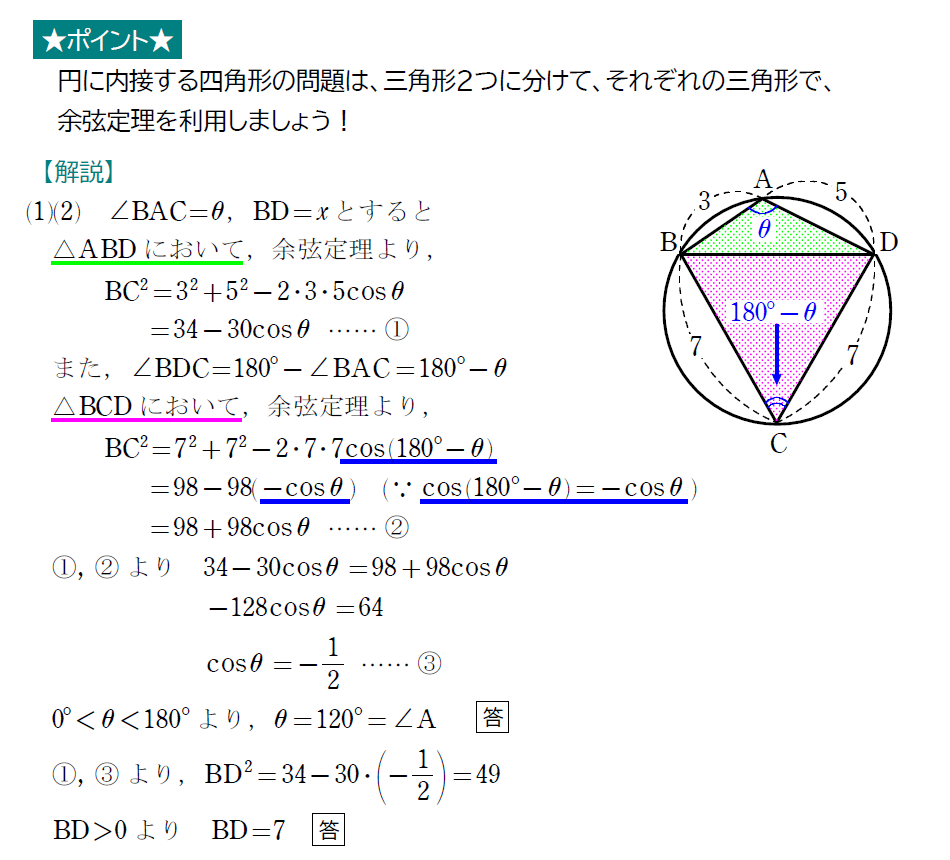

さて、例題8の解説は以上ですが、この問題は掘り下げると色々と出てくる問題です。余裕がある人は、下の内容も確認していきましょう!
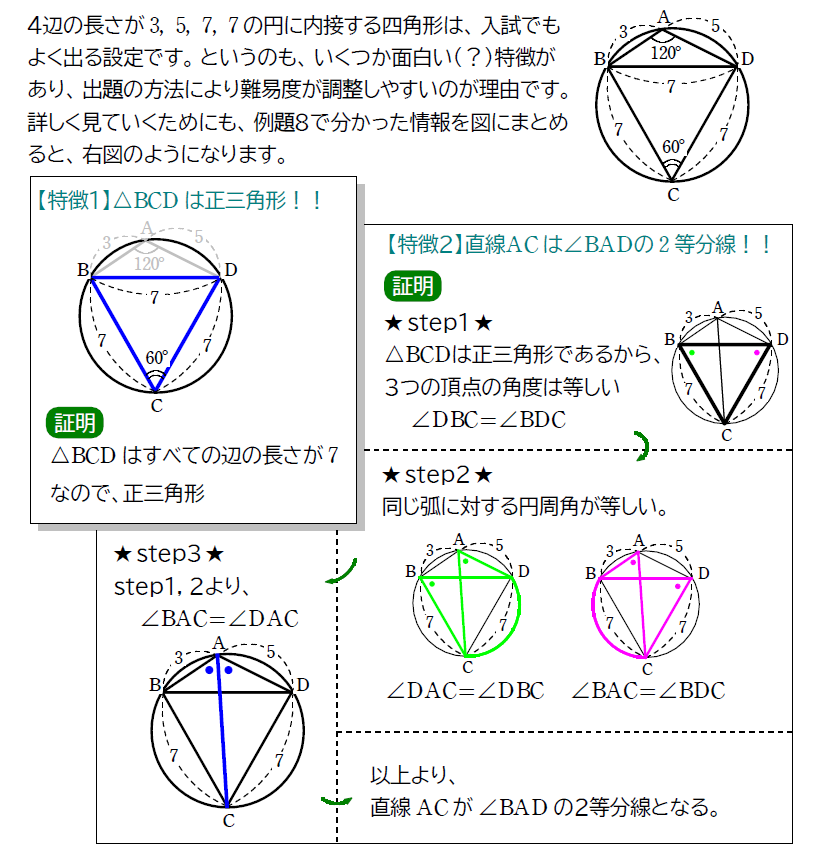
また、内接四角形の問題の中でも、さらに難しい問題を解く上では、他にも知っておかないといけない知識がいくつかあります。

四角形の面積の公式は、四角形の面積を求めるために利用することは少ないです。むしろ面積を他の方法で求めたうえで、対角線のなす角を求めることの方が多いと思います。

これは公式として使うのは賛否両論だと思います。というのも、教科書に公式として載っているものではないからです。入試においては利用しても問題ないと思いますが、定期テストで利用する場合は事前に学校の先生に聞いておいた方が無難化もしれません。
さて、これらの知識を利用した応用問題を紹介したいと思います。ここまでの内容に不安がある人は、しっかりと復習してからみてください。



さて、どうでしたか?もうひと頑張りしましょう!
(5)の解答は別解があります。
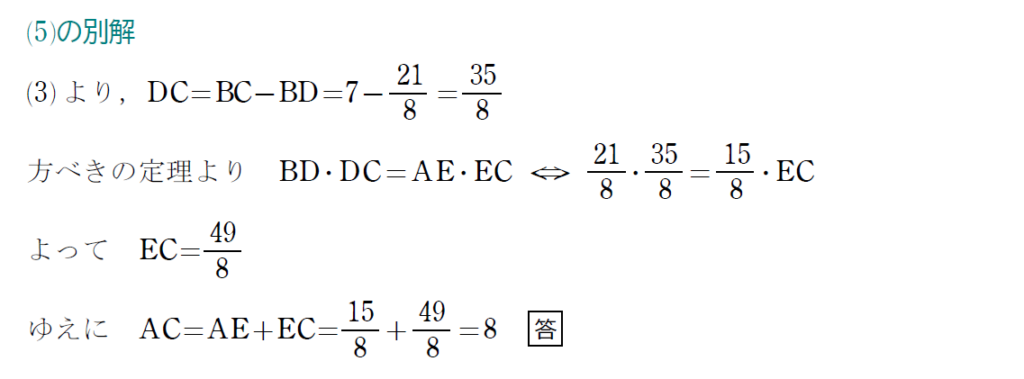
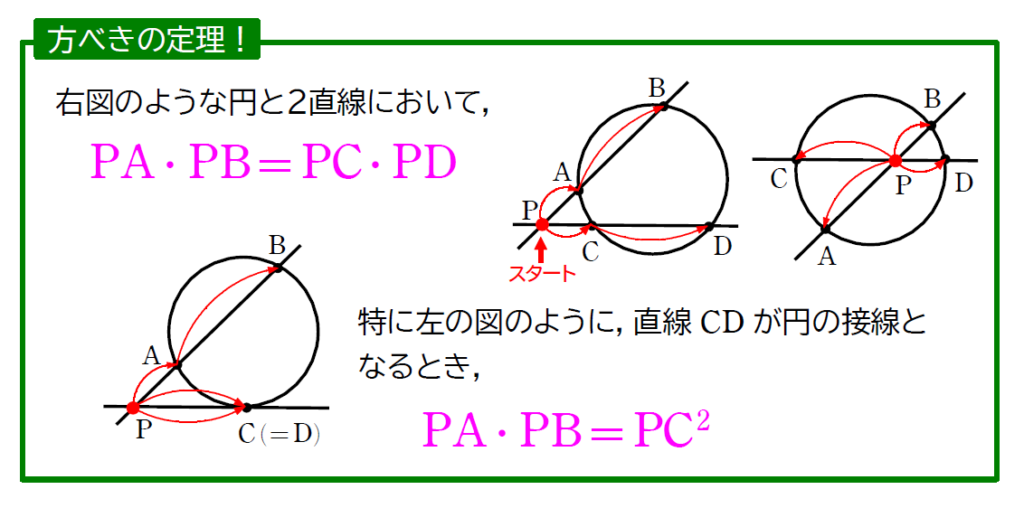
方べきの定理はしっていましたか?下で紹介するので、覚えておきましょう。
内接四角形の問題と相性が良いのが、下の方べきの定理です。共通テストでもおなじみの公式で、応用問題だけではなく、基本問題でもよく使うので覚えておきましょう。
まとめ!
三角比の応用問題はいかがでしたか?
図形の応用問題は設定を変えることで、さらに難易度をあげることもできます。それらの問題に対応するためにも、今回紹介した
①内接円の半径を求める問題
②角の2等分線
③内接四角形
はしっかりと練習して身につけておきましょう。
確認テストはこちらから!
前の内容はこちらから!
数Ⅰはこれでおしまいです。
お疲れさまでした。
他の単元の学習はこちらから!







コメント