こんにちは。ねこの数式のnanakoです。
今回は、因数分解の中でも重要な「たすき掛け」や「置き換えを利用した因数分解」を中心に見ていきます。
特に「たすきが掛け」は因数分解の方法の中でも主役となるものです。
基本的な問題はもちろん、文字がたくさん入った複雑な問題も見ていくので、頑張りましょう。
たすき掛け
たすき掛け?
念のため中学校の因数分解を確認しましょう。
\(\small(1) x^2+(a+b)x+ab=(x+a)(x+b)\)
\(\small(2) x^2+2xy+y^2=(x+y)^2\)
\(\small(3) x^2-y^2=(x+y)(x-y)\)
例.\(\small x^2+5x+6=(x+2)(x+3)\)
かけて \(\small 6\)、足して \(\small 5\) となる組が \(\small 2\) と \(\small 3\) だから上のように因数分解されました。
では、さっそく高校で最もよく使う『たすきがけ』をみていきましょう。
\(\small acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
いや~、さっぱり分からないですよね。
公式を覚えて利用するというのは現実的ではないので、表を利用した『たすきがけ』というものを見ていきたいと思います。
そのためにも、まずは展開を参考に考えていきましょう。
図1のような分配を図2のように縦に並べてみます。さらに係数だけをメモしたのが図3となります。
図3のような表をたすきがけと言って、この表が出来れば逆の流れで因数分解が出来ます。 具体的な問題で見ていきましょう。
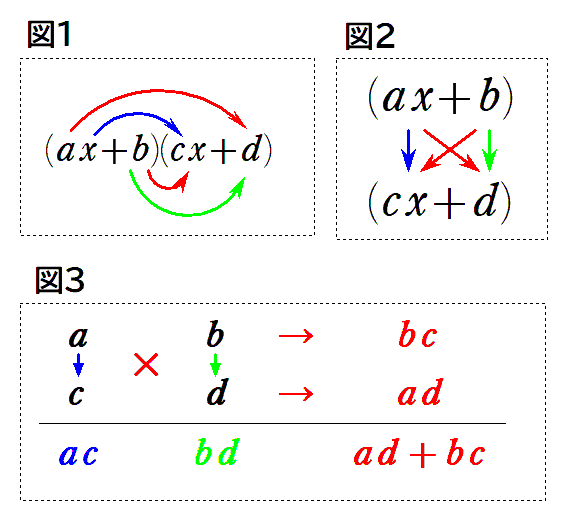
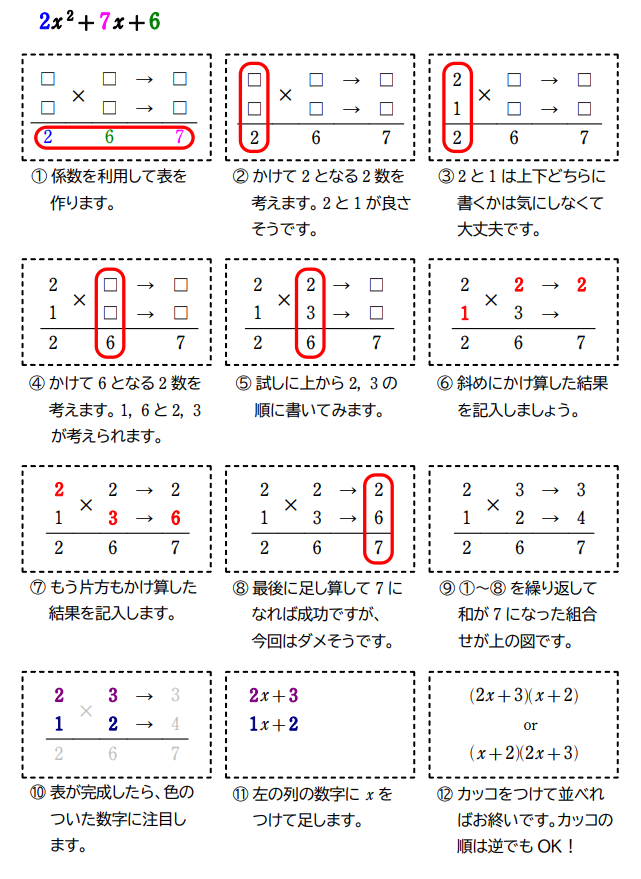
次の式を因数分解せよ。
\(\small(1) 2x^2+7x+6\\[4pt]
\small(2) 6x^2+11x+3\\[4pt]
\small(3) 3x^2-2x-5\\[4pt]
\small(4) 4x^2-8xy+3y^2\\[2pt]
\displaystyle\small(5) 2x^2+6x+ \frac{5}{2}\)
\(\small(1)\) 下の ① ~ ⑫ の作業でたすきがけを行っていきましょう。

「たすきがけ」はいかがでしたか?
たくさん量をこなして、素早く因数分解できるようにしていきましょう。
係数に文字を含んだたすき掛け
さて、続いては「係数に文字を含んだたすきがけ」です。
係数とはある文字にかかっている数式 (数または式) を指します。
例.\(\small 5x^2+2xy+y^2\) について
① \(\small x^2\) の係数は \(\small 5\)
② \(\small x\) の係数は \(\small 2y\)
「係数に文字を含んだたすきがけ」は文字がたくさん出てくる因数分解です。とにかく難しそうに見えます。
ですが、数式の見方を変えてあげると、だいぶ簡単に見えてきます。実際の問題で見てみましょう。
次の式を因数分解せよ
\(\small(1) ax^2+(a^2+3)x+3a\)
\(\small(2) ax^2+b(a+2)x+2b^2\)
\(\small(3) 2x^2-(3a-1)x+a^2-1\)
数学の問題を解く上で、重要な考え方として、「文字が複数あるときは1文字に注目」というものがあります。注目しなかった文字は定数(数字)扱いしましょう。

慣れないと難しい計算ですよね。
高校では文字の種類がたくさん出てくる問題が頻繁に出てくるようになります。
その際にこの「1文字に注目する計算方法」で乗り切ることになるので、この問題を通してしっかりと練習しておきましょう。
公式や置き換えを利用した因数分解
3次式の因数分解
今回は公式に当てはめて因数分解する問題です。
使うのは、『展開・因数分解①』の例題1で確認した展開公式の逆です。
\(\small(1) x^3+3x^2y+3xy^2+y^3=(x+y)^3\)
\(\small(2) x^3-3x^2y+3xy^2-y^3=(x-y)^3\)
\(\small(3) x^3+y^3=(x+y)(x^2-xy+y^2)\)
\(\small(4) x^3-y^3=(x-y)(x^2+xy+y^2)\)
展開のときと同じで、\(\small (2)\) は覚えずに \(\small (1)\) を流用します。また 【公式】の (3) と (4) は高校では、とにかくよく使う公式なのですぐに覚えましょう!
次の式を因数分解せよ。
\(\small(1) x^3-6x^2+12x-8\)
\(\small(2) x^3+8\)
\(\small(3) 27x^3-8y^3\)
\(\small\begin{eqnarray}
(1)& &x^3-6x^2+12x-8\\
&=&x^3+3\cdot x^2\cdot (-2)^1+3\cdot x^1\cdot (-2)^2+(-2)^3\\
&=&(x-2)^3\\
\end{eqnarray}\)
\(\small \begin{eqnarray}
(2)& &x^3+8\\
&=&x^3+2^3\\
&=&(x+2)(x^2-x\cdot 2+2^2)\\
&=&(x+2)(x^2-2x+4)
\end{eqnarray}\)
\(\small \begin{eqnarray}
(3)& &27x^3-8y^3\\
&=&(3x)^3-(2y)^3\\
&=&(3x-2y)\{(3x)^2+(3x)\cdot(2y)+(2y)^2)\}\\
&=&(3x-2y)(9x^2+6xy+4y^2)
\end{eqnarray}\)
\(\small (1)\) の解説は正しい説明ではあるのですが、ホンネを言うとめんどくさい方法だと思います(笑)
実際の流れとしては、\(\small \color{red}{x^3}-6x^2+12x-\color{blue}{8}\) の \(\small \color{red}{x^3} \) と \(\small \color{blue}{8}\) の部分が、\(\small \color{red}{(x)^3}\) と \(\small \color{blue}{2^3}\) と表せるので、\(\small (\color{red}{x}-\color{blue}{2})^3\) と推測してしまいます。
あとは展開して元に戻るか確認すればOKです。
置き換えを利用した因数分解
次は、公式を利用して因数分解するのではなく、展開の工夫を利用した問題を見ていきましょう。
次の式を因数分解せよ。
\(\small(1) (x+1)(x+2)(x+3)(x+4)-15\)
\(\small(2) x(x+1)(x+2)(x+3)-24\)
\(\small (x+1)(x+2)(x+3)(x+4)\) の展開の仕方は、『展開・因数分解①』にある例題2を確認しましょう。
\(\small\begin{eqnarray}
(1)& &(x+1)(x+2)(x+3)(x+4)-15\\
\small&=&(x^2+5x+4)(x^2+5x+6)-15\\
\small&=&(A+4)(A+6)-15 (A=x^2+5x)\\
\small&=&A^2+10A+9\\
\small&=&(A+1)(A+9)\\
\small&=&(x^2+5x+1)(x^2+5x+9)\\
\end{eqnarray}\)
\(\small\begin{eqnarray}
(2)& &x(x+1)(x+2)(x+3)-24\\
\small&=&(x^2+3x)(x^2+3x+2)-24\\
\small&=&A(A+2)-24\\
\small&=&A^2+2A-24\\
\small&=&(A-4)(A+6)\\
\small&=&(x^2+3x-4)(x^2+3x+6)\\
\small&=&(x+4)(x-1)(x^2+3x+6)\
\end{eqnarray}\)
注意1:最初にくくれるものが無いか確認しましょう。
注意2:最後にカッコの中を因数分解できるかチェックしましょう。
まとめ and 確認テスト!
ここまでが因数分解の基本です。この記事で出てきた内容は、どれもこれも重要なものばかりです。
例題2は基本と呼ぶには難しいと感じますが、続きの因数分解の話を踏まえると、ここまででしっかりと出来るようにしておきたいです。
頑張りましょう!
確認テストはこちらから!
続きや前の内容はこちらから!






コメント