分かりやすい【１次不等式】不等式の特性を徹底解剖！

こんにちは。ねこの数式のnanakoです。

突然ですが、 $\small 4$ と $\small 6$ はどちらが大きい数でしょうか？もちろん、 $\small 6$ の方が大きい数ですね (笑)

このような数の大小関係を、数式でどのように表すかを見ていきましょう。

目次！

不等式の特性
- 不等号とは？
- 不等式の特性は？
１次不等式
- １次不等式の解き方
- 不等式と数直線
連立不等式
不等式の応用問題
- 方程式・不等式の解
- 不等式を満たす整数
まとめ

不等式の特性

不等号とは？

$\small 4$ と $\small 6$ の大小関係は、「 $\small \bf4<6$ 」と表します。「 $\small <$ 」を不等号と呼び、大きい数の方に開いた形で使います。

例． $\small -3<-2,　\sqrt{5}>2$

「 $\small \bf<$ 」は小なり、「 $\small \bf>$ 」は大なりと読みます。上の式のように不等号を用いた式のことを不等式と呼びます。

今回はこの不等式について見ていきましょう。

不等式の特性は？

不等式を計算していく上での特性についてみていきます。 $\small 4<6$ に対して、以下の計算をすると、不等号の向きがどうなるか見ていきましょう。

両辺に $\small 3$ を足したとき、 $\small 4+3=7$ と $\small 6+3=9$ を比較して、
　 $\small\bf 4+3<6+3$
両辺から $\small 3$ を引いたとき、 $\small 4-3=1$ と $\small 6-3=3$ を比較して、
　 $\small\bf 4-3<6-3$
両辺に $\small 2$ をかけたとき、 $\small 4\times2=8$ と $\small 6\times2=12$ を比較して、
　 $\small\bf 4\times2<6\times2$
両辺を $\small 2$ で割ったとき、 $\small 4\div2=2$ と $\small 6\div2=3$ を比較して、
　 $\small\bf 4\div2<6\div2$
、 $\small 4\times(-2)=-8$ と $\small 6\times(-2)=-12$ を比較して、
　 $\small\bf 4\times(-2)$ $\small\bf\color{red}{>}$ $\small\bf 6\times(-2)$
、 $\small 4\div(-2)=-2$ と $\small 6\div(-2)=-3$ を比較して、
　 $\small\bf 4\div(-2)$ $\small\bf\color{red}{>}$ $\small\bf 6\div(-2)$

両辺に負の数をかけたとき (⑤) と、両辺を負の数で割ったとき (⑥) だけ、不等号の向きが変化しましたね。これを文字で表したのが、下の公式です。

【公式】不等式の特性　

不等式 $\small a\color{blue}{<}b$ について
$\small(1)　a+c\color{blue}{<}b+c$
$\small(2)　a-c\color{blue}{<}b-c$
$\small(3)$ 　 $\small c>0$ のとき、 $\small ac\color{blue}{<}bc$
$\small(4)$ 　 $\small c>0$ のとき、 $\small \displaystyle\frac{a}{c}\color{blue}{<}\frac{b}{c}$
$\small(5)$ 　のとき、 $\small ac$ $\small\bf \color{red}{>}$ $\small bc$
$\small(6)$ 　のとき、 $\small \displaystyle\frac{a}{c}$ $\small\bf \color{red}{>}$ $\small\displaystyle\frac{b}{c}$ 　

今度は、次の $\small2$ 式を見てみましょう。

例． $\small(1)　x>1$
　　 $\small(2)　x≧1$ 　

$\small (1)$ の不等式は、 $\small x$ と $\small 1$ を比較すると、「 $\small x$ の方が大きい」という意味ですね。言い換えると「 $\small x$ は $\small 1$ より大きい」となります。

では、 $\small (2)$ の不等式はどうでしょうか？「 $\small >$ 」の下に「 $\small =$ 」があります。これは「大なりイコール」と読み、「 $\small >$ 」でも「 $\small =$ 」でも良いですよ～という意味です。つまり、 $\small x$ は $\small 1$ 以上ということとなります。

数式の見方を確認したところで、実際の問題の話に入っていきましょう。

１次不等式

次は１次不等式について見ていきます。１次不等式とは、不等式の中でも１次式 (1乗) しか含まれないもののことです。

１次不等式の解き方

そもそも、不等式を解くとはどういうことでしょうか？

「方程式・不等式を解く」というのは、代入して成立する $\small x$ を求めることをいいます。ちなみに、求めた $\small x$ は解といいます。

では、実際の問題を見てみます。

例題１

次の不等式を解け。
$\small(1)　3x+7>1$
$\small(2)　x+1≧5x+8$

解説

$\small(1)$ 　方程式のときと同じように計算していきます。
　① $\small 3x+7>1$ の両辺から $\small 7$ を引きます。
　　 $\small　3x+7-7>1-7$
　　 $\small　3x>-6$
　② 両辺を $\small 3$ で割ります。
　　 $\small　3x\div3>-6\div3$
　　 $\small　x>-2$

なな

①は方程式の移行と同じ計算ですね。

はち

②も方程式のときと同じような計算だ！

$\small(2)$ 　① 方程式のときと同じように移行します。
　　 $\small　x-5x≧8-1$
　　 $\small　-4x≧7$
　② 両辺を $\small -4$ で割ります。
　　 $\small　x\color{red}{≦}7\div(-4)$
　　 $\small　x≦\displaystyle-\frac{7}{4}$

はち

あれ？不等号の向きが変わったよ。

なな

両辺を負の数で割ったからですよ。

ちなみに、 $\small (1)$ の解は、代入して成立する $\small x$ は $\small -2$ より大きい数ということを示してますよ。

不等式での計算は、基本は方程式のときと同じです。両辺に負の数をかけたときと、両辺を負の数で割ったときだけ、不等号の向きが変わるので注意しましょう。

不等式と数直線

問題を解いていくうえで不等式を図示したくなる場面がでてきます。その際、好き勝手に図示していいのではなく、あるルールのもとに図示していきます。

今回は、不等式を数直線に表す方法を見ていきましょう。

数直線は右に行けば行くほど大きい数、左に行けば行くほど小さい数が並んでいます。例えば、 $\small x>3$ という式を数直線に表すときは、数直線の $\small 3$ よりも右側が含まれることが分かるように図示します。

また等号 (イコール) が含まれているかどうかで図示の仕方が変わります。
$\small (ⅰ)$ 等号が含まれないときは白抜きの〇を利用し、数直線に対し斜めに線を描きます。
$\small (ⅱ)$ 等号が含まれるときは黒塗りの●を利用し、数直線に対し垂直に線を描きます。

言葉で説明しても分かりづらいだけなので、以下の①～⑥を確認しましょう。

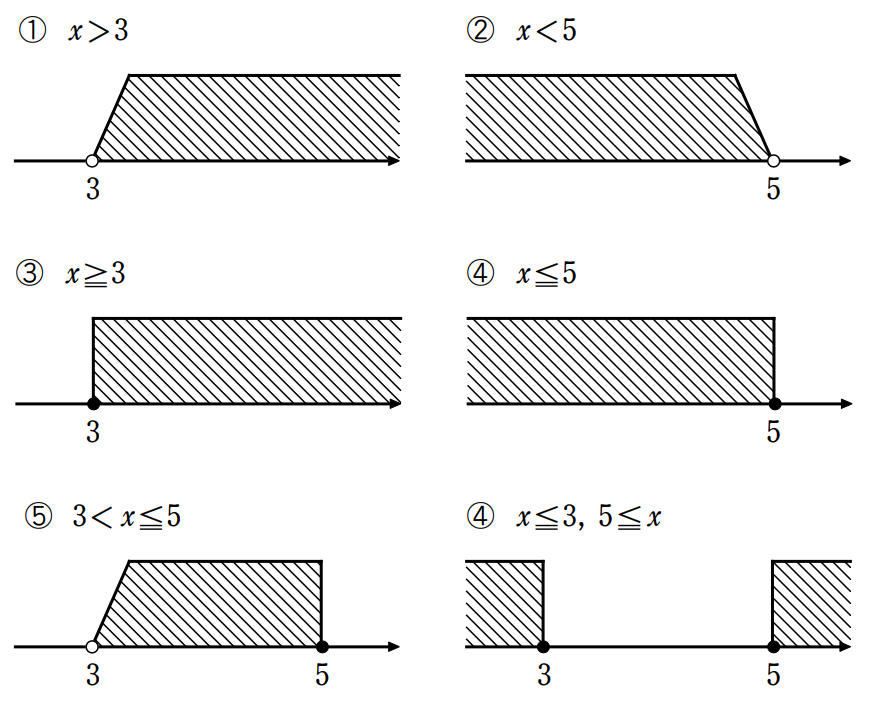
数直線に対して斜めか垂直かは、実際は守られていないこともあります。ただし、〇か●かは守るのが常識となっているので気を付けましょう。

連立不等式

まずはみなさんも知っている連立方程式の確認からしていきましょう。

例． $\small\begin{cases}\begin{eqnarray} 2x+y&=&5　&\cdots\cdots\cdots&\,①\\ x+y&=&3&\cdots\cdots\cdots&\,② \end{eqnarray}\end{cases}$ を解け。

連立方程式を解くというのは、①と②を同時に満たす $\small x$ と $\small y$ を求めることでした。

この問題では ① $\small -$ ② を計算すると、 $\small x=2$
これを①または②に代入して、 $\small y=1$ と求めました。

では、連立不等式を見ていきましょう。

例題２

次の連立不等式を解け。
$\small(1)　\begin{cases}3x+1<x+3\\2x-3≦5x+6\end{cases}$
$\small(2)　\begin{cases}2x-1≧5x+2\\4x-1<3x+2\end{cases}$

連立不等式も $\small 2$ 式を満たす $\small x$ を求めることとなります。ただ、連立方程式と違い、 $\small 2$ 式を組み合わせて解くわけではないです。連立不等式はそれぞれ別々に解いたうえで、最後に $\small 2$ 式を満たす $\small x$ の範囲を求めます。

解説

$\small(1)　\begin{cases} 3x+1<x+3　\cdots\cdots\cdots\,①\\ 2x-3≦5x+6\,\cdots\cdots\cdots\,②\end{cases}$
　①より、 $\small 2x<2$
　　　　　 $\small x<1$
　②より、 $\small -3x≦9$
　　　　　 $\small x≧-3$
　①, ②を同時に満たす $\small x$ の範囲は、 $\small -3≦x<1$

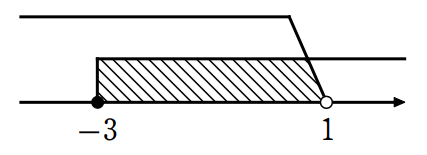
$\small(2)　\begin{cases} 2x-1≧5x+2　\cdots\cdots\cdots\,①\\ 4x-1<3x+2\,\,\,\cdots\cdots\cdots\,②\end{cases}$
　①より、 $\small -3x≧3$
　　　　　 $\small x≦-1$
　②より、 $\small x<3$
　①, ②を同時に満たす $\small x$ の範囲は、 $\small x≦-1$

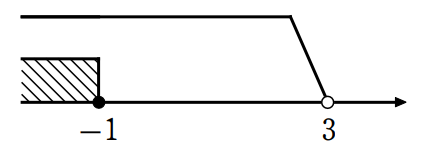
不等式の応用問題

ここまでの話をふまえて応用的な問題を見ていきましょう。どの問題も丸暗記は厳しいので、しっかりと理解していきましょう。がんばりましょう！

方程式・不等式の解

不等式の応用問題を見る前に、方程式の応用問題を見ていきます。

例題３

次の方程式を解け。
$\small (1)　(a+1)x-2a=2$
$\small (2)　ax=1$

下のポイントをあらためて確認してから、解説を見ていきましょう。

「方程式・不等式を解く」というのは、代入して成立する $\small x$ を求めることをいいます。ちなみに、求めた $\small x$ は解といいます。

解説

$\small(1)　(a+1)x=2(a+1)$
　 $\small(ⅰ)　a+1=0$ 　つまり　 $\small a=-1$ のとき
　　 $\small 0\cdot x=0$ となるので、解は　すべての実数
　 $\small(ⅱ)　a+1≠0$ 　つまり　 $\small a≠-1$ のとき
　　両辺を $\small a+1$ で割ると
　　 $\small x=2$ となり、解は　 $\small x=2$
　 $\small (ⅰ)(ⅱ)$ より、解は
　　 $\small a=-1$ のとき、すべての実数
　　 $\small a≠-1$ のとき、 $\small x=2$

$\small (2)　ax=1$
　 $\small(ⅰ)　a=0$ のとき
　　 $\small 0\cdot x=1$ となるので、解なし
　 $\small(ⅱ)　a≠0$ のとき
　　 $\small x=\displaystyle\frac{1}{a}$ となるので、解は　 $\small x=\displaystyle\frac{1}{a}$
　 $\small (ⅰ)(ⅱ)$ より、解は
　　 $\small a=0$ のとき、解なし
　　 $\small a≠0$ のとき、 $\small x=\displaystyle\frac{1}{a}$

$\small(1)$ は、両辺を $\small a+1$ で割りたいのですが、 $\small a+1=0$ のときは、 $\small 0$ で割ることになります。数学の世界では、 $\small 0$ で割ることはできないので、 $\small 0$ のときと、そうじゃないときで場合分けが必要です。
$\small 0\cdot x=0$ となったとき、どんな数を $\small x$ に代入しても、成立します。このように、どんな数でも成立するときは、すべての実数と答えます。実数とは、整数や無理数など皆さんが知っている数を全部合わせたものと考えましょう。
$\small 0\cdot x=(0$ $\small)$ となったとき、どんな数を $\small x$ に代入しても、成立しません。このように、代入できる数が無いとき、解なしと答えます。

一般化して (文字で表して) みましょう。

方程式 $\small ax=b$ の解は
$\small(ⅰ)　a=0$ のとき
$\small　(ア)　b=0$ のとき、 $\small 0\cdot x=0$ となるので、解はすべての実数
$\small　(イ)　b≠0$ のとき、 $\small 0\cdot x=(0$ $\small)$ となるので、解なし
$\small(ⅱ)　a≠0$ のとき
　両辺を $\small a$ で割って　 $\small x=\displaystyle\frac{b}{a}$

これをまとめたのが下の公式ですが、丸暗記をするのではなく、ちゃんと理解して使いましょう。

【公式】１次方程式の解　

方程式 $\small ax=b$ の解は
$\small　a=0、b=0$ のとき、すべての実数
$\small　a=0、b≠0$ のとき、解なし
$\small　a≠0$ のとき、 $\small x=\displaystyle\frac{b}{a}$

さっそく、実際の問題を見ていきましょう。

例題4

次の $\small x$ についての方程式・不等式を解け。
$\small(1)　ax+3≧x+3a$
$\small(2)　(a-1)x+4<x+a^2$

解説

$\small(1)　ax-x≧3a-3$
　　 $\small(a-1)x≧3(a-1)$
　 $\small (ⅰ)　a-1=0$ 　つまり　 $\small a=1$ のとき
　　　 $\small 0\cdot x≧0$ となるので、解は　すべての実数
　 $\small (ⅱ)　a-1>0$ 　つまり　 $\small a>1$ のとき
　　　両辺を $\small a-1$ で割ると、 $\small x≧3$
　 $\small (ⅱ)　a-1<0$ 　つまり　 $\small a<1$ のとき
　　　両辺を $\small a-1$ で割ると、 $\small x≦3$
　 $\small (ⅰ)$ ~ $\small(ⅲ)$ より、解は
　　 $\small a=1$ のとき、すべての実数
　　 $\small a>1$ のとき、 $\small x≧3$
　　 $\small a<1$ のとき、 $\small x≦3$

$\small(1)　(a-1)x-x<a^2-4$
　　 $\small(a-2)x<(a+2)(a-2)$
　 $\small (ⅰ)　a-2=0$ 　つまり　 $\small a=2$ のとき
　　　 $\small 0\cdot x<0$ となるので、解なし
　 $\small (ⅱ)　a-2>0$ 　つまり　 $\small a>2$ のとき
　　　両辺を $\small a-2$ で割ると、 $\small x<a+2$
　 $\small (ⅱ)　a-2<0$ 　つまり　 $\small a<2$ のとき
　　　両辺を $\small a-2$ で割ると、 $\small x>a+2$
　 $\small (ⅰ)$ ~ $\small(ⅲ)$ より、解は
　　 $\small a=2$ のとき、解なし
　　 $\small a>2$ のとき、 $\small x<a+2$
　　 $\small a<2$ のとき、 $\small x>a+2$

$\small a-1=0$ か $\small a-1≠0$ かどうかで場合分けするのは、例題３と同じ理由です。 $\small a-1≠0$ のとき、 $\small a-1>0$ と $\small a-1<0$ で分けるのは、正の数で割るのと、負の数で割るのでは、不等号の向きを変えるか変えないかに違いがでてくるからです。

これらの問題は単品で出題されることもありますが、今後の数学の問題を解いていると、突然この問題につながることも多いです。しっかりと理解した上で、使いこなしましょう。

不等式を満たす整数

例題５

連立不等式 $\small \begin{cases} 3x+1>2x+a \\ x+7≧4x-5 \end{cases}$ を満たす整数 $\small x$ が $\small 5$ 個存在するような定数 $\small a$ の値の範囲を求めよ。

解説

$\small \begin{cases} 3x+1>2x+a\,\,\cdots\cdots\cdots\,① \\ x+7≧4x-5　\cdots\cdots\cdots\,②\end{cases}$
① より　 $\small x>a-1$
② より　 $\small -3x≧-12$
　　　　 $\small \,\,x≦4$
①と②を同時に満たす整数 $\small x$ が $\small 5$ 個存在するので、 $\small 0,\,1,\,2,\,3,\,4$ が含まれることとなる。よって、これらの整数が含まれる $\small a-1$ の範囲は、
　 $\small -1≦a-1<0$
よって、求める $\small a$ の範囲は、
　 $\small 0≦a<1$

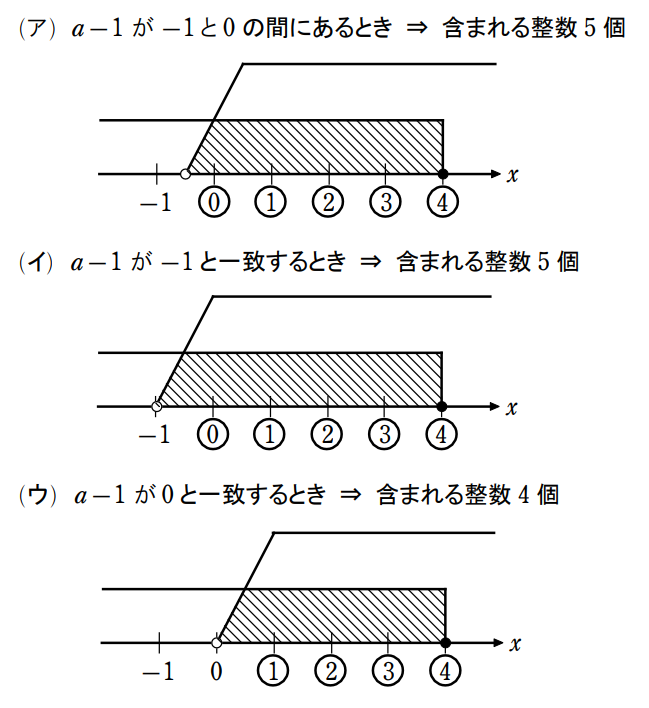
この問題は等号の入れ方がポイントです。ちゃんと理解をしていないと等号の入れ方が模範解答と逆になることが多いです。（例: $\small 0<a≦1$ ) これは $\small x$ の範囲と $\small a$ の範囲をごちゃ混ぜにしてしまっているからです。そうならないためには、実際に問題を解く際にも、めんどくさがらずに、右上図の (ア) ～ (ウ) を書いてみましょう。そうすれば、混乱しずらくなり、正しい等号の入れ方が見えてくると思います。

例題３は理解するのも大変かもしれませんが、それ以上に解いてみると間違えてしまう問題なので、しっかりと量をこなして、確実に解けるようにしていきましょう。