こんにちは。ねこの数式のnanakoです。
絶対値は、場合分けをして方程式や不等式を解いて・・・と、複雑な作業が多いので、高校で数学を習い始めて、最初に挫折する可能性が出てくる単元です。
ここを乗り切れると最初の定期試験で良い結果が見えてくるので、あきらめずに頑張りましょう!
絶対値と数直線
絶対値とは?
絶対値とは、数直線上で原点 \(\small 0\) からの距離を表す値です。
\(\small\color{magenta}{\vert \vert}\) のように\(\small 2\) 本の縦棒で挟んで表現します。
例.
\(\small ①\,\,\vert 3 \vert\,\,\cdots\) 数直線上で原点 \(\small 0\) から点 \(\small 3\) までの距離
\(\small ②\,\,\vert -3 \vert\,\,\cdots\) 数直線上で原点 \(\small 0\) から点 \(\small -3\) までの距離
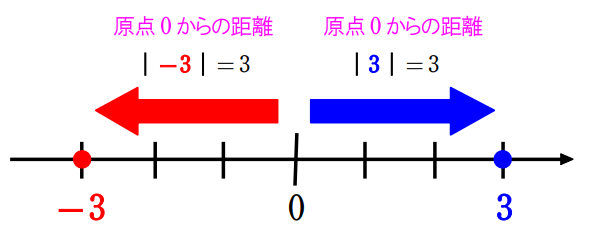
\(\small ①\) 数直線上で原点 \(\small 0\) から点 \(\small \color{blue}{3}\) までの距離は \(\small 3\) なので、\(\small\vert \color{blue}{3} \vert=3\)
\(\small ②\) 数直線上で原点 \(\small 0\) から点 \(\small -3\) までの距離は \(\small 3\) なので、\(\small\vert \color{red}{-3} \vert=3\)
\(\small\vert\) 〇 \(\small \vert\) を求めてみましょう。\(\small\vert\) 〇 \(\small \vert\) は原点 \(\small 0\) から点 〇 までの距離でしたね。
\(\small ①\)のように 〇 が正の数のときは、〇 がそのまま距離を表します。
\(\small ②\)のように 〇 が負の数のときは、符号を変えるために 〇 に \(\small \bf(-1)\) をかけると距離を表します。
では、これを公式にしたものを確認しましょう。
\(\small\vert x \vert=
\begin{cases}x\,\,&(x≧0)\\-x&(x<0)\end{cases}\)
公式の意味を詳しく説明していきます。\(\small\vert x \vert\) は数直線上で原点 \(\small 0\) から点 \(\small x\) までの距離を表します。
絶対値の中身の符号で外し方が変わることを押さえておきましょう。
次の値を求めよ。
\(\small(1) \left\vert \displaystyle\frac{1}{2} \right\vert\) \(\small \,(2) \vert -\sqrt{3} \vert\)
\(\small(3) \vert 2-\sqrt{5} \vert\) \(\small(4) \vert \pi-3 \vert\)
\(\small(1)\) \(\small \displaystyle \frac{1}{2}>0\) なので、\(\small\displaystyle\left\vert \frac{1}{2} \right\vert=\frac{1}{2}\)
\(\small(2)\) \(\small -\sqrt{3}<0\) なので、\(\small \vert -\sqrt{3} \vert=-\sqrt{3}\times(-1)=\sqrt{3}\)
\(\small(3)\) \(\small \sqrt{4}<\sqrt{5}\) なので、\(\small 2<\sqrt{5}\) である。
よって、\(\small 2-\sqrt{5}<0\) なので、\(\small \vert 2-\sqrt{5} \vert=(2-\sqrt{5})\times(-1)=\sqrt{5}-2\)
\(\small (4)\) \(\small \pi>3\) なので、\(\small \vert \pi-3 \vert=\pi-3\)
数直線を利用して解く方程式・不等式の問題
続いて絶対値が含まれる方程式と不等式の問題を見ていきます。
絶対値が含まれた方程式と不等式の問題は、「数直線を利用して解く」ものと「場合分けを利用して解く」ものがあります。
まずは、「数直線を利用して解く」ものを見ていきましょう。
まずは、方程式の問題です。
次の方程式を解け。
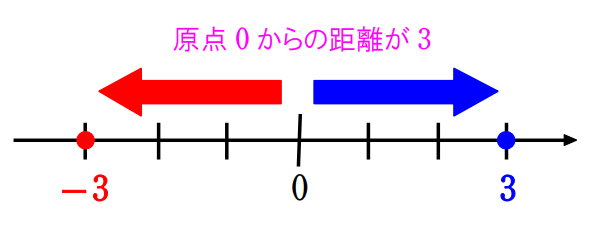
\(\small(1) \vert x\vert=3\)
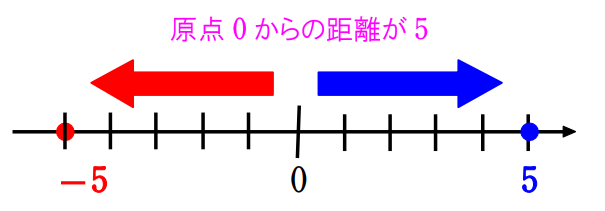
\(\small(2) \vert 2x-1\vert=5\)
\(\small(1)\) 原点 \(\small 0\) から点 \(\small x\) までの距離が \(\small 3\)、
つまり、点 \(\small x\) は原点 \(\small 0\) からの距離が \(\small 3\) の点です。
よって、\(\small x=\pm3\)
\(\small(2)\) 原点 \(\small 0\) から点 \(\small 2x-1\) までの距離が \(\small 5\)、
つまり、点 \(\small 2x-1\) は原点 \(\small 0\) からの距離が \(\small 5\) の点です。
よって、\(\small 2x-1=\pm5\)
ゆえに、\(\small 2x=-4,\,6\)
したがって、\(\small x=-2,\,3\)
\(\small 2x-1=\pm5\) は、\(\small 2x-1=-5\) と \(\small 2x-1=5\) に分けて計算します。
\(\small \pm\) (プラスマイナス) をつければ良いと丸暗記しないように気をつけてください。
ここを丸暗記してしまうと、このあとの不等式などを乗り越えられなくなってしまうので、しっかりと理解した上で解けるようにしましょう。
次の不等式を解け。
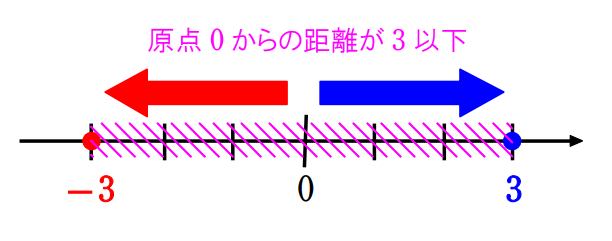
\(\small(1) \vert x-1\vert≦3\)
\(\small(2) \vert 2x-1\vert>5\)
\(\small(1)\) 原点 \(\small 0\) から点 \(\small x-1\) までの距離が \(\small 3\) 以下、
つまり、点 \(\small x-1\) はピンクの斜線部にあるということです。
よって、\(\small -3≦x-1≦3\)
ゆえに、\(\small -2≦x≦4\)
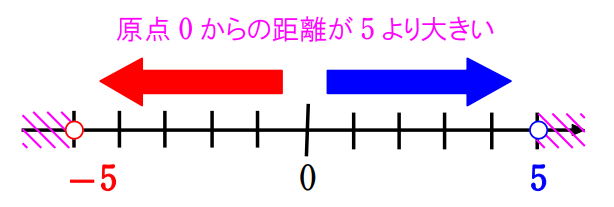
\(\small(2)\) 原点 \(\small 0\) から点 \(\small 2x-1\) までの距離が \(\small 5\) より大きい、
つまり、点 \(\small 2x-1\) は原点 \(\small 0\) から見て \(\small -5\) や \(\small 5\) よりも
遠い点です。
よって、\(\small 2x-1<-5,\,\,5<2x-1\)
ゆえに、\(\small 2x<-4,\,\,6<2x\)
したがって、\(\small x<-2,\,\,3<x\)
\(\small 5<2x-1\) の部分の計算ですが、\(\small x>3\) にしたくなりますか?
これも間違いではないですが、\(\small 3<x\) の方が Best です。
数学の世界では、数を左から小さい順に並べる習わしがあります。つまり、〇<□<△ のように、不等号が右に開くように並べるのが良いとされています。
もう1問、数直線を利用した問題を見ていきましょう。
方程式 \(\small\vert x-1\vert=|2x-3|\) を解け。
\(\small x-1=\pm(2x-3) \)
\(\small x-1=2x-3 \) または \(\small x-1=-(2x-3) \)
\(\small -x=-2 \) または \(\small 3x=4 \)
\(\displaystyle\small x=2,\,\,\frac{4}{3}\)
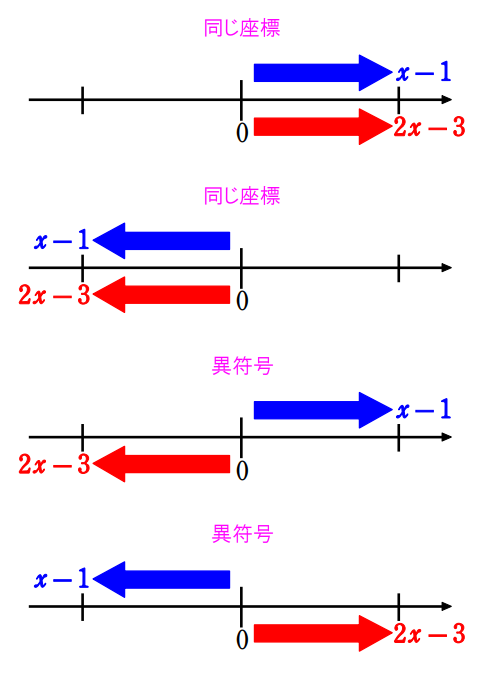
\(\small\vert x-1\vert=|2x-3|\) は、原点 \(\small 0\) から点 \(\small x-1\) までの距離と、原点 \(\small 0\) から点 \(\small 2x-3 \) までの距離が等しいという意味です。
つまり、\(\small x-1\) と \(\small 2x-3 \) は同じ座標となるか、異符号となるかのどちらかです。
同じ座標の場合は、\(\small x-1=2x-3 \)
異符号の場合は、\(\small x-1=-(2x-3) \)
場合分けを利用した絶対値の問題
続いては「場合分けを利用して解く」ものを見ていきましょう。
絶対値の外し方
次の絶対値を解け。
\(\small(1) \vert x-3\vert\)
\(\small(2) |x|+|x-2|\)
\(\small x\) の値によって、絶対値の中身が \(\small 0\) 以上か、\(\small 0\) より小さいかが変わります。
\(\small x\) の値によって、場合分けして絶対値を外しましょう。
\(\small\vert x \vert=
\begin{cases}x\,\,&(x≧0)\\-x&(x<0)\end{cases}\)
\(\small(1)\) 絶対値の中身である \(\small x-3\) が \(\small 0\) 以上か \(\small 0\) より小さいかで場合分けをします。
\(\small(ⅰ) x-3≧0\) つまり \(\small x≧3\) のとき、
(絶対値の中身が \(\small 0\) 以上なので、そのまま外す)
\(\small |x-3|=x-3\)
\(\small (ⅱ) x-3<0\) つまり \(\small x<3\) のとき、
(絶対値の中身が \(\small 0\) より小さいので、\(\small (-1)\) をかけて外す)
\(\small |x-3|=-(x-3)=-x+3\)
\(\small (ⅰ),\,(ⅱ)\) より、
\(\small |x-3|=\begin{cases}x-3&(x≧3)\\-x+3&(x<3)\end{cases}\)
\(\small(2)\) 絶対値の中身である \(\small x\) と \(\small x-2\) が \(\small 0\) になる \(\small x\) つまり \(\small x=0,\,\,2\) を境に場合分けをします。
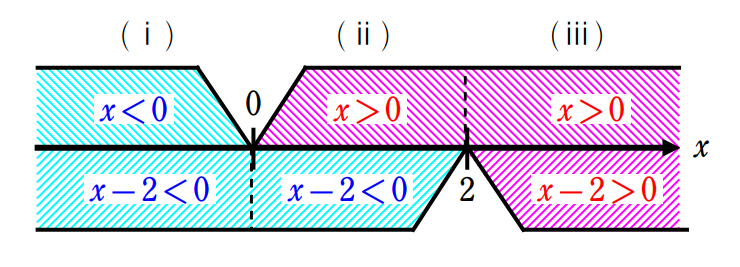
\(\small (ⅰ) x≦0\) のとき、
\(\small |x|+|x-2|=-x-(x-2)=-2x+2\)
\(\small (ⅱ) 0≦x≦2\) のとき、
\(\small |x|+|x-2|=x-(x-2)=2\)
\(\small (ⅲ) 2≦x\) のとき、
\(\small |x|+|x-2|=x+(x-2)=2x-2\)
\(\small (ⅰ)~(ⅲ)\) より、
\(\small |x|+|x-2|=\begin{cases}-2x+2&(x≦0)\\
2&(0≦x≦2)\\2x-2&(2≦x)\end{cases}\)
\(\small (ⅰ)\,(ⅱ)\,(ⅲ)\) における等号の入れ方についてですが、参考書や問題集などでは、
\(\small (ⅰ) x<0\)
\(\small (ⅰ) 0≦x<2\)
\(\small (ⅰ) 2≦x\)
となっていることが多いです。これは上の【公式】の等号の入れ方と同じ考え方です。解答では絶対値の中身が \(\small 0\) になるときは、どちらの場合にも含めて良いという考えで等号を入れています。どちらの等号の入れ方も間違いではないので、好きな方を選んで結構です。
場合分けを利用した絶対値の方程式・不等式
続いて、例題5の考え方を利用した方程式・不等式を紹介します。
次の絶対値を解け。
\(\small(1) |x-1|=2x+7\)
\(\small(2) 2|x|+|x-2|=3\)
例題2のように、数直線を利用しようとしても、\(\small|x-1|=2x-7\) のような式ですと、原点 \(\small 0\) から点 \(\small x-1\) までの距離が \(\small 2x-7\) …?となってしまいます。
この問題は例題5の場合分けの考え方で解いていきましょう。
\(\small(1)\) 絶対値の中身である \(\small x-1\) が \(\small 0\) 以上か \(\small 0\) より小さいかで場合分けをします。
\(\small (ⅰ) x-1≧0\) つまり \(\small x≧1\) のとき、
(絶対値の中身が \(\small 0\) 以上なので、そのまま外す)
\(\small\begin{align} |x-1|=2x+7 \ &\Leftrightarrow \ x-1=2x+7 \\\
& \Leftrightarrow \ \small x=-8\end{align}\)
これは \(\small x≧1\) より不適。
\(\small (ⅱ) x-1<0\) つまり \(\small x<1\) のとき、
(絶対値の中身が \(\small 0\) より小さいので、\(\small (-1)\) をかけて外す)
\(\small\begin{align} |x-1|=2x+7\ &\Leftrightarrow \ -(x-1)=2x+7\\ \ &\Leftrightarrow \ \small x=-2 \end{align}\)
これは \(\small x<1\) を満たす。
\(\small (ⅰ),\,(ⅱ)\) より、\(\small x=-2\)
それぞれの場合で解を求めたあとに、各場合の範囲に当てはまっているか(満たすor不適)を確認し忘れないようにしてください。
\(\small(2)\) 絶対値の中身である \(\small x\) と \(\small x-2\) が \(\small 0\) になる \(\small x\) つまり \(\small x=0,\,\,2\) を境に場合分けをします。

\(\small (ⅰ) x≦0\) のとき、
\(\small\begin{align} 2|x|+|x-2|=3 \ &\Leftrightarrow \ -2x-(x-2)=3\\ &\Leftrightarrow \displaystyle\ x=-\frac{1}{3}\end{align}\)
これは \(\small x≦0\) を満たす。
\(\small (ⅱ) 0≦x≦2\) のとき、
\(\small\begin{align} 2|x|+|x-2|=3 \ &\Leftrightarrow \ 2x-(x-2)=3\\ &\Leftrightarrow \ x=1\end{align}\)
これは \(\small 0≦x≦2\) を満たす。
\(\small (ⅲ) 2≦x\) のとき、
\(\small\begin{align} 2|x|+|x-2|=3 \ &\Leftrightarrow \ 2x+x-2=3\\ &\Leftrightarrow \ \displaystyle x=\frac{5}{3}\end{align}\)
これは \(\small 2≦x\) より不適。
\(\small (ⅰ)~(ⅲ)\) より、\(\displaystyle\small x=-\frac{1}{3},\ 1\)
続いては不等式を見ていきます。
先ほどの方程式の問題が、きちんと理解できていれば、不等式の問題も同じように解けるはずですが、不等式の方が何倍も難しく感じます。
次の絶対値を解け。
\(\small(1) |x-1|≦2x+7\)
\(\small(2) 2|x|+|x-2|>3\)
\(\small(1)\) 絶対値の中身である \(\small x-1\) が \(\small 0\) 以上か \(\small 0\) より小さいかで場合分けをします。
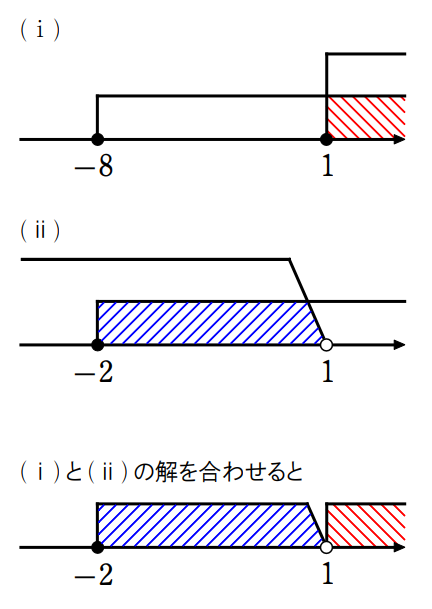
\(\small (ⅰ) x-1≧0\) つまり \(\small x≧1\) のとき、
(絶対値の中身が \(\small 0\) 以上なので、そのまま外す)
\(\small\begin{align} |x-1|≦2x+7\ &\Leftrightarrow \ x-1≦2x+7\\ &\Leftrightarrow \ x≧-8\end{align}\)
これは \(\small x≧1\) より、\(\small x≧1\)
\(\small (ⅱ) x-1<0\) つまり \(\small x<1\) のとき、
(絶対値の中身が \(\small 0\) より小さいので、\(\small (-1)\) をかけて外す)
\(\small\begin{align} |x-1|≦2x+7\ &\Leftrightarrow \ -(x-1)≦2x+7\\ &\Leftrightarrow \ x≧-2\end{align}\)
これは \(\small x<1\) より、\(\small -2≦x<1\)
\(\small (ⅰ),\,(ⅱ)\) より、\(\small x≧1, \ -2≦x<1\)
つまり、\(\small x≧-2\)
\(\small(2)\) 絶対値の中身である \(\small x\) と \(\small x-2\) が \(\small 0\) になる \(\small x\) つまり \(\small x=0,\,\,2\) を境に場合分けをします。
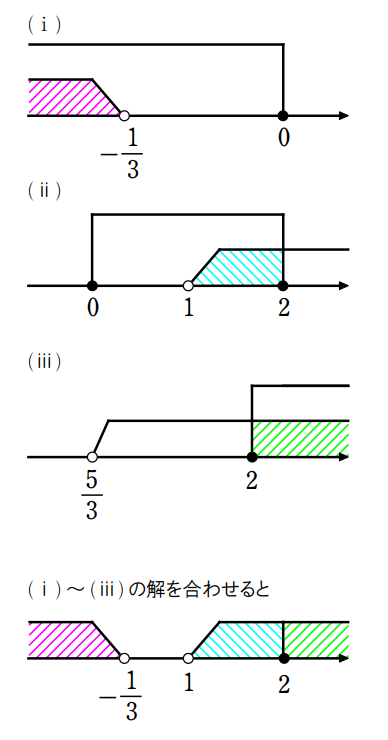
\(\small (ⅰ) x≦0\) のとき、
\(\small\begin{align} 2|x|+|x-2|>3 \ &\Leftrightarrow \ -2x-(x-2)>3\\ &\Leftrightarrow \displaystyle\ x<-\frac{1}{3}\end{align}\)
これは \(\small x≦0\) を満たす。
\(\small (ⅱ) 0≦x≦2\) のとき、
\(\small\begin{align} 2|x|+|x-2|>3 \ &\Leftrightarrow \ 2x-(x-2)>3\\ &\Leftrightarrow \ x>1\end{align}\)
\(\small 0≦x≦2\) より、\(\small 1<x≦2\)
\(\small (ⅲ) 2≦x\) のとき、
\(\small\begin{align} 2|x|+|x-2|>3 \ &\Leftrightarrow \ 2x+x-2>3\\ &\Leftrightarrow \ \displaystyle x>\frac{5}{3}\end{align}\)
\(\small 2≦x\) より、\(\small 2≦x\)
\(\small (ⅰ)~(ⅲ)\) より、\(\displaystyle\small x<-\frac{1}{3},\,\,1<x\)
絶対値はどうでしたか?
例題6や例題7はしっかりと量をこなさないと出来るようにならないので頑張りましょう。
また「数直線を利用して解く問題」と「場合分けを利用して解く問題」の解法が混ざってしまうと、絶対値の問題はできるようになりません。それぞれの例題を理解するだけではなく、例題による違いを比較しながら学習していくことが重要です。
高校1年生、最初の定期テストは絶対値が山場です。しっかりとできるようにして、定期テストで良い点数を勝ち取りましょう!!





コメント