こんにちは。ねこの数式のnanakoです。
数Ⅰと数Aに出てくる『集合』は、本当は簡単なのに、記号がたくさん出てきて分かりづらく感じる単元です。
記号の意味を一つずつ確認して、得意な単元にしてしまいましょう。
集合
集合とは、文字通り『ものの集まり』のことを意味します。高校数学では、基本的に数の集まりを扱うこととなります。
さて、ここから集合を学ぶ上での記号や用語の説明をしていくこととなりますが、厳密な説明を求めるのであれば教科書などを参考にしましょう。
この記事では、少し厳密さにかけたとしても分かりやすさを優先して説明していきたいと思います。
というのも、厳密な説明をするとかなり分かりづらいからです。
では、さっそく見ていきましょう。
集合に出てくる用語と記号の説明!
少し分かりづらかったですかね?下の図を利用した説明も見ていきましょう。
図1のように、海の生き物が集まってできたグループ、集合 \(\small A\) があったとします。
この集合 \(\small A\) には、クジラ、エビ、\(\small \cdots \) がいます。
これを記号で表すと、
クジラ\(\small \in A\)、エビ\(\small \in A\)、\(\small \cdots \)
と表します。

次に集合 \(\small A\) から何匹か選んで新しい集合を作ったのが図2~図4です。
この図2~図4の集合は、集合 \(\small A\) の部分集合と呼びます。
記号で表すと、\(\small B\subset A\)、\(\small C\subset A\)、\(\small D\subset A\) と表します。



ちなみに集合 \(\small D\) は誰もいないので空集合と呼び、 \(\small D=\emptyset\) と表します。
集合 \(\small A\) の部分集合は集合 \(\small B\)、集合 \(\small C\)、集合 \(\small D\) 以外にもたくさんあり、部分集合が何個存在するか求める問題も存在します。これは、『数A場合の数・確率』で紹介したいと思います。
なんとなく用語の意味や記号の使い方が分かりましたか?
使いながら覚えていきましょう。
集合の要素の書き出し!
続いては、集合がどのような要素を含んでいるかをどう表現するか見ていきましょう。
集合にどのような要素が含まれているか表現する方法は、2つあります。
1つ目! \(A=\{\,\)要素①,要素②,要素③,\(\cdots\,\}\)
2つ目! \(B=\{\,\)文字式\(\,|\,\)文字の説明\(\,\}\)
1つ目の表現を『要素書き出し型』、2つ目の表現を『要素説明型』と呼ぶことにします!
(オフィシャルな名称ではないので気をつけてください!!)
次の集合の要素を書き並べて表せ。
\(\small(1) A=\{\,x\,|\,x\,\)は \(\small 6\) の正の約数\(\small \,\}\)
\(\small(2) B=\{\,2n \,|\,0<n<4,\ n\in\mathbb{Z}\,\}\) ただし、\(\small \mathbb{Z} \) は整数全体の集合
『要素説明型』から『要素書き出し型』に書き換える問題ですね。
\(\small(1) A=\{\,\)\(\small x\)\(\small \,|\,\)\(\small x\,\)は \(\small 6\) の正の約数\(\small \,\}\)
まずは、\(\small x\,\)は \(\small 6\) の正の約数の部分から見ていきます。
\(\small 6\) の正の約数は \(\small 1,\,2,\,3,\,6\) ですね。つまり、\(\small x=1,\,2,\,3,\,6\) ということです。
\(\small x\) の部分を見ると、\(\small x\) のまま書き出せという指示となっているので、
\(\small A=\{\,1,\,2,\,3,\,6\,\}\)
\(\small(2) B=\{\,\)\(\small {2n}\)\(\small \,|\,\)\(\small 0<n<4,\ n\in\mathbb{Z}\)\(\small \,\}\) ただし、\(\small \mathbb{Z} \) は整数全体の集合
\(\small n\in\mathbb{Z}\) と \(\small \mathbb{Z} \) は整数全体の集合から、\(\small n\) は整数ということが分かります。
さらに \(\small 0<n<4\) から \(\small n=1,\,2,\,3\) となります。
今回は \(\small 2n\) となっているので、\(\small n\) の値を \(\small 2\) 倍して書き出します。
よって、\(\small B=\{\,2,\,4,\,6\,\}\)
共通部分と和集合
さて、続いては、次の\(\small 2\)つの集合について見ていきます。


\(\small 2\)つの集合に共通している生物がいます。タコですね。
この共通していた生物たちが属する集合を『共通部分』と呼びます。
また、どちらか一方にでもいた生物を集めてくると、エビ,タコ,カニ,イカのグループができます。このように、\(\small 2\)つの集合を合わせた集合を『和集合』と呼びます。
次の図のように集合を〇で表したものを
ベン図と呼びます。
それぞれの〇の中に要素が含まれていると考えてください。
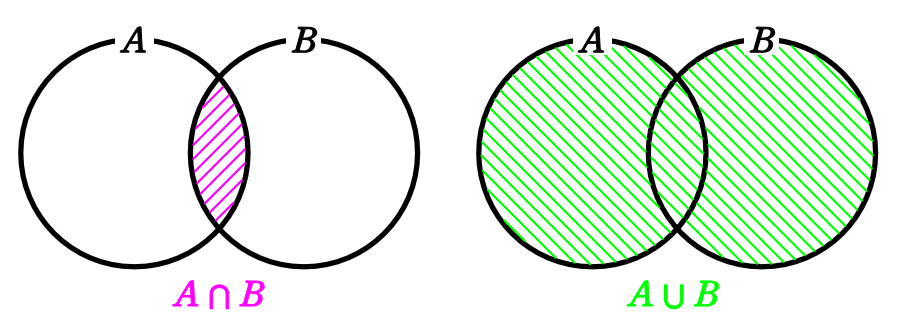
集合 \(\small A\) と集合 \(\small B\) のどちらにも入っている部分、つまり、共通部分を\(\small A\cap B\) と表します。
集合 \(\small A\) と集合 \(\small B\) を合わせた集合、つまり、和集合を \(\small A\cup B\) と表します。
\(\small \cap\) は帽子に見えるので「キャップ」、\(\small \cup\) はカップに見えるので「カップ」なんて呼び方もありますが、「かつ」「または」と呼ぶ方が実用的で良いと思います。(そもそも帽子とカップに見えるのか…という疑問も…)
次の\(\small 2\)つの集合 \(\small A,\,\,B\) について、\(\small A \cap B\) と \(\small A \cup B\) を求めよ。
\(\small(1)\) \(\small A=\{\,x\,|\,x\,\)は \(\small 12\) の正の約数\(\small \,\}\)、\(\small B=\{\,2n \,|\,0≦n≦4,\ n\in\mathbb{Z}\,\}\)
ただし、\(\small \mathbb{Z} \) は整数全体の集合
\(\small(2)\) \(\small A=\{\,x \,|\,0<n<5\,\}\)、\(\small B=\{\,x \,|\,1≦n≦7\,\}\)
\(\small(1)\) それぞれの集合の要素を書き出すと
\(\small A=\{\,1,\,2,\,3,\,4,\,6,\,12\,\}\)
\(\small B=\{\,0,\,2,\,4,\,6,\,8\,\}\)
\(\small 2\) つの集合に共通の要素は、\(\small A \cap B=\{\,2,\,4,\,6\,\}\)
\(\small 2\) つの集合を合わせた要素は、\(\small A \cup B=\{\,0,\,1,\,2,\,3,\,4,\,6,\,8,\,12\,\}\)
\(\small(2)\) この問題では集合の要素を書き出すことができないので、数直線を利用して『要素説明型』で、共通部分と和集合を答えていきたいと思います。
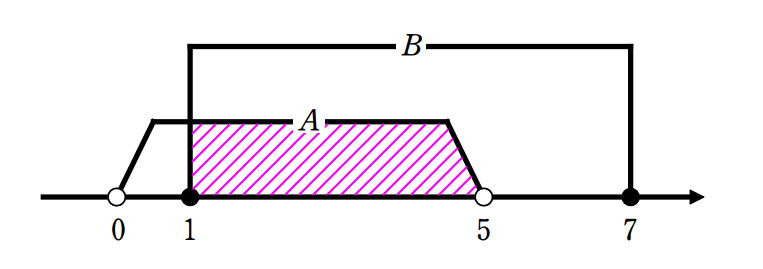
\(\small A\cap B=\{\,x\,|\,1≦x<5\,\}\)
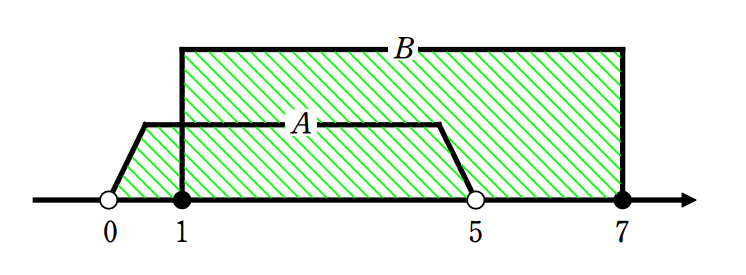
\(\small A\cup B=\{\,x\,|\,0<x≦7\,\}\)
『要素説明型』を利用する際、集合\(=\{\,\)文字式\(\,|\,\)文字の説明\(\,\}\) の文字式の部分は \(\small x\) 以外の文字を使っても良いですが、問題と同じ文字を使うのが普通です。また、\(\small x\) ではなく、\(\small 2x\) などにすることも可能ですが、文字の説明の部分で苦労することとなるので、基本的には、文字式の部分は \(\small x\) としておきましょう。
補集合
さて、一番最初に紹介した「クジラ、エビ、カニ、タコ、イカ、エイ、ヒラメ」からなる集合について、もう一度見てみましょう。
気づいていましたか?一匹だけ哺乳類が混じっていたことに。
そう!クジラですね!!
では、哺乳類以外の生物は何がいるでしょう?

エビ、カニ、タコ、イカ、エイ、ヒラメ・・・だけでしょうか?
だけだと思いましたよね? まだまだ、いますよ!
スズメ! カブトムシ! カノウモビックリミトキハニドビックリササキリモドキ!
え・・・?!
海の生き物じゃなーい!!
って思いましたよね。まぁ、そうですよね。。。
みなさんは、「クジラ、エビ、カニ、タコ、イカ、エイ、ヒラメの集合の中で」という前提で考えてましたよね?(そういう流れで話してましたものね)
このように「○○じゃない集合」を考える際には、外枠が必要となります。その外枠となる集合のことを全体集合といい、通常 \(\small U\) で表します。ベン図では丸ではなく四角で表しましょう。
そして、「○○の集合」に対して「○○じゃない集合」を補集合と呼びます。集合 \(\small A\) の補集合は \(\small \overline{A}\) で表します。
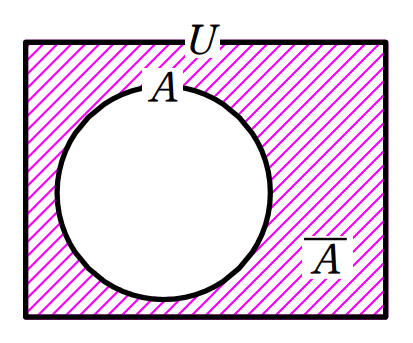
ちなみに、全体集合の補集合は空集合となります。記号で表すと、 \(\small \overline{U}=\emptyset\) となります。
先ほどの{クジラ、エビ、カニ、タコ、イカ、エイ、ヒラメ} を全体集合としたとき、{クジラ、エビ、カニ、タコ、イカ、エイ、ヒラメ} じゃない生物はいないからですね。

全体集合 \(\small U=\{\,n\,|\,n\) は \(\small 10\)以下の自然数 \(\small \}\)、集合 \(\small A=\{\,1,\,2,\,4,\,8\,\}\)、集合 \(\small B=\{\,2,\,4,\,6,\,8,\,10\, \}\) について、次の集合を求めよ。
\(\small(1)\) \(\small \overline{A}\)
\(\small(2)\) \(\small \overline{A}\cap B\)
\(\small U=\{\,\)\(\small1\)\(\small,\,\)\(\small2\)\(\small,\,3,\,\)\(\small4\)\(\small,\,5,\,6,\,7,\,\)\(\small8\)\(\small,\,9,\,10\,\}\)
\(\small(1)\) 集合 \(\small A=\{\,\)\(\small1,\,2,\,4,\,8\)\(\small\,\}\) に含まれない要素を答えればよいので、
\(\small \overline{A}=\{\,3,\,5,\,6,\,7,\,9,\,10\,\}\)
\(\small(2)\) 集合 \(\small A\) に含まれない要素、かつ、集合 \(\small B\) に含まれる要素を答えれば良いのですが、分かりづらくないですか?\(\small (1)\) の答えを利用しましょう。
\(\small \overline{A}=\{\,3,\,5,\,\)\(\small 6\)\(\small ,\,7,\,9,\,\)\(\small10\)\(\small\,\}\) と、
\(\small B=\{\,2,\,4,\,\)\(\small6\)\(\small,\,8,\,\)\(\small10\)\(\small\, \}\)
の共通の要素を求めればよいので、\(\small \overline{A} \cap B=\{\,\)\(\small6,\,10\)\(\small\,\}\)
\(\small \overline{A} \cap B\) や \(\small A \cup \overline{B}\) など補集合を含んだ共通部分や和集合を求める際は、\(\small (1)\) のように、補集合に含まれる要素を先に求めてから、共通部分や和集合を求めると間違えづらいです。
次は要素が書き出せないパターンです。
実数全体の集合を全体集合とする。集合 \(\small A=\{\,x\,|\,1≦x<3\,\}\) の補集合 \(\small \overline{A}\) を求めよ。
集合 \(\small A\) を数直線に図示すると、次の図の黒い斜線部となります。これ以外の部分が \(\small \overline{A}\) となります。つまり、ピンクの斜線部を答えていきましょう。
\(\small \overline{A}=\{\,x\,|\,x<1,\,\,3≦x\,\}\)
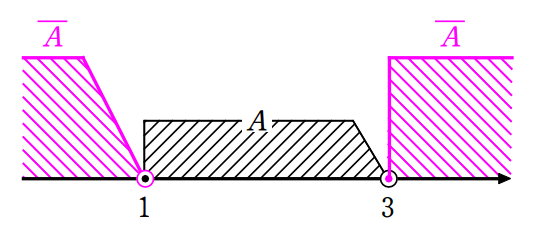
\(\small x=1\) は集合 \(\small A\) に含まれているので、補集合 \(\small \overline{A}\) には含まれません。逆に、\(\small x=3\) は集合 \(\small A\) に含まれていないので、補集合 \(\small \overline{A}\) に含まれます。
ド・モルガンの法則
「オシリカジリムシ」ってご存じですか?
「おしりかじり虫」ではないですよ。オシリカジリムシ科、オシリカジリムシ属のオシリカジリムシです。
実は、「オシリカジリムシ」とは、2022年1月24日に発表された新種の小型甲殻類で、発見者である是枝さんが命名したものです。あごを使ってかじりつくような姿から、NHK「みんなのうた」のキャラクター「おしりかじり虫」にちなんで名付けられました。
このように何か新しいものを発見した際、発見者が命名することがよくあります。
ということで、「オーガスタス・ド・モルガン」さんが発見した便利な法則、それが!!
ド・モルガンの法則・・・えっと・・・
もう一度言います!!
ド・モルガンの法則!!
そう、モルガンさんは、発見した法則に自分の名前をつけちゃったんですよ。
名前はさておき、便利な法則なのでみていきましょう。
\(\small (1) \overline{A\cap B}=\overline{A}\cup\overline{B}\)
\(\small (2) \overline{A\cup B}=\overline{A}\cap\overline{B}\)
図を利用して仕組みを理解してみたいと思います。
\(\small A \cap B\) と \(\small A \cup B\) をベン図で表すと図5となります。
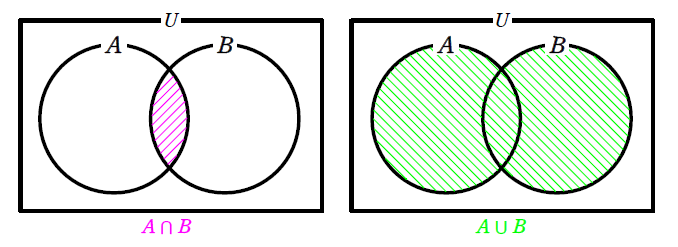
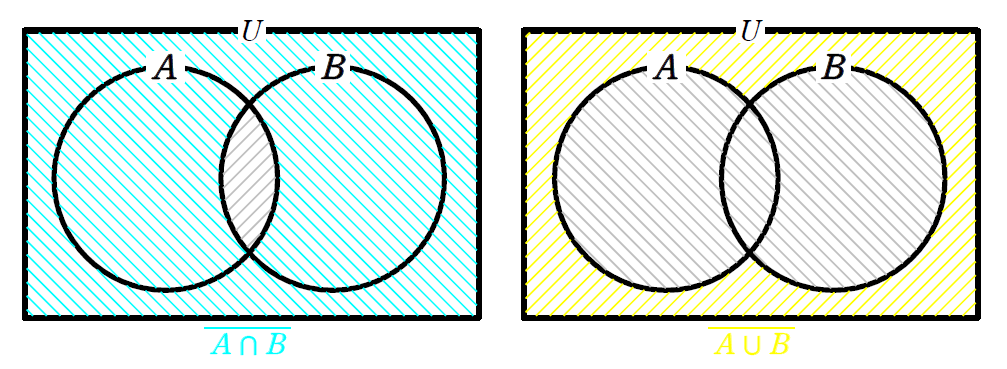
図5のそれぞれのベン図において、斜線部以外が、\(\small \color{#00f0f0}{\overline{A\cap B}}\) と \(\small \color{#f0f000}{\overline{A\cup B}}\) なので、図6の色のついた部分となります。
次に、\(\small \overline{A}\) と \(\small \overline{B}\) をベン図にします。
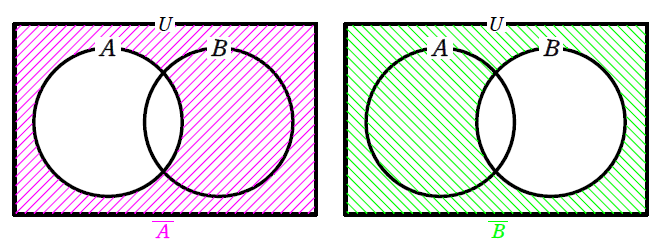
図7において、ピンクの斜線部とグリーンの斜線部を足し合わせた部分が \(\small \color{#00f0f0}{\overline{A}\cup\overline{B}}\) であり、\(\small 2\)つの斜線部に共通している部分が \(\small \color{#f0f000}{\overline{A}\cap\overline{B}}\) であるので、図8のようなベン図になります。
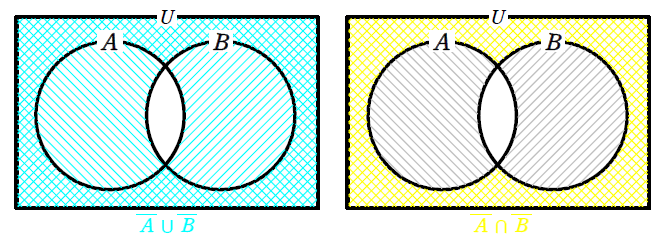
図6と図8を並べて比較すると


\(\small \color{#00f0f0}{\overline{A\cap B}=\overline{A}\cup\overline{B}}\)、\(\small \color{#f0f000}{\overline{A\cup B}=\overline{A}\cap\overline{B}}\) となることが分かりましたね。
全体集合 \(\small U=\{\,n\,|\,n\) は \(\small 10\)以下の自然数 \(\small \}\)、集合 \(\small A=\{\,1,\,2,\,4,\,8\,\}\)、集合 \(\small B=\{\,2,\,4,\,6,\,8,\,10\, \}\) について、次の集合を求めよ。
\(\small(1)\) \(\small \overline{A}\)
\(\small(2)\) \(\small \overline{A}\cap B\)
\(\small(3)\) \(\small A\cup \overline{B}\)
\(\small (1)\) と \(\small (2)\) は例題3と同じ問題です。
\(\small U=\{\,\)\(\small1\)\(\small,\,\)\(\small2\)\(\small,\,3,\,\)\(\small4\)\(\small,\,5,\,6,\,7,\,\)\(\small8\)\(\small,\,9,\,10\,\}\)
\(\small(1)\) 集合 \(\small A=\{\,\)\(\small1,\,2,\,4,\,8\)\(\small\,\}\) に含まれない要素を答えればよいので、
\(\small \overline{A}=\{\,3,\,5,\,6,\,7,\,9,\,10\,\}\)
\(\small(2)\) 集合 \(\small A\) に含まれない要素、かつ、集合 \(\small B\) に含まれる要素を答えれば良いのですが、分かりづらくないですか?\(\small (1)\) の答えを利用しましょう。
\(\small \overline{A}=\{\,3,\,5,\,\)\(\small 6\)\(\small ,\,7,\,9,\,\)\(\small10\)\(\small\,\}\) と、
\(\small B=\{\,2,\,4,\,\)\(\small6\)\(\small,\,8,\,\)\(\small10\)\(\small\, \}\)
の共通の要素を求めればよいので、\(\small \overline{A} \cap B=\{\,\)\(\small6,\,10\)\(\small\,\}\)
\(\small (3)\) ド・モアブルの定理より、 \(\small \begin{align} \overline{(\overline{A} \cap B)}&=\overline{(\overline{A})}\cup \overline{B}\\
&=A\cup \overline{B}\end{align}\)
よって、\(\small A\cup \overline{B}\) は \(\small \overline{A} \cap B=\{\,\)\(\small6,\,10\)\(\small\,\}\) の補集合なので、
\(\small A\cup \overline{B}=\{\,1,\,2,\,3,\,4,\,5,\,7,\,8,\,9\,\}\)
\(\small A \cup \overline{B}\) が \(\small \overline{A} \cap B\) の補集合であることに気づけると、ド・モルガンの法則が使える問題でした。気づけなかった場合は、\(\small (3)\) も \(\small (2)\) と同じように解けば解けます。ちなみに、\(\small \overline{(\overline{A})}\) は、\(\small A\) じゃない集合じゃない集合…、つまり、2重否定となり、\(\small A\) となります。
集合の要素の個数
数学では、求めたいものなどを日本語のまま計算するのは現実的ではないので、文字や記号で表すことがよくあります。今回は集合の要素の個数の表現の仕方を見ていきたいと思います。
集合の要素の個数の表し方
集合\(\small \,A\,\)の要素の個数を\(\small \,n(A)\,\)と表す。
\(\small n\,\)は英語の number の頭文字で、集合の要素の個数は、\(\small\,n(\)集合の名前\(\small)\,\)という形で表します。
続いては、集合の要素の個数を扱う上で、重要な公式を紹介します。
\(\small n(A\cup B)=n(A)+n(B)-n(A\cap B)\)
ピンとこないと思うので、具体例でみていきましょう。
スマブラをやったことがある人が\(\small\,50\,\)人、ポケモンをやったことがある人が\(\small\,30\,\)人、どちらもやったことがある人が\(\small\,10\,\)人いました。さて、少なくともどちらかはやったことがあるのは何人でしょうか?
どちらかはやったことがある人数を求めるために、スマブラをやったことがある人数とポケモンをやったことがある人数を足してみましょう。
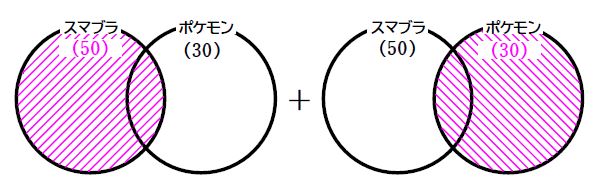
どちらもやったことがある人を2回数えていることに気づきますか?
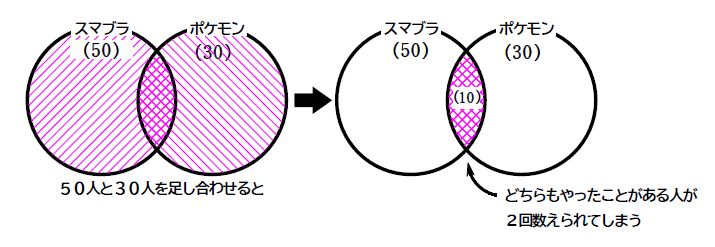
という事で、2回数えてしまったのを調整すれば良いので、どちらかはやったことがある人数は、\(\small 50+30-10=70\) 人だという事が分かりました。

つまり、\(\small n(A\cup B)=n(A)+n(B)-n(A\cap B)\) が成り立つというわけです。
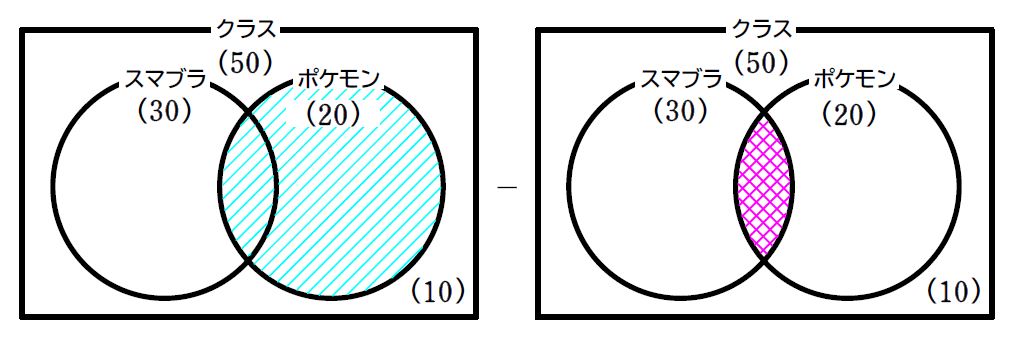
ある\(\small\,50\,\)人のクラスには、スマブラをやったことがある人が\(\small\,30\,\)人、ポケモンをやったことがある人が\(\small\,20\,\)人いました。どちらもやったことがない人は\(\small\,10\,\)人いました。このとき、次の問いに答えよ。
\(\small (1)\) どちらもやったことがあるのは何人か答えよ。
\(\small (2)\) ポケモンだけしかやったことがないのは何人か答えよ。
今回の問題もベン図を使うと解きやすいのです。まずは\(\small \,(1)\,\)から
① 問題文をベン図にするとこのようになります。
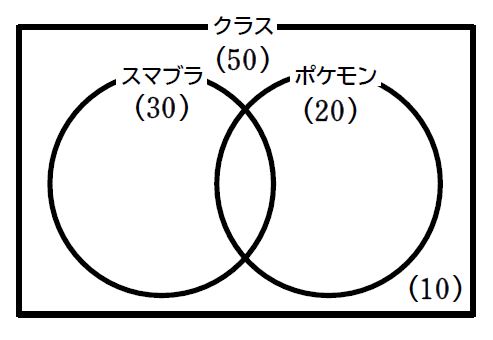
② \(\small(1)\,\)で求める部分はピンクの網線部です。
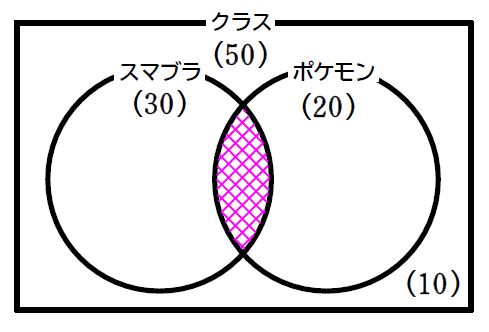
③ 公式を利用したいので、少なくともどちらかをやったことがある人たちの人数を求めます。
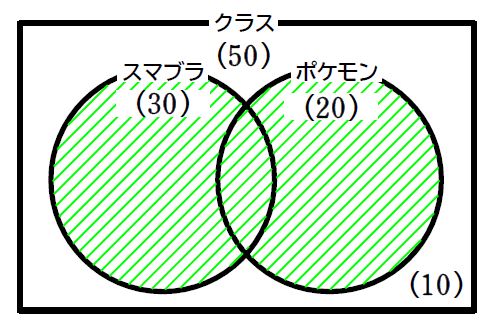
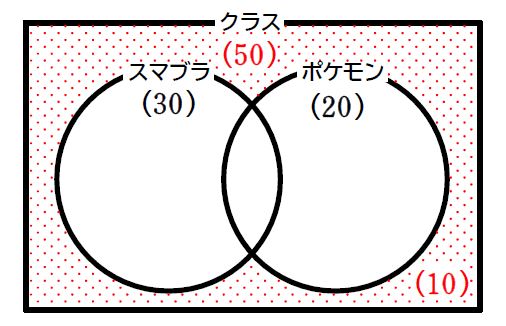
④ 全体からどちらもやったことがない人を除けば良いので、\(\small \color{red}{50}-\color{red}{10}=\color{#64dc64}{40}\,\)人です。
⑤ 求める人数を\(\small \,x\,\)として、公式を使うと、\(\small 40=30+20-x \Leftrightarrow x=\color{magenta}{10}\,\)人
続いて、\(\small (2)\,\)です。
⑤ \(\small(2)\,\)の求めたい部分は青い斜線部です。
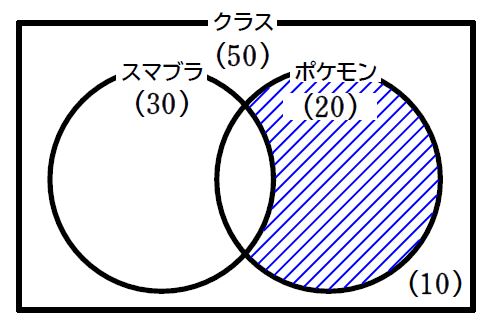
⑥ 水色の斜線部からピンクの斜線部を引いて求めます。つまり、\(\small \color{#64f0f0}{20}-\color{magenta}{10}=\color{blue}{10}\,\)人
以上で、\(\small (1),\ (2)\,\)の答えは求まったわけですが、模範解答とするのはちょっと心苦しいです。やはり模範解答は\(\small \,n(A)\,\)などの表し方を利用して書いておきます。
\(\small \,50\,\)人のクラスを全体集合\(\small\,U\,\)とし、スマブラ、ポケモンをやったことがある人の集合をそれぞれ \(\small A,\ B\,\)とする。このとき、\(\small n(U)=50,\ n(A)=30,\ n(B)=20,\ n\left(\overline{A\cup B}\right)=10\,\)である。
\(\small\begin{align} (1) n(A\cup B)&=n(U)-n\left(\overline{A\cup B}\right)\\&=50-10\\&=40\end{align}\)
\(\small n(A\cup B)=n(A)+n(B)-n(A\cap B)\) より、
\(\small 40=30+20-n(A\cap B) \Leftrightarrow n(A\cap B)=10\)
よって、\(\small 10\,\)人。
\(\small \begin{align} (2) n\left(\overline{A}\cap B\right)&=n(B)-n(A\cap B)\\&=30-10\\&=20 \end{align}\)
よって、\(\small 20\,\)人。
ちゃんとした記述はとにかく分かりづらいですよね。集合の問題は、定期テストでは答えのみの場合が多いと思います。\(\small n(A)\,\)などの表し方で練習するかは定期テストでの出題のされ方を踏まえて判断でも良いとは思います。
3集合の要素の個数
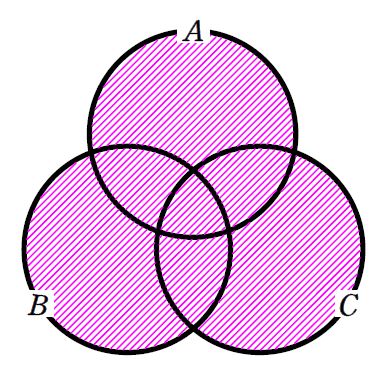
\(\small n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)\)
\(\small n(A\cup B\cup C)\) は次の図のピンクの斜線部になり、この部分の求め方を考えていきましょう。
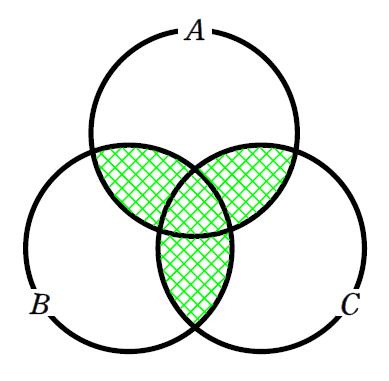
\(\small n(A)+n(B)+n(C)\) とすると、次の図の緑の網線部を多く数えていることとなります。そのため、\(\small n(A\cap B)+n(B\cap C)+n(C\cap A)\) を引くこととなります。
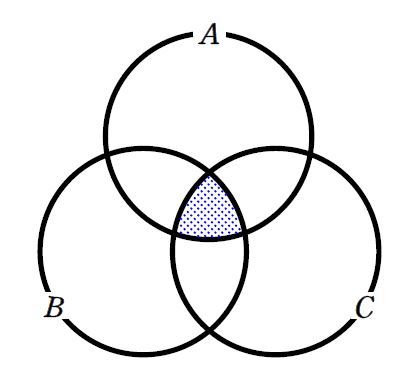
次の図の青い打点部は、\(\small n(A)+n(B)+n(C)\) で3回数えていましたが、\(\small n(A\cap B)+n(B\cap C)+n(C\cap A)\) を引いたことにより、1回も数えていないこととなりました。なので、最後に1回足す必要があります。
よって、\(\small n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)\) となるわけです。
ある\(\small\,50\,\)人のクラスには、ピカチューを捕まえたことがある人が\(\small \,20\,\)人、イーブイを捕まえたことがある人が\(\small \,18\,\)人、コイキングを捕まえたことがある人が\(\small \,18\,\)人、ピカチューとイーブイを捕まえたことがある人が\(\small \,5\,\)人、イーブイとコイキングを捕まえたことがある人が\(\small \,7\,\)人、コイキングとピカチューを捕まえたことがある人が\(\small \,8\,\)人、どれも捕まえたことがない人が\(\small \,11\,\)人いました。すべて捕まえたことがある人は何人か答えよ。
- step1どれか1つでも捕まえたことがある人の人数を求める
(クラスの人数)\(\small -\)(どれも捕まえたことがない人の人数)
- step2公式を使う
\(\small n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)\) に代入
- step3すべて捕まえたことがある人の人数を求める
step2で立てた方程式を解く
クラス\(\small\,50\,\)人を全体集合とする。ピカチュー、イーブイ、コイキングを捕まえたことがある人の集合をそれぞれ\(\small \,A,\ B,\ C\,\)とする。このとき、\(\small n(A)=20,\ \)\(\small n(B)=18,\ \)\(\small n(C)=18,\ \)\(\small n(A\cap B)=5,\ \)\(\small n(B\cap C)=7,\ \)\(\small n(C\cap A)=8,\ \)\(\small n\left(\overline{A\cup B\cup C}\right)=11\)
どれか1つでも捕まえたことがある人の人数は、
\(\small \begin{align}n(A\cup B\cup C)&=n(U)-n\left(\overline{A\cup B\cup C}\right)\\&=50-11\\&=39\end{align}\)
\(\small n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)\) より、
\(\small \begin{align} &39=20+18+18-5-7-8+n(A\cap B\cap C)\\
\Leftrightarrow \ &n(A\cap B\cap C)=3\end{align}\)
よって、すべて捕まえたことがある人は、\(\small 3\,\)人。
まとめ!
どうでしたか?集合は?
記号の多さなどで見た目以上に難しく感じる単元でした。言い方を変えれば、記号さえ覚えてしまえば意外と難しくないということなので、あきらめずに一つずつ覚えていきましょう。





コメント