こんにちは。ねこの数式のnanakoです。
中学校のときにも2次関数は扱いましたね。
2次関数をグラフにしたものが放物線でした。中学校のときは放物線の頂点は原点にありましたが、高校では平行移動したものも扱っていきます。
この2次関数の内容は、これから数学を学ぶ上で色んな単元で使っていくものです。しっかりと理解して、これからの数学人生に弾みをつけましょう!
2次関数のグラフの進化!
関数
そもそも関数って何ですかね?
2つの変数\(\small \,x,\ y\,\)について、\(\small x\,\)の値を定めると、\(\small y\,\)の値が定まるとき、\(\small y\,\)は\(\small \,x\,\)の関数という。
イメージとしてはこれです。

おーい、お茶 ・・・ ではないですよ。
自動販売機です!
自動販売機は、押すボタンによって出てくる飲み物が変わりますよね。
押したボタンの情報が変数\(\small\,x\)、出てきた缶ジュースが変数\(\small \,y\)、そして、自動販売機が関数と考えればOKです。
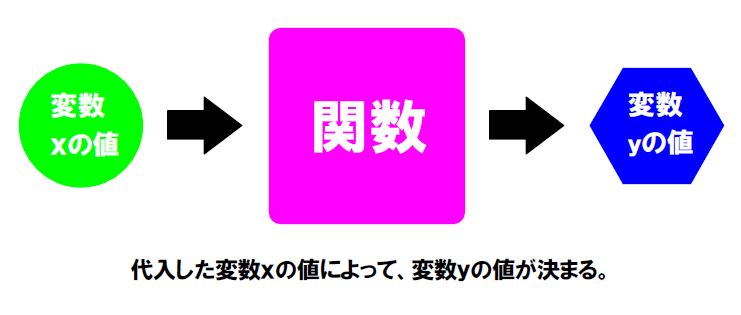
関数のイメージはつかめましたか?
続いては次の文章を見てください。
関数\(\small \,y=2x^2+3x-1\,\)に\(\small\ x=1\,\)を代入すると、\(\small y=4\)
関数\(\small \,y=2x^2+3x-1\,\)に\(\small\ x=2\,\)を代入すると、\(\small y=13\)
関数\(\small \,y=2x^2+3x-1\,\)に\(\small\ x=3\,\)を代入すると、\(\small y=26\)
関数\(\small \,y=2x^2+3x-1\,\)に\(\small\ x=5\,\)を代入すると、\(\small y=64\)
\(\small \vdots\)
では次に、これを写してください・・・
『めんどくさいな~』って思いましたよね? ですよね~ ですよね~
数学を研究してた人たちも同じことを思ったんですよ~
そこで、楽する方法を考えました。それが、\(\small f(x)\) です。
\(\small f\) は fanction の頭文字の f で、カッコの中の \(\small x\) は「\(\small x\,\)で表された式」という意味です。
つまり、\(\small f(x)\) は \(\small x\) の関数という意味です。
さっそく、\(\small f(x)\) を用いて、先ほどの文章を書きなおしてみます。
関数 \(\small f(x)=2x^2+3x-1\) について、 ………①
\(\small y=f(1)=4\) ………②
\(\small y=f(2)=13\)
\(\small y=f(3)=26\)
\(\small y=f(5)=64\)
\(\small \vdots\)
ずいぶんとコンパクトになりましたね。細かく説明していきます。
\(\small f(x)=2x^2+3x-1\) は、『 \(\small 2x^2+3x-1\) に \(\small f(x)\) というあだ名をつけますね!』という意味。
『本名である \(\small 2x^2+3x-1\) を何度も書くのが面倒なので、あだ名である \(\small f(x)\) を使って書くよ』っていう宣言です。
\(\small f(\color{magenta}{x})\) の \(\small \color{magenta}{x}\) の部分が \(\small \color{magenta}{1}\) となっています。これは『 \(\small f(\color{magenta}{x})\) に \(\small \color{magenta}{x=1}\) を代入するよ』っていう意味です。
つまり、『関数\(\small \,y=2x^2+3x-1\,\)に\(\small\ x=1\,\)を代入すると、\(\small y=4\)』の代わりとなる式です。
なんとなくイメージできましたかね。今後、よく使うので覚えておきましょう。
グラフの方程式
中学校のときに『放物線の方程式』って言葉は聞いたことがありますか?
意外と重要な話になるので、読み飛ばさないでくださいね!
「2次関数をグラフにしたものが放物線」は先ほど、話題に上がりましたね。これを別の表現で説明すると「放物線の方程式は2次関数となる」となります。
つまり、「放物線 \(\small \color{red}{y=ax^2}\)」の \(\small \color{red}{y=ax^2}\) の部分です。
そして、もともと放物線(=2次関数のグラフ)を描くとき、\(\small \color{red}{y=ax^2}\) を満たす点を集めてきたものだったことから、放物線の方程式というのは、放物線上のどの点でも成り立つ関係式の事です。
まとめると
グラフの方程式とは、グラフ上のすべての点で成り立つ関係式のこと。
高校で習う2次関数
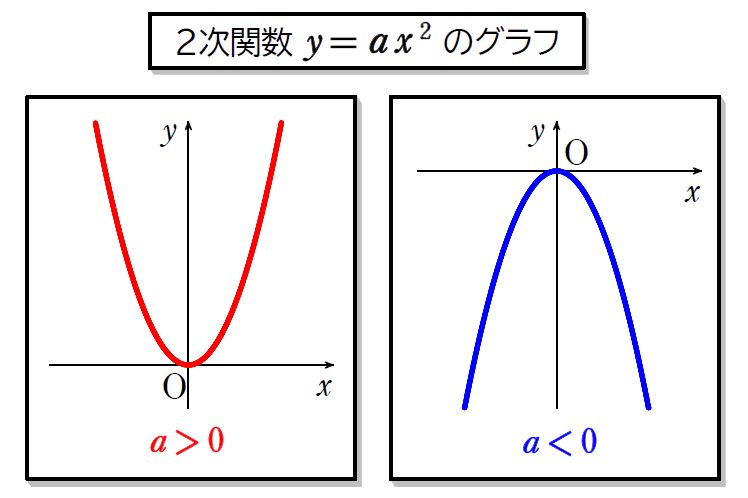
中学校のときに習った2次関数のグラフは、頂点が原点にあるものだけでした。\(\small y=ax^2\) の\(\small \ a\ \)の値が正のときと負のときでグラフの向きが変わりましたね。
\(\small \ a\ \)の値が正のとき、グラフが下に出っ張っている状況を、「下に凸のグラフ」といいます。
\(\small \ a\ \)の値が負のとき、グラフが上に出っ張っている状況を、「上に凸のグラフ」といいます。
では、これらのグラフを平行移動したものを見ていきましょう。
3つの2次関数 \(\small y=x^2+2\),\(\small y=(x-1)^2\),\(\small y=(x-1)^2+2\) のグラフの特徴を調べていきます。
まずは、\(\small y=x^2\) と \(\small y=x^2+2\) の\(\small \,y \)座標を調べて、グラフがどう変化するか見てみましょう。
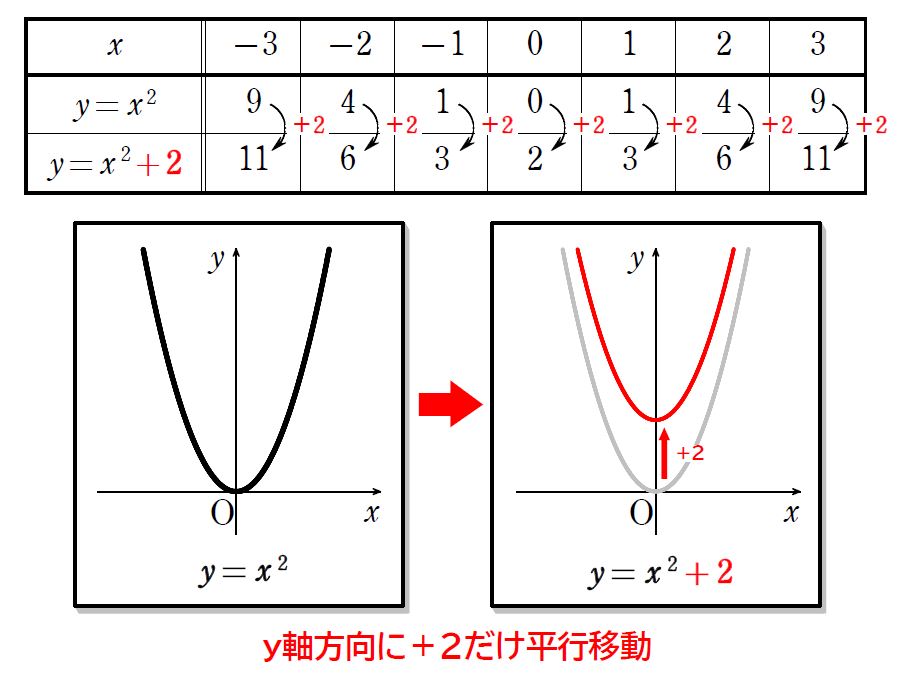
関数が \(\small y=x^2\color{red}{+2}\) となると、\(\small y=x^2\) のグラフを上に \(\small +2\) 平行移動されることが分かりました。この「上に\(\small \,+2\,\)平行移動する」ことを「\(\small y\,\)軸方向に\(\small \,+2\,\)だけ平行移動する」と表現します。
次に \(\small y=x^2\) と \(\small y=(x-1)^2\) の\(\small \,y \, \)座標を調べて、グラフがどう変化するか見てみましょう。
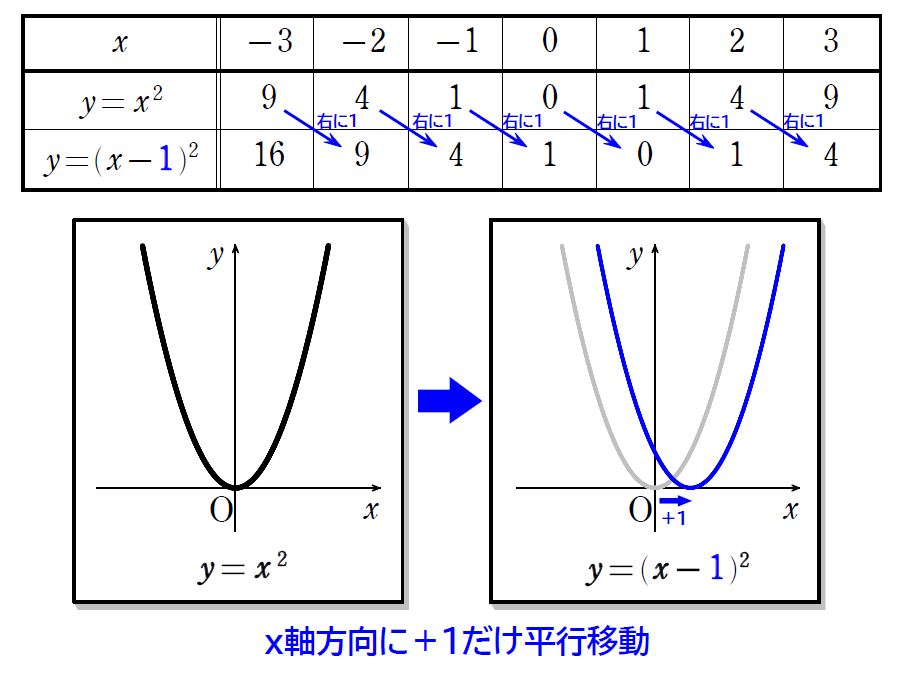
関数が \(\small y=(x-\color{blue}{1})^2\) となると、\(\small y=x^2\) のグラフを右に \(\small +1\) 平行移動されることが分かりました。この「右に\(\small \,+1\,\)平行移動する」ことを「\(\small x\,\)軸方向に\(\small \,+1\,\)だけ平行移動する」と表現します。
最後に、\(\small y=(x-1)^2+2\) のグラフを見ていきましょう。
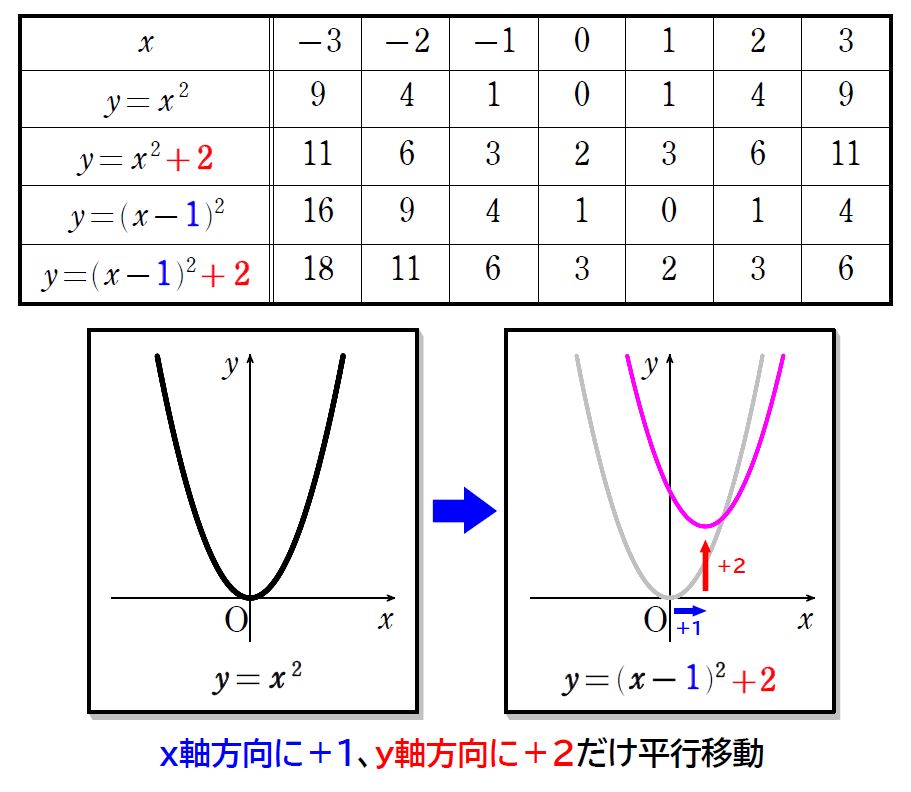
\(\small y=(x-1)^2+2\) のグラフは、\(\small y=x^2\) のグラフを\(\small x\,\)軸方向に\(\small \,+1\,\)、\(\small y\,\)軸方向に\(\small \,+2\,\)だけ平行移動されることが分かりました。
これらの内容をふまえて公式を作りたいと思います。
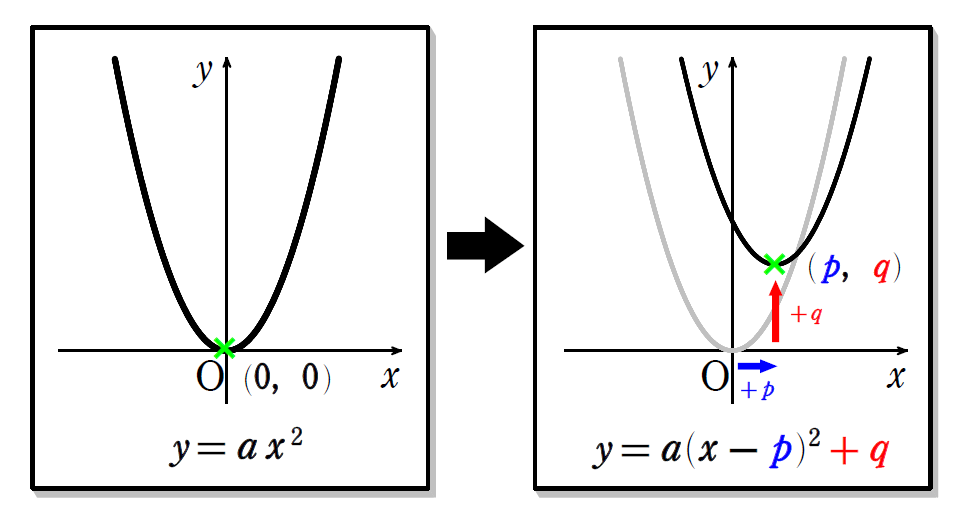
2次関数 \(\small y=a(x-p)^2+q\) のグラフの特徴
\(\small (1)\) 2次関数 \(\small y=ax^2\) のグラフを\(\small \,x\,\)軸方向に\(\small \,+p\)、\(\small y\,\)軸方向に\(\small \,+q\,\)だけ平行移動したもの。
\(\small (2)\) 頂点の座標:\(\small (p,\ q)\)、軸の方程式:\(\small x=p\)
\(\small (3)\) \(\small a>0\) のとき下に凸、\(\small a<0\) のとき上に凸のグラフ
放物線 \(\small y=ax^2\) の頂点は原点 \(\small (0,\ 0)\) でしたね。
放物線 \(\small y=a(x-p)^2+q\) は、放物線 \(\small y=ax^2\) を\(\small \,x\,\)軸方向に\(\small \,+p\)、\(\small y\,\)軸方向に\(\small \,+q\,\)だけ平行移動したものなので、頂点の座標は\(\small \ (p, \ q)\) となります。
軸の方程式という新しい言葉が出てきました。
軸とは対称軸のことで『頂点を通る\(\small \,y\,\)に平行な直線』のことを指します。
2次関数 \(\small y=ax^2\) のグラフは、左右対称でしたね。どこで対称だったかというと、\(\small y\,\)軸でした。\(\small \,y\,\)軸上はどこでも\(\small \,x\,\)座標が\(\small \,0\,\)です。よって、\(\small y\,\)軸は直線 \(\small x=0\) と表せます。これが、軸の方程式です。
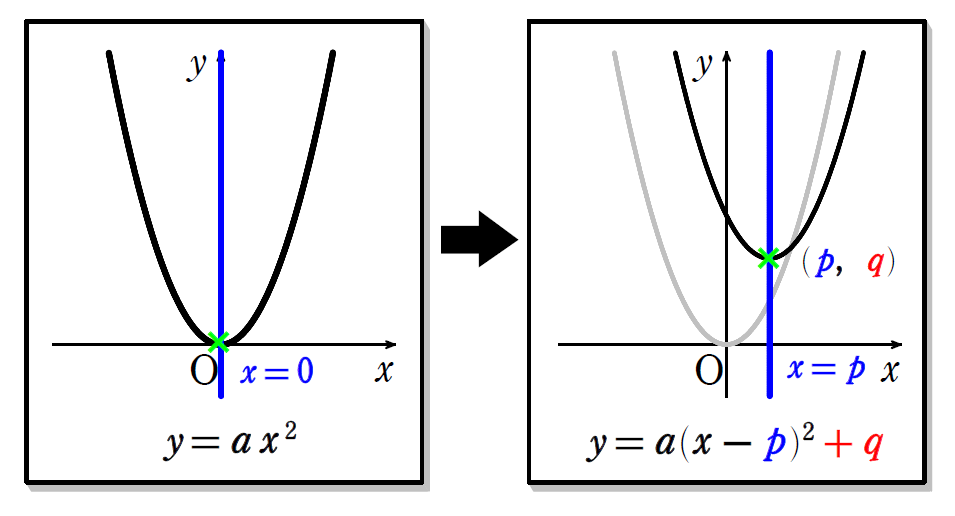
2次関数 \(\small y=a(x-p)^2+q\) の軸の方程式は、頂点の座標が \(\small (p,\ q)\) であることから、\(\small x=p\) となるわけです。
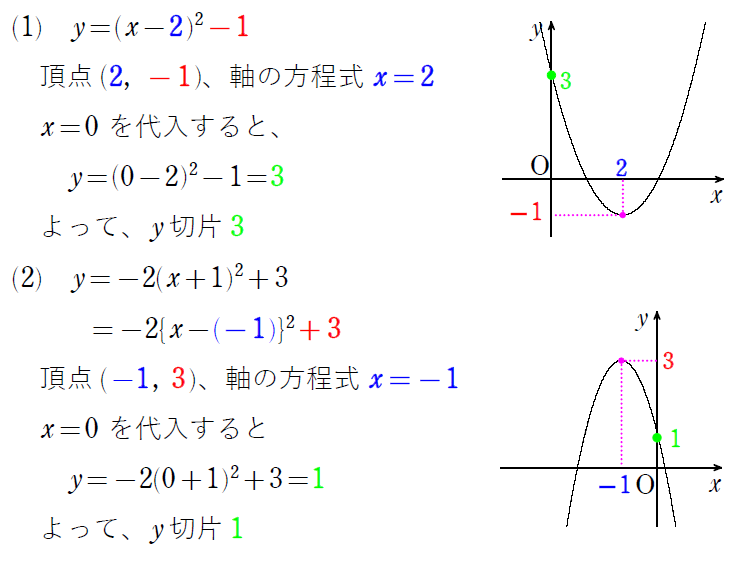
次の放物線の頂点と軸の方程式を求め、グラフをかけ。
\(\small(1) y=(x-2)^2-1\)
\(\small(2) y=-2(x+1)^2+3\)
続いては、放物線 \(\small y=x^2-4x+5\) を図示してみたいと思います。
図示してみたいと思います???
できるかーい!!
式が先ほど習った形から展開されてしまっています。
図示するためには、展開する前がどんな式だったのか調べる必要があります。そこで使うのが、中学校のときに習った『平方完成』です。
では、平方完成の仕方を詳しくみていきましょう!
まずは先ほどの \(\small y=x^2-4x+5\) を平方完成してみます。

続いては、\(\small y=2x^2+4x+1\) の平方完成の仕方をみてみます。

念のため、例題としてもう一度平方完成してみましょう。
放物線 \(\small y=-x^2+6x-2\) の頂点を求めよ。
\(\small \begin{align} y&=-(x^2-6x)-2\\ &=-(x-3)^2-(-3)^2\times (-1)-2\\
&=-(x-3)^2+7 \end{align}\)
よって、頂点は \(\small (3,\ 7) \)
平行移動と対称移動をしてみる!
平行移動
\(\small y=x^2+2\) のグラフは \(\small y=x^2\) のグラフを\(\small \ y \ \)軸方向に\(\small \,+2 \, \)だけ平行移動したものでした。\(\small y=x^2+2\) は \(\small y-2=x^2\) と変形できます。
つまり、\(\small \color{red}{y}=x^2\) と \(\small \color{red}{y-2}=x^2\) のグラフの比較から、\(\small \color{red}{y} \ \)の部分が\(\small \ \color{red}{y-2} \ \)に変化すると、グラフの形を変化させずに\(\small \ y \ \)軸方向に\(\small \, \color{red}{+2} \ \)だけ平行移動することが分かりました。
\(\small y=\color{blue}{x}^2\) と \(\small y=(\color{blue}{x-1})^2\) のグラフの比較から、\(\small \color{blue}{x} \ \)の部分が\(\small \ \color{blue}{x-1} \ \)に変化すると、グラフの形を変化させずに\(\small \ x \ \)軸方向に\(\small \, \color{blue}{+1} \ \)だけ平行移動することが分かりました。
今回はこれを公式化してみたいと思います。
放物線 \(\small y=f(x)\) を\(\small \, x \, \)軸方向に\(\small \, p \)、\(\small y \, \)軸方向に\(\small \, q \,\)だけ平行移動した放物線の方程式は、\(\small \color{red}{y-q}=f(\color{blue}{x-p}) \)となる。
公式とするために\(\small \, f(x) \, \)を利用しましたが、分かりづらいと思うので、別の説明の仕方をします。
\(\small x \, \)軸方向に\(\small \, p \, \)だけ平行移動したいとき
→\(\small \ x \ \)を\(\small \ x-p \ \)に変える。
\(\small y \, \)軸方向に\(\small \, q \,\)だけ平行移動したいとき
→\(\small \ y \ \)を\(\small \ y-q \ \)に変える。
実際に使ってみましょう。
放物線 \(\small y=2x^2+4x+1\) を\(\small \, x \, \)軸方向に\(\small \,-2 \)、\(\small y \,\)軸方向に\(\small \, 3 \,\)だけ平行移動した放物線の方程式を求めよ。
\(\small x \, \)を\(\small \, x-(-2) \)、つまり、\(\small x+2 \)、
\(\small y \, \)を\(\small \, y-3 \, \)に変えれば良いので、
\(\small \begin{align} &y-3=2(x+2)^2+4(x+2)+1\\ \Leftrightarrow \ &y-3=2x^2+12x+17\\
\Leftrightarrow \ &y=2x^2+12x+20 \end{align}\)
気づきましたか?「放物線の方程式を求めよ」という問題文に対して、平方完成した形ではなく、展開した形を解にしています。「放物線の方程式を求めよ」や「2次関数を求めよ」という問題文に対しての解は、平方完成した形でも展開した形でもOKです。ただ、\(\small y-3=2(x+2)^2+4(x+2)+1 \) のような中途半端な形はNGなので気をつけてください。
別解として、次のような解答もあります。
\(\small \begin{align} y&=2x^2+4x+1\\ &=2(x+1)^2-1\end{align}\)
よって、平行移動前の放物線の頂点の座標は\(\small \,(-1,\ -1) \)
これを\(\small \, x \, \)軸方向に\(\small \,-2 \)、\(\small y \,\)軸方向に\(\small \, 3 \,\)だけ平行移動した放物線の頂点の座標は\(\small \,(-3,\ 2) \)
平行移動しただけなので、\(\small x^2 \, \)の係数は変化しないので、求める放物線の方程式は、\(\small y=2(x+3)^2+2\)
さきほど求めた解と違うように見えるかもしれませんが、\(\small y=2(x+3)^2+2\) を展開すると、\(\small y=2x^2+12x+20\) となるので、どちらで求めても同じ解となります。
2つの解法を紹介しましたが、基本的にはどちらも使えるようにしましょう。与えられた放物線の方程式が平方完成した形だった場合、別解の方が楽に解けると思います。与えられた放物線の方程式が平方完成しづらい式の場合、公式を利用した方が圧倒的に楽に求まります。
ちなみに、今回紹介した平行移動の公式は、これから習うすべてのグラフで利用できるので、ここでしっかりと使いこなしておきましょう。
対称移動
続いては対称移動を見ていきます。対称移動には、「線対称移動」と「点対称移動」がありましたね。
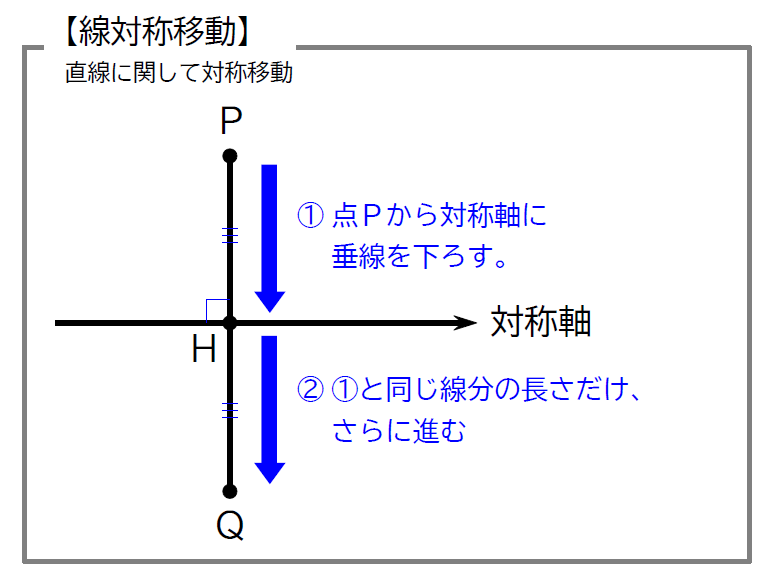
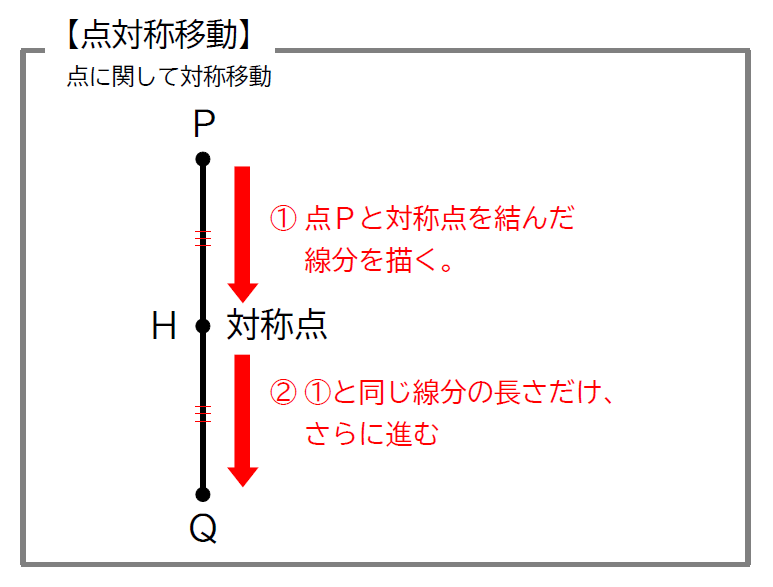
座標平面で、点\(\small \,(5,\ 4)\, \)を\(\small \,x\, \)軸、\(\small \, y\, \)軸、原点に関して対称移動してみます。
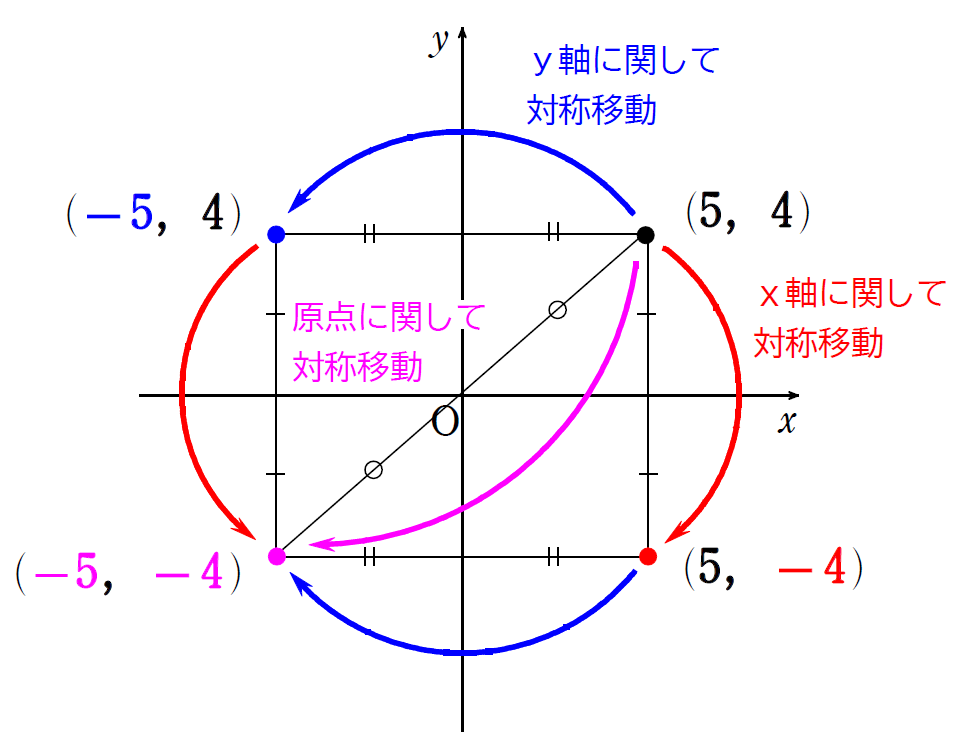
では、放物線を\(\small \,x\, \)軸、\(\small \, y\, \)軸、原点に関して対称移動すると、どうなるか見ていきたいと思います。
放物線上の点\(\small \,(x,\ y )\,\)は、\(\small x\,\)軸に関して対称移動すると、\(\small (x,\ -y)\) となります。この点が満たす関係式は、\(\small -y=f(x)\) となり、これが\(\small \,x\,\)軸に関して対称移動した放物線の方程式となります。
同様に、\(\small y\,\)軸に関して対称移動した放物線の方程式は \(\small y=f(-x)\)、\(\small x\,\)軸に関して対称移動した放物線は \(\small -y=f(-x)\) となります。
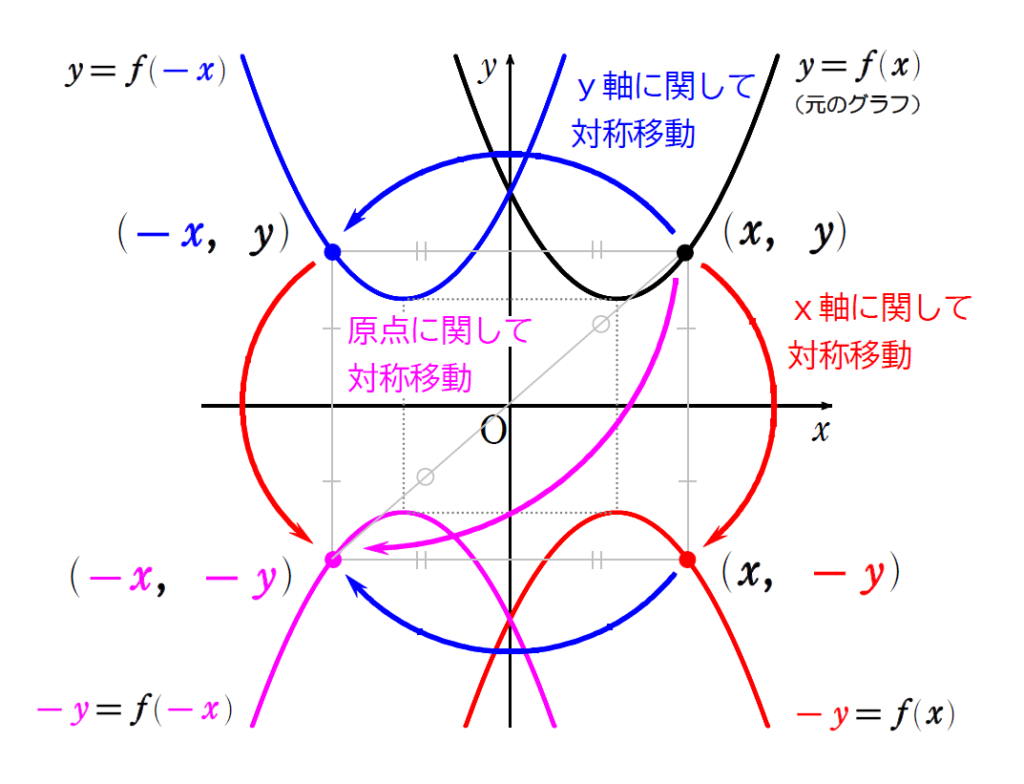
放物線 \(\small y=f(x)\) を
\(\small(1) x\, \)軸に関して対称移動した放物線の方程式は \(\small -y=f(x)\)
\(\small(2) y\, \)軸に関して対称移動した放物線の方程式は \(\small y=f(-x)\)
\(\small(3)\,\,\,\,\)原点に関して対称移動した放物線の方程式は \(\small -y=f(-x)\)
要するに、
\(\small x\, \)軸に関して対称移動するとき
→ \(\small y\,\)を\(\small \, -y\, \)に変える。
\(\small y\, \)軸に関して対称移動するとき
→ \(\small x\,\)を\(\small \, -x\, \)に変える。
原点に関して対称移動するとき
→ \(\small x\,\)を\(\small \, -x\, \)に、\(\small y\,\)を\(\small \, -y\, \)に変える。
ただ、上の公式は丸暗記するのではなく、きちんとグラフをイメージして自分で公式を作れるようにしましょう。
また、頂点を利用して平行移動後の放物線の方程式を求める方法もありますが、上の公式(ポイント)であれば2次関数以外でも使えます。頂点を利用する解法はあまり活躍の場がないので、ここでは触れないで進めてしまいます。
では、公式の使い方を具体的な問題で見てみましょう。
放物線 \(\small y=2x^2+4x+1\) を
\(\small (1) x \, \)軸に関して対称移動した放物線の方程式を求めよ。
\(\small (2) y \, \)軸に関して対称移動した放物線の方程式を求めよ。
\(\small (3)\,\,\,\,\)原点に関して対称移動した放物線の方程式を求めよ。
\(\small (1) y \, \)を\(\small \, -y \, \)に変えれば良いので、
\(\small \begin{align} &-y=2x^2+4x+1\\ \Leftrightarrow \ &y=-2x^2-4x-1\end{align}\)
\(\small (2) x \, \)を\(\small \, -x \, \)に変えれば良いので、
\(\small \begin{align} y&=2(-x)^2+4(-x)+1\\ &=2x^2-4x+1\end{align}\)
\(\small (3) x \, \)を\(\small \, -x \)、\(\small y \, \)を\(\small \, -y \, \)に変えれば良いので、
\(\small \begin{align} &-y=2(-x)^2+4(-x)+1\\ \Leftrightarrow \ &y=-2x^2+4x-1\end{align}\)
式の決定!
条件を満たす放物線の方程式を求める問題を扱っていきます。最初に求める放物線の方程式を文字で表すこととなりますが、式をどう表すかがポイントとなります。
2次関数は以下の3通りの表し方がある。
\(\small (1) y=a(x-p)^2+q\) (標準形)
\(\small (2) y=ax^2+bx+c\) (一般形)
\(\small (3) y=a(x-\alpha)(x-\beta)\) (因数分解形)
使い分けは、
① 頂点・軸に関する条件が与えられているとき、
→ \( \color{magenta}{y=a(x-p)^2+q}\) (標準形)
② \(\small 3\,\)点を通る問題のとき、
→ \( \color{blue}{y=ax^2+bx+c}\) (一般形)
③ \(\small x\,\)軸との共有点に関する条件が与えられているとき、
→ \( \color{#00c800}{y=a(x-\alpha)(x-\beta)}\) (因数分解形)
①~③に当てはまらない場合は、比較的②を使うことが多いです。では、実際の問題で見てみましょう。
次の放物線の方程式を求めよ。
\(\small (1)\) 頂点の座標が \(\small (-1,\ 3)\) で、点 \(\small (1,\ -5)\) を通る放物線。
\(\small (2)\) 軸の方程式が \(\small x=2\) で、\(\small 2\,\)点 \(\small (0,\ 7)\), \(\small (3,\ -2)\,\)を通る放物線。
\(\small (3)\) \(\small 3\,\)点 \(\small (1,\ -1)\), \(\small (2,\ -1)\), \(\small (3,\ 1)\,\)を通る放物線。
\(\small (1)\) 頂点の座標が \(\small (-1,\ 3)\) なので、求める放物線の方程式を \(\small y=a(x+1)^2+3\) とおきます。
点 \(\small (1,\ -5)\) を通るので、
(\(\small \ y=a(x+1)^2+3\) に代入!)
\(\small \begin{align}&-5=a(1+1)^2+3\\ \Leftrightarrow \, &-5=4a+3\\ \Leftrightarrow \, &\,a=-2\end{align}\)
(\(\small \ y=a(x+1)^2+3\) にもどしてあげると)
よって、求める放物線の方程式は、
\(\small y=-2(x+1)^2+3\)
\(\small (2)\) 軸の方程式が \(\small x=2\) なので、求める放物線の方程式を \(\small y=a(x-2)^2+q\) とおきます。
\(\small 2\,\)点 \(\small (0,\ 7)\), \(\small (3,\ -2)\,\)を通るので、
(\(\small y=a(x-2)^2+q\) に代入!)
\(\small \begin{cases}7=4a+q\ &\cdots\ ①\\-2=a+q \ &\cdots\ ②\end{cases}\)
①\(\small -\)②より、\(\small 9=3a \Leftrightarrow a=3\)
①に代入して(②でもOK)、\(\small q\,\)を求めると、
\(\small q=-5\)
よって、求める放物線の方程式は、
\(\small y=3(x-2)^2-5\)
\(\small (3)\) (\(\small 3\,\)点を通る問題なので)求める放物線の方程式を \( \small\color{blue}{y=ax^2+bx+c}\) とおきます。
点 \(\small (1,\ -1)\) を通るので、
\(\small a+b+c=-1 \ \cdots \ ①\)
点 \(\small (2,\ -1)\) を通るので、
\(\small 4a+2b+c=-1 \ \cdots \ ②\)
点 \(\small (3,\ 1)\) を通るので、
\(\small 9a+3b+c=1 \ \cdots \ ③\)
②\(\small -\)①より、\(\small 3a+b=0 \ \cdots \ ④\)
③\(\small -\)②より、\(\small 5a+b=2 \ \cdots \ ⑤\)
⑤\(\small -\)④より、\(\small 2a=2 \ \Leftrightarrow \ a=1\)
④に代入して、\(\small b\,\)を求めると、\(\small b=-3\)
\(\small a,\ b\,\)の値を①に代入して、\(\small c\,\)を求めると、
\(\small c=1\)
よって、求める放物線の方程式は、
\(\small y=x^2-3x+1\)
\(\small (3)\,\)で座標を代入した際、\(\small -1=a+b+c\) ではなく、\(\small a+b+c=-1\) のように左辺と右辺を逆に書いたことに気づきましたか?
これは、その後の連立をしやすくするための工夫です。\(\small (2)\,\)でも、この工夫をすると連立しやすくなります。使わなくても良い工夫ですが、ぜひ真似してみてください。
また、\(\small (3)\,\)の3つの式を連立する方法は、大丈夫ですか?
- Step.11文字消した式を2つ作る
放物線の方程式を求める際には、毎回 \(\small c\) を消去した式を2つ作ると良いです。
- Step.2Step.1で作った2式を連立する
2式を連立する際には、中学校のときに習った連立方程式の解き方でOKです。
- Step.3残りの文字を求める
Step.2で求めた2つの値を、最初の3つの式のどれかに代入して、残りの文字を求めます。
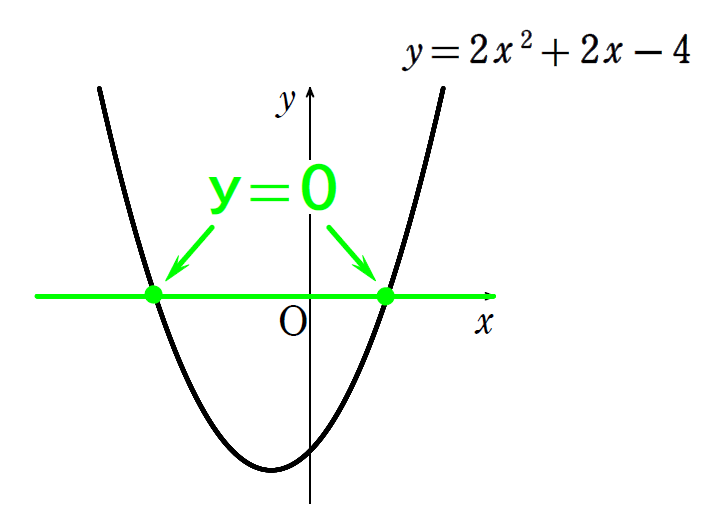
続いては、放物線 \(\small y=2x^2+2x-4\) と\(\small \,x\,\)軸の共有点の\(\small \,x\,\)座標を求めてみましょう。
共有点とは交点のことです。中学校のときにも、直線と\(\small \,x\,\)軸の交点を求めたことがありましたね。
\(\small x\,\)軸上は\(\small \,y\,\)座標が\(\small\,0\,\)です。なので、\(\small y=0\,\)を代入して方程式を解けば、交点の\(\small \,x\,\)座標が求まりました。今回も、同じように求めてみます。
\(\small \begin{align}y=2x^2+2x-4=0 &\Leftrightarrow x^2+x-2=0\\&\Leftrightarrow (x+2)(x-1)=0\\ &\Leftrightarrow x=-2,\ 1 \end{align}\)
よって、\(\small 2\,\)点\(\small \,(-2,\ 0),\ (1,\ 0)\,\)で\(\small \,x\,\)軸と交わることが分かりました。
これと同じ考え方なのが、\( \color{#00c800}{y=a(x-\alpha)(x-\beta)}\)(因数分解形)です。この式で表される放物線は、\(\small \,x\,\)軸と\(\small \,2\,\)点\(\small \,(\alpha,\ 0),\ (\beta,\ 0)\,\)で交わります。逆に、\(\small x\,\)軸との共有点が分かっているとき、その座標から式を求めていくことができるというわけです。
\(\small 3\,\)点 \(\small (0,\ 6)\), \(\small (1,\ 0)\), \(\small (3,\ 0)\,\)を通る放物線の方程式を求めよ。
\(\small 2\,\)点\(\small \,(1,\ \color{#00c800}{0})\), \(\small (3,\ \color{#00c800}{0})\,\)を通るので、
(\(\small \,x\,\)軸と\(\small \,(1,\ \color{#00c800}{0})\), \(\small (3,\ \color{#00c800}{0})\,\)で交わるので、)
求める放物線の方程式は、\(\small \color{#00c800}{y=a(x-1)(x-3)}\) とおけます。
点\(\small \,(0,\ 6)\,\)を通るので、(代入!)
\(\small 6=a\cdot(-1)\cdot(-3) \Leftrightarrow a=2\)
よって、求める放物線の方程式は、\(\small y=2(x-1)(x-3)\)
この問題は、\(\small 3\,\)点を通る問題として、\( \small\color{blue}{y=ax^2+bx+c}\) とおいて解くことも可能ですが、\(\small \color{#00c800}{y=a(x-\alpha)(x-\beta)}\) を利用した方が計算量がダントツで少なくなります。\(\small x\,\)軸との共有点には、なるべく気づけるようにしていきましょう。
また、\(\small y=2(x-1)(x-3)\) は展開しなくても大丈夫という点も抑えておきましょう。
まとめ!
放物線の平行移動、対称移動、式の決定を確認してきましたが、いかがでしたか?
ここまでで、2次関数という単元の3分の1くらいが終わった感じです。
続きの内容は、ここまで説明した内容を理解した上で見ていくこととなります。どれもこれも公式丸暗記としてしまうと、パンクしてしまいます。なによりも対応できない問題がたくさん出てくることにもなります。
仕組みを理解して、分からないところを無くした上で、続きの内容に入っていくようにしていきましょう。





コメント