こんにちは。ねこの数式のnanakoです。
今回は2次関数の最大値・最小値です。関数の意味の復習からしてみましょう。
2つの変数\(\small \,x,\ y\,\)について、\(\small x\,\)の値を定めると、\(\small y\,\)の値が定まるとき、\(\small y\,\)は\(\small \,x\,\)の関数という。
要するに、\(\small x\,\)を代入すると、\(\small y\,\)が求まる関係式です。詳しくは、こちらを確認してください。
2次関数の最大値・最小値
\(\small x\,\)の値をいろいろと変化させたとき、\(\small 2\) 次関数の値が一番大きくなるときと、一番小さくなるときの値を、それぞれ「最大値」「最小値」といいます。
さっそく、問題を見ていきましょう。
次の \(\small 2\) 次関数の最大値・最小値を求めよ。また、そのときの \(\small x\) の値を求めよ。
\(\small(1)\) \(\small y=x^2-2x+4\)
\(\small(2)\) \(\small y=-x^2+4x-3\)
さて、\(\small x\) に何を代入すれば、\(\small y\) が一番大きく(小さく)なるかを調べていきたいわけですが、適当に代入して見つけていくのは難しいですね。
そこで利用するのが、2次関数のグラフです!!
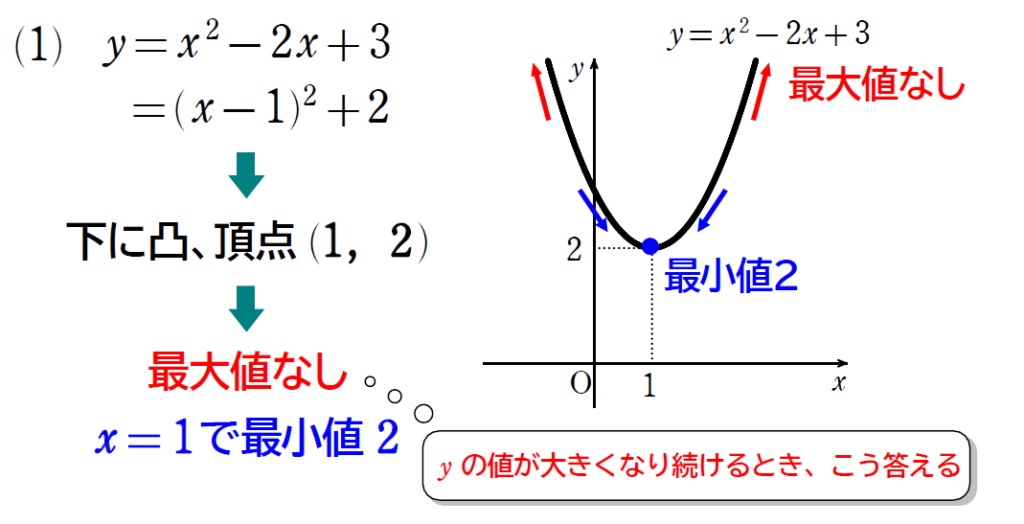
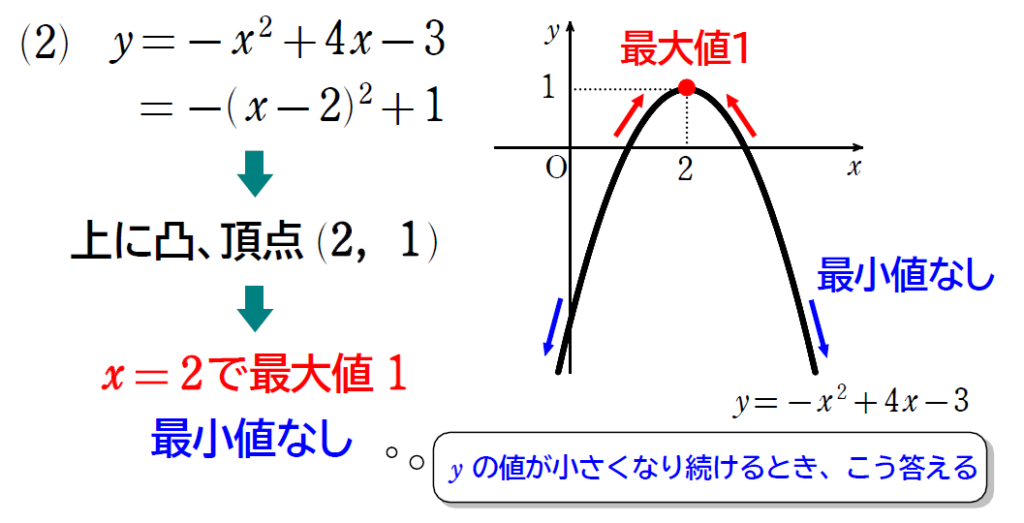
上のような条件の問題を解く際には、グラフは面倒なので書かないことも多いですが、少なくともグラフが頭に浮かぶようにしましょう!
もう一段階レベルを上げてみましょう。
次の \(\small 2\) 次関数の最大値・最小値を求めよ。また、そのときの \(\small x\) の値を求めよ。
\(\small(1)\) \(\small y=x^2-4x+2 (1≦x≦4)\)
\(\small(2)\) \(\small y=-x^2+2x-3 (-1≦x≦2)\)
\(\small(3)\) \(\small y=2x^2+2x+2 (0≦x≦1)\)
\(\small(4)\) \(\small y=-x^2+1 (-1<x<2)\)
最大値・最小値の問題は、増減を利用!
増減を利用・・・、つまり、グラフを利用と考えれば良いです。
先ほどの例題1のように定義域が与えられていない問題では、グラフを省略することも多いですが、今回の問題のように定義域が与えられている問題では、グラフを必ずかきましょう。
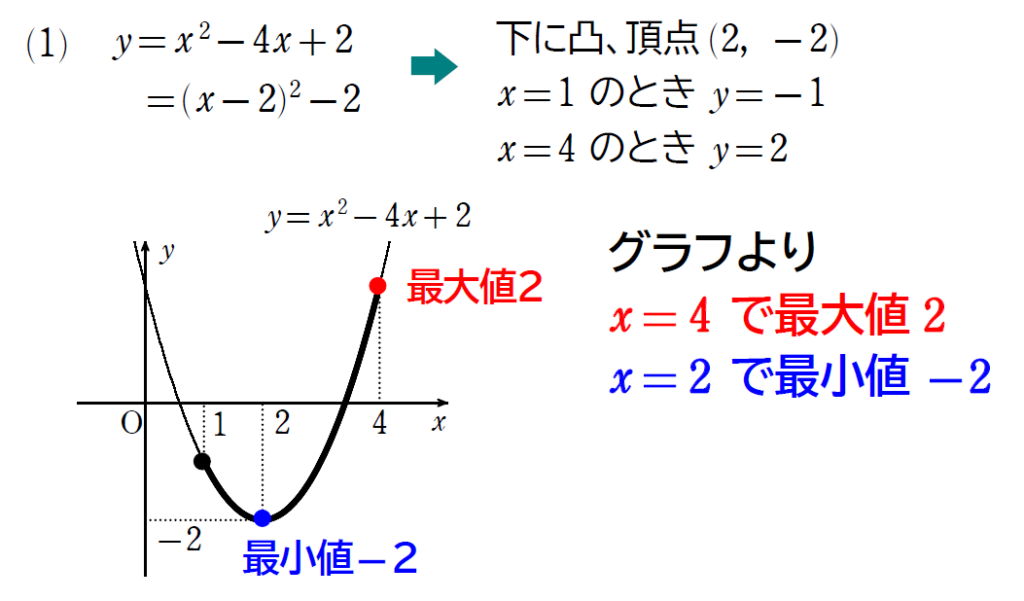
\(\small 1≦x≦4\) をグラフに反映させるのがポイントです。
この解答は丁寧で良いとは思いますが、すべての問題をこのクオリティで解答を書くのは、面倒ですね。
楽をする方法を紹介します。楽をすることだけが目的ではなく、応用問題となったときに活躍する書き方なので、ぜひ真似をしてみましょう。
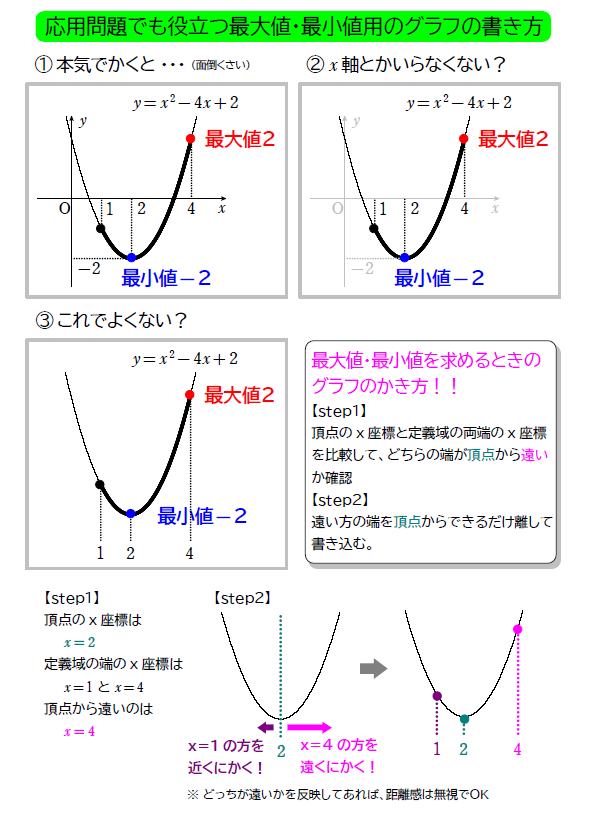
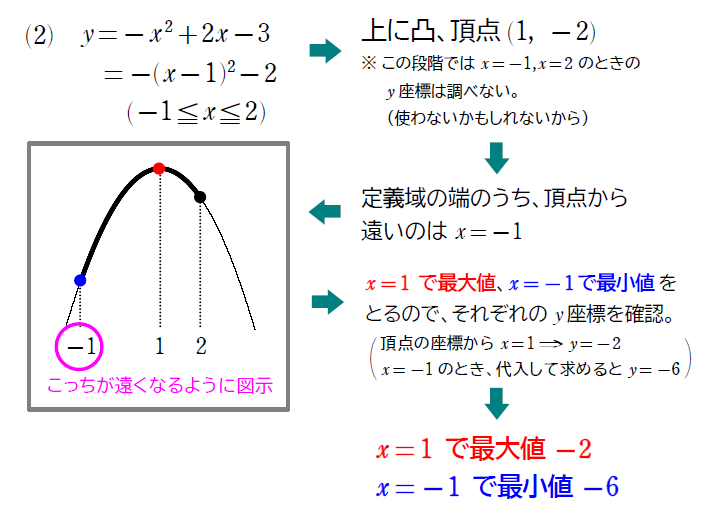
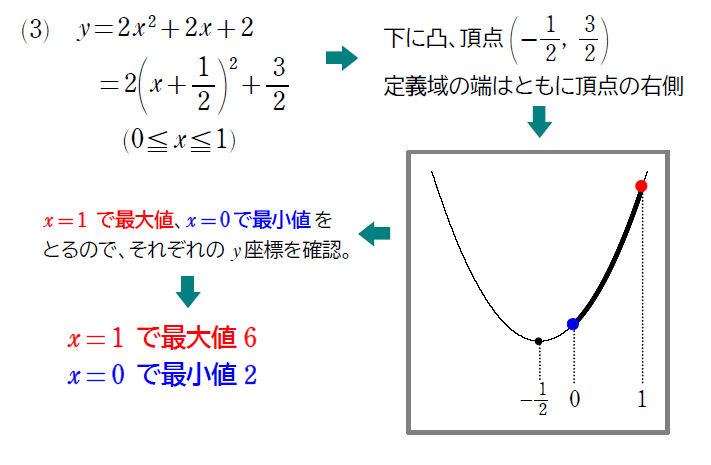
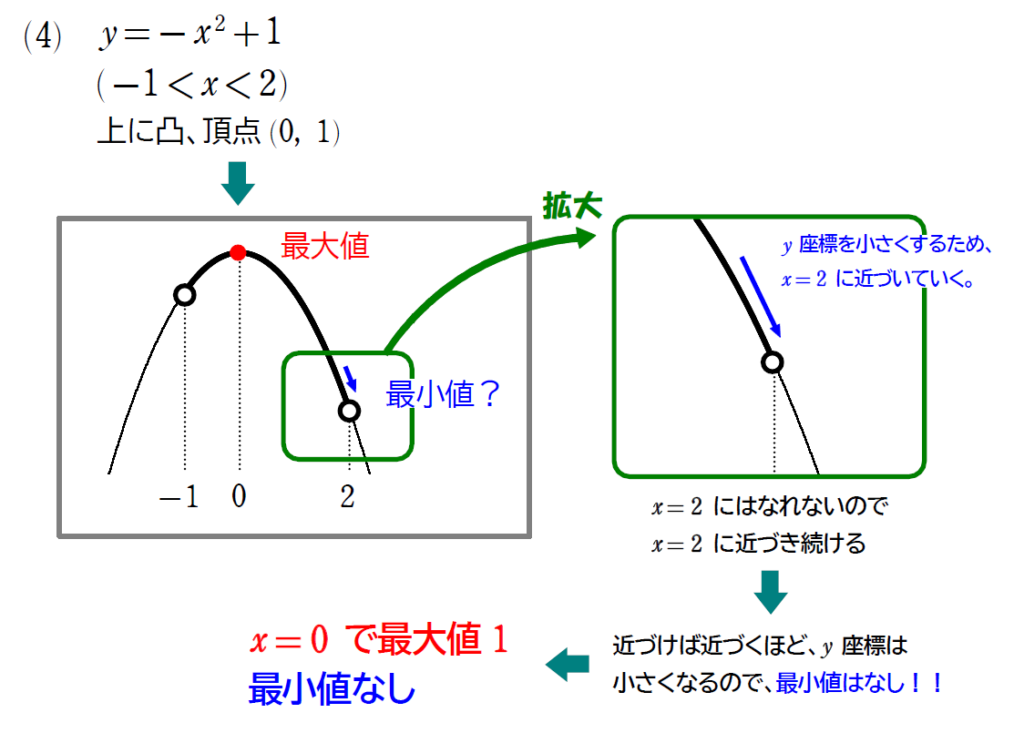
\(\small (4)\) は定義域が \(\small -1<x<2\) となっていて、定義域の端が含まれていません。これによって、最小値がなくなりました。
定義域の端が含まれていないときは、最大値や最小値が「なし」となるので、注意してください。
最大値・最小値の応用問題!
関数の最大値・最小値の応用問題はいろいろな種類の問題があります。系統に分けて説明していきます。
場合分けを利用する最大値・最小値の問題
絶対値でも出てきた場合分けですが、2次関数でも利用します。
数学の世界では何か判断することに困った際に、場合分けをすることで問題を解き進めていきます。

実際の問題でみてみましょう。
\(\small 2\) 次関数 \(\small y=ax^2-2ax+b \ \ (0≦x≦3) \) の最大値が \(\small 5\)、最小値が \(\small -3\) であるとき、定数 \(\small a,\ b\) の値を求めよ。
この問題は最大値・最小値が与えられています。最大値・最小値を求める問題ではないですが、求める問題と同じ流れで進めていきましょう。

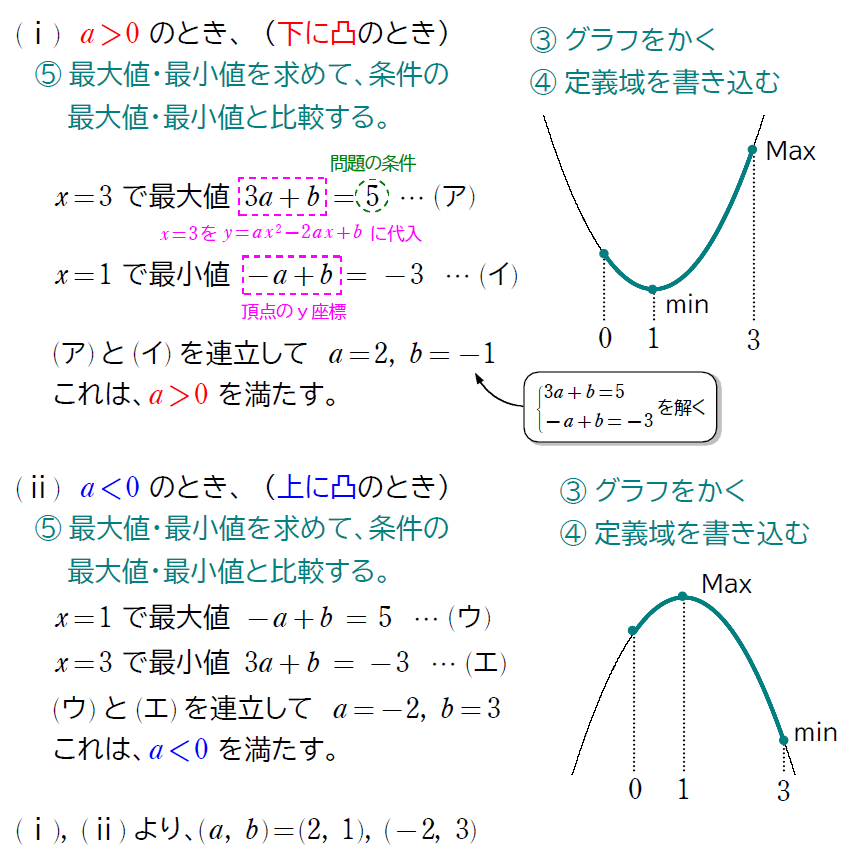
さて、答えは求まりましたが、もう1点注目しておかなければいけない点があるので説明していきたいと思います。「2次関数」という条件です。この言葉は飾りではなく、立派な条件なので注意が必要です。\(\small a=0\) だと、\(\small y=ax^2-2ax+b \) は、\(\small y=b=\)(定数) となり、2次関数とはなりません。つまり、「2次関数」と問題文にあった際には、「\(\small x^2\) の係数が0以外」という条件が発生するので、注意しましょう。
ちなみに、今回の問題で、「2次関数」が、ただの「関数」だった場合は、(ⅰ) \(\small a>0\) と (ⅱ) \(\small a<0\) の場合分けに加えて、(ⅲ) \(\small a=0\) のときの議論もしなければいけません。この場合は、最大値が \(\small 5\)、最小値が \(\small -3\) にはなれないので不適となり、結局は先ほどの例題の解答と同じ答えになってしまいます。必ず不適になるとも限らないので、「2次関数」なのか「関数」なのかを確認し忘れないようにしましょう。
\(\small a\) は正の定数とする。\(\small 2\) 次関数 \(\small y=x^2-4x+5 \ \ (0≦x≦a) \) について、次の問いに答えよ。
\(\small (1)\) 最小値を求めよ。
\(\small (2)\) 最大値を求めよ。
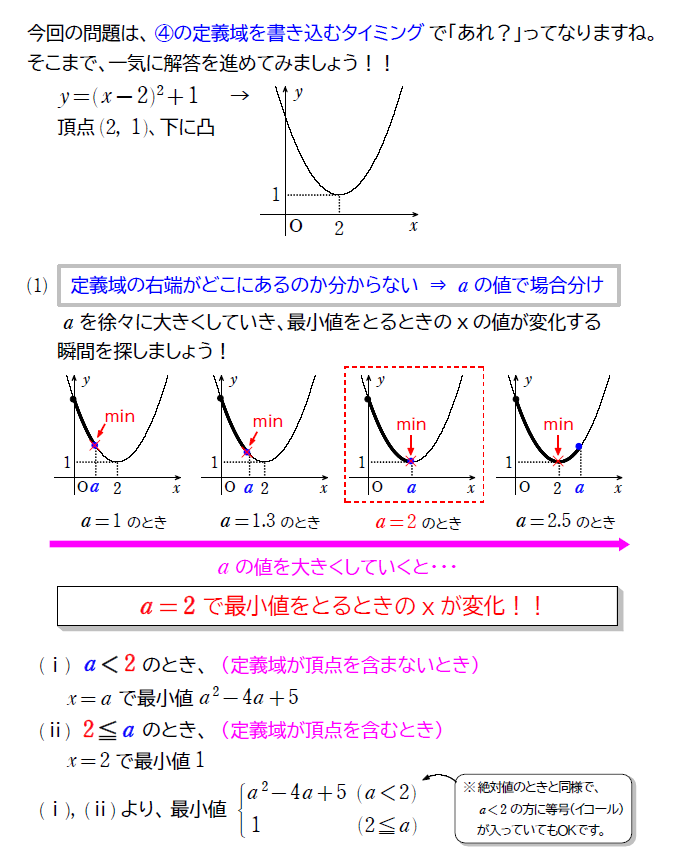
この問題では、グラフを書く際に \(\small x\) 軸や \(\small y \) 軸などは書かないで解いていくこともできますが、慣れていないと解きづらいと思います。上の解答のようにある程度丁寧に書いてあげると良いと思います。
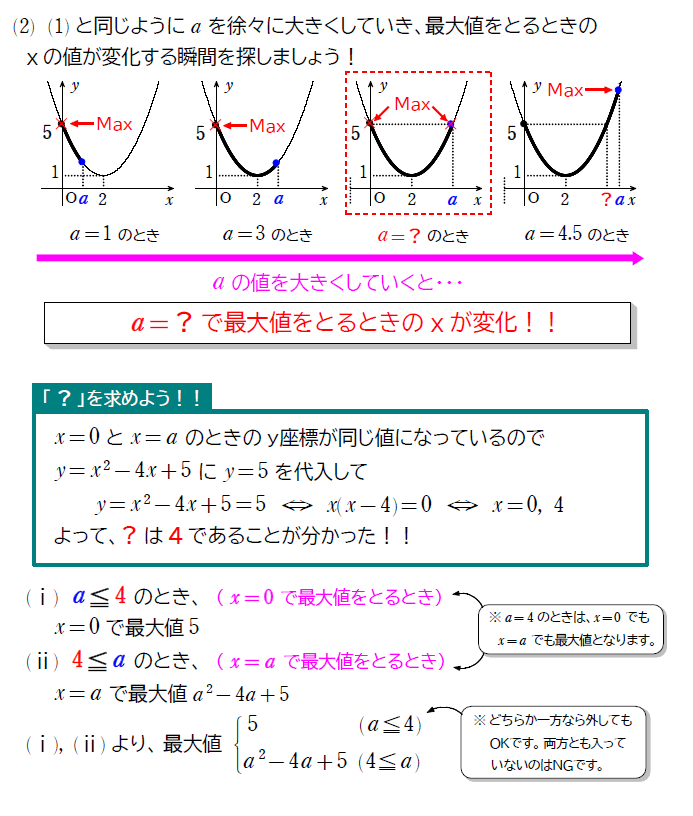
今回の問題は、定義域の右端がヌメヌメと動く様子を想像できると、正確に場合分けができます。今後もこの「ヌメヌメ動かす」ことは多いので、想像できるようにしましょう。
軸の場合分け
通称、軸の場合分け。高1の定期テストの問題で、かなりの難問となる系統です。最大値と最小値で場合分けの仕方が違うので、例題を分けて解説していきたいと思います。
\(\small 2\) 次関数 \(\small f(x)=x^2-4ax+3a^2+1 \ \ (0≦x≦2) \) の最小値を求めよ。
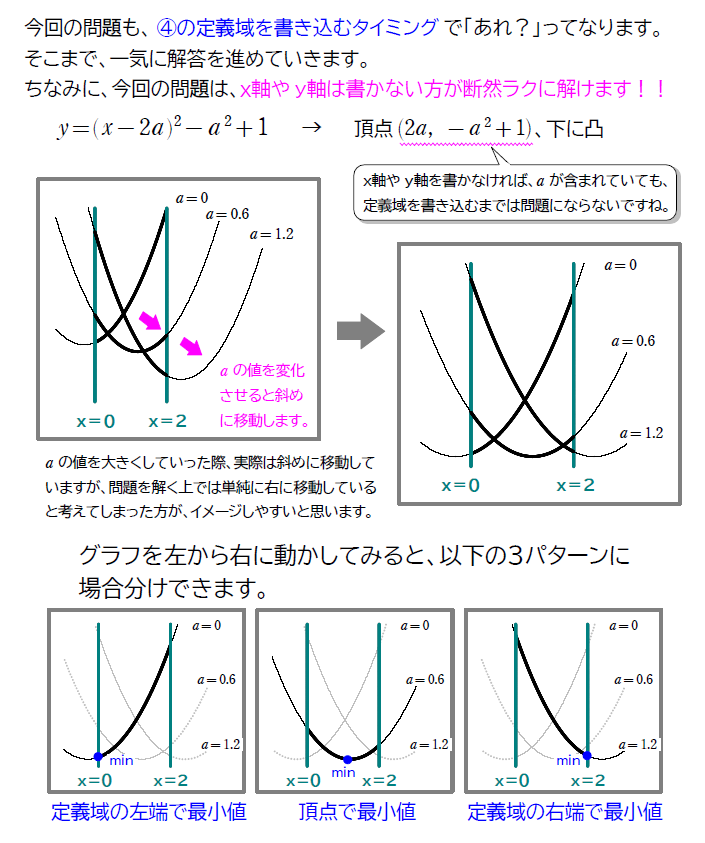
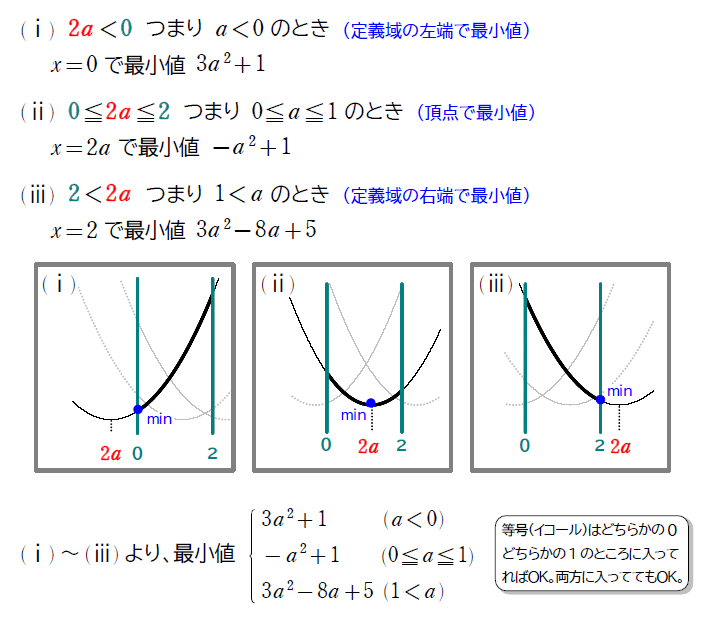
続いては最大値を求めてみましょう。
\(\small 2\) 次関数 \(\small f(x)=x^2-4ax+3a^2+1 \ \ (0≦x≦2) \) の最大値を求めよ。
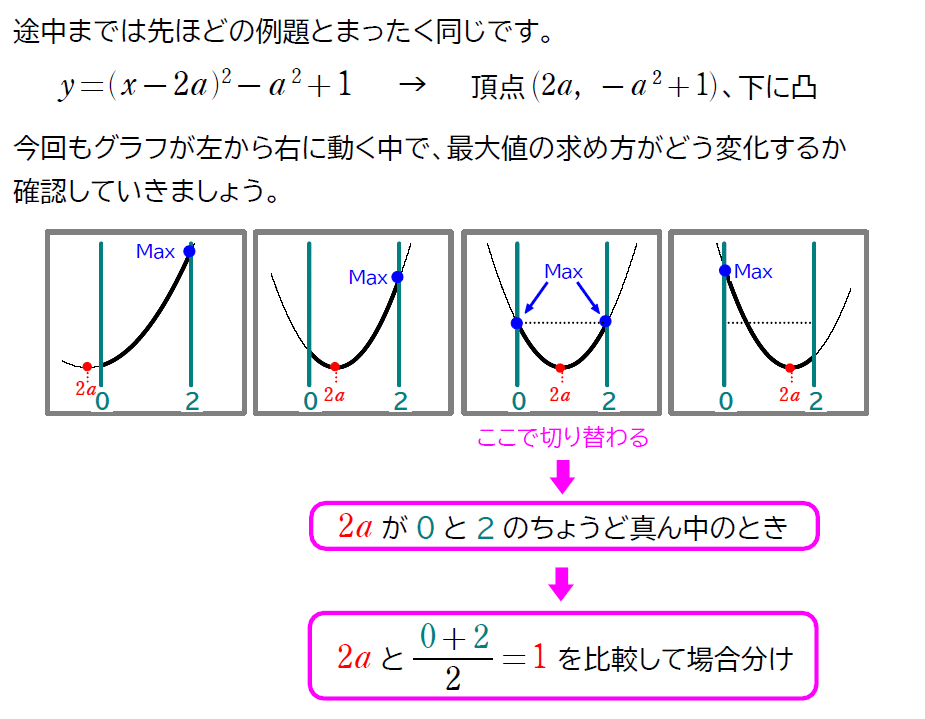
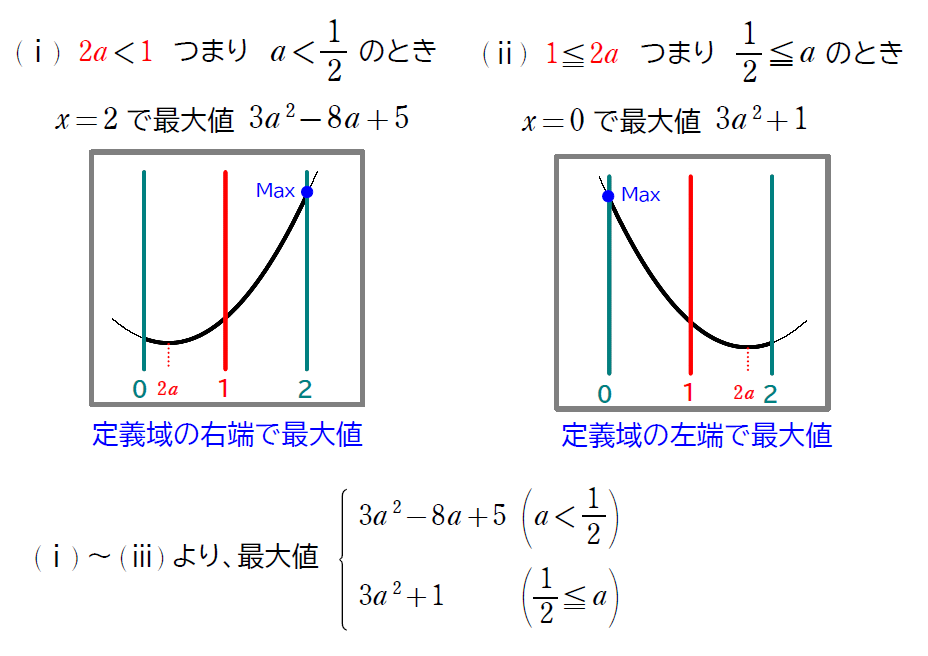
この問題でも、\(\small\displaystyle a<\frac{1}{2}\) と \(\small\displaystyle \frac{1}{2}≦a\) はどちらかに等号が入っていいればOKです。
今回の軸の場合分けの問題では、グラフが下に凸でしたが、上に凸のグラフになると最大値と最小値の場合分けの仕方が入れ変わります。
軸の場合分けは、バリエーションが豊富なので、丸暗記するのではなく、しっかりと理解した上で、他のパターンの問題にも通用するようにしていきましょう。
2変数の最大値・最小値
続いては、変数が2つ含まれている関数の最大値・最小値の問題です。
\(\small x,\ y\) を実数とする。次の問いに答えよ。
\(\small (1)\) \(\small x+y=1\) のとき、\(\small x^2+2y\) の最大値・最小値を求めよ。また、そのときの \(\small x,\ y\) の値を求めよ。
\(\small (2)\) \(\small x≧0,\ y≧0,\ x+2y=4\) のとき、\(\small x+y^2\) の最大値・最小値を求めよ。また、そのときの \(\small x,\ y\) の値を求めよ。
例題6は条件式が与えられたときの2変数の最大値・最小値の問題です。
\(\small (1) \) では、\(\small x+y=1 \) という式が与えられています。この式を満たす \(\small x,\ y \) の組をすべて考えて、\(\small x^2+2y\) の値が最も大きいときと、最も小さいときの値を求めよ…という問題です。

適当な \(\small x,\ y \) の値を代入して最小値を求めてみようよ!

じゃあ、\(\small x\) の値を決めて、\(\small y\) を求めた後に、\(\small x^2+2y\) の値を求めてみましょう。


どの組合せで最小値になるか、求まる気がしない・・・

そうですね。では、代入する値を■にして、同じ計算をしてみましょう。
求め方が見えてきますよ。
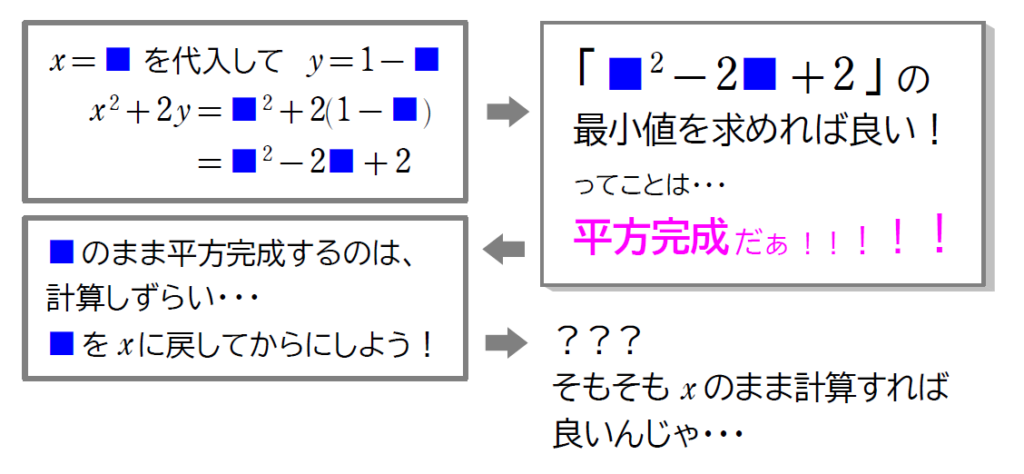
念のため、解説に入る前にもう1点ポイントを抑えておきましょう!

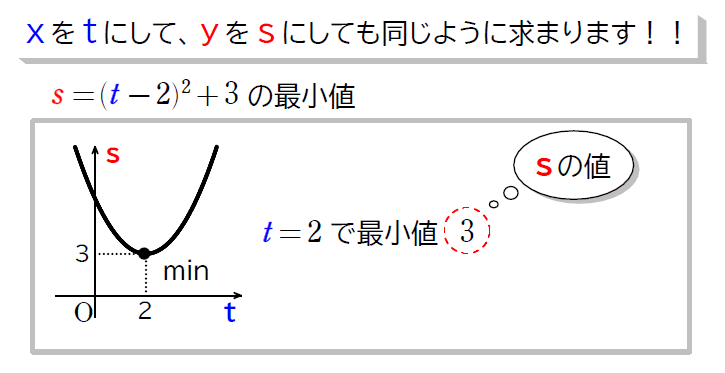
つまり!!
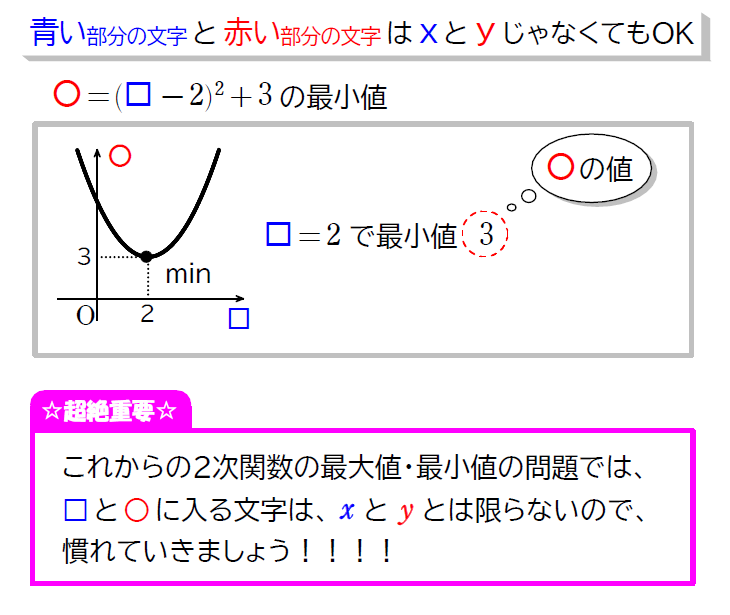

お待たせしました。解説を見ていただきましょう!!
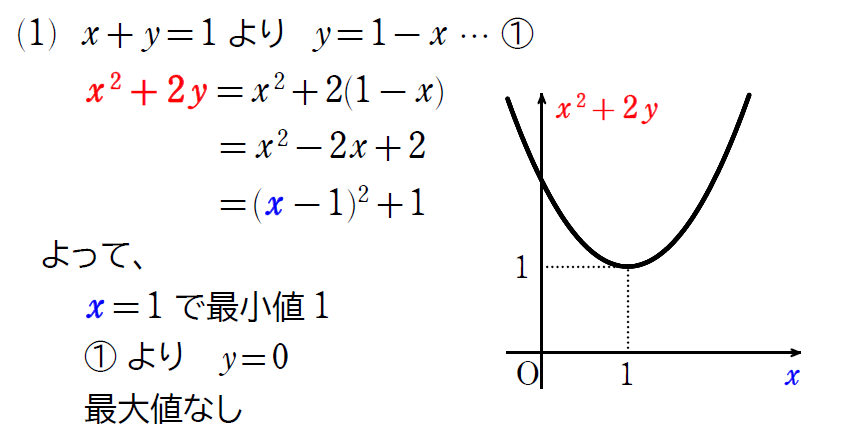
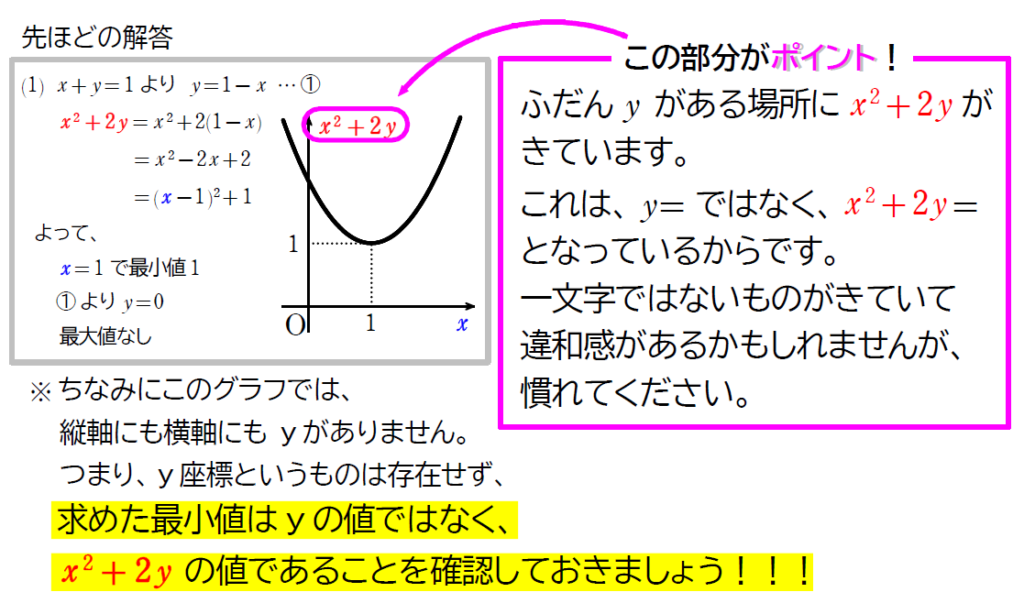
\(\small (2)\) も同じように考えて解いていきますが、さらにポイントが1つ追加されるので気をつけてみていきましょう!
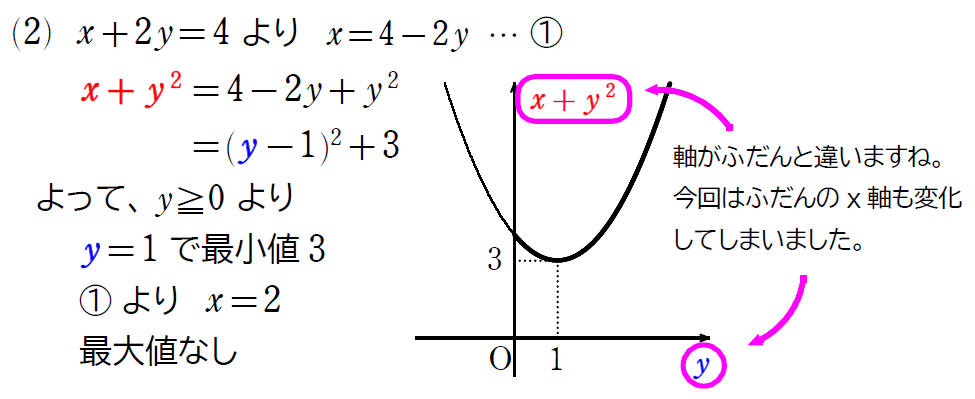
この解答、\(\small (1)\) をふまえて、ちゃんと解けていそうですが、実はトラブルが発生しています。詳しく見ていきましょう。
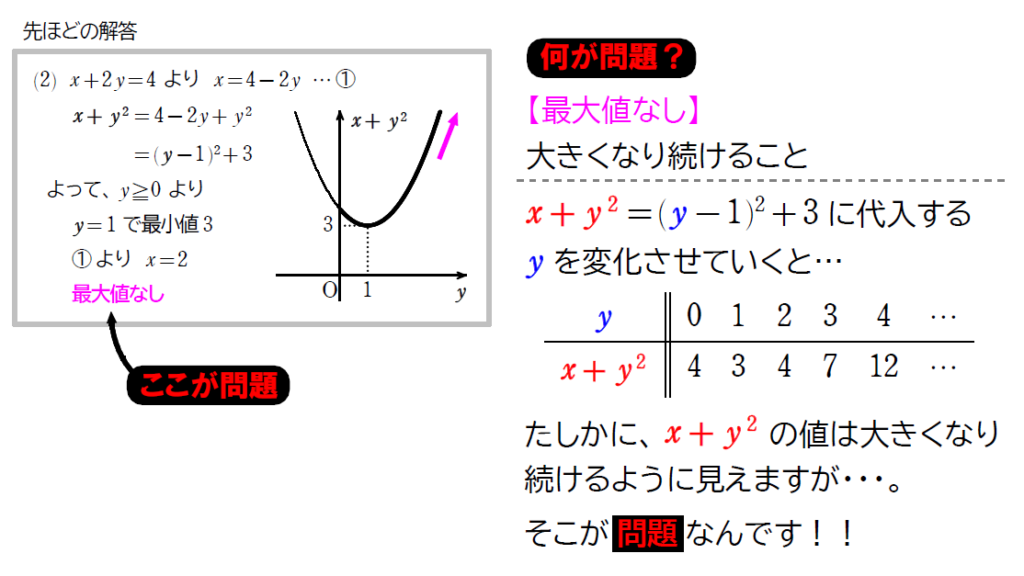

ということで、正しい解答は・・・
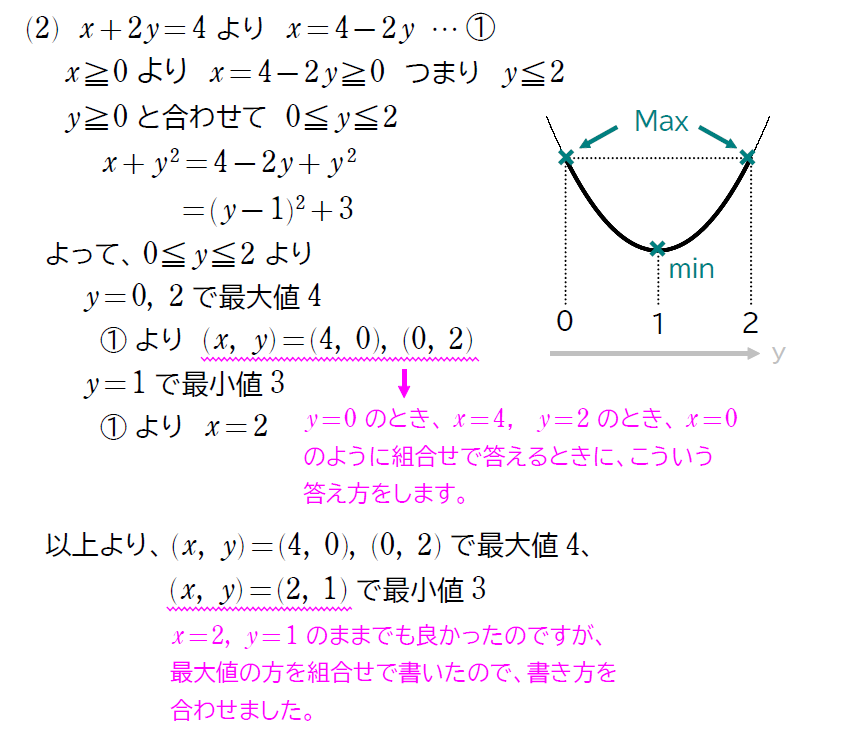
まとめておきましょう!!
条件式があるとき ⇒ 1文字消去!
消去するものに範囲があるとき ⇒ 残される文字に範囲をうつす!
次の『例題6 おかわり!』は2次不等式を利用します。まだ学習していない方は例題7に飛んでください。
\(\small x,\ y\) を実数とする。\(\small x^2+y^2=1\) のとき、\(\small x^2+4y\) の最大値・最小値を求めよ。また、そのときの \(\small x,\ y\) の値を求めよ。
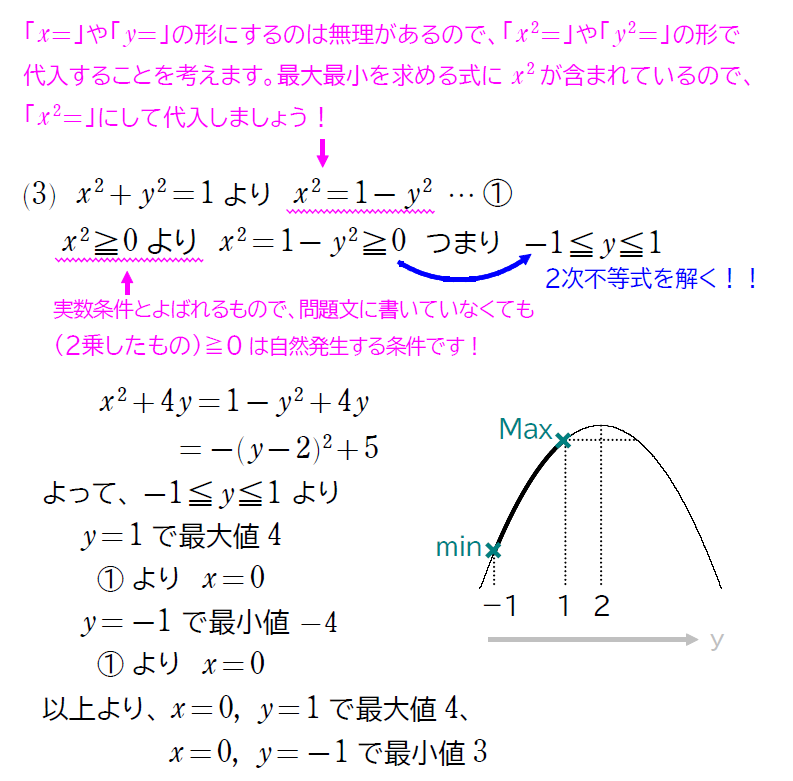
続いても、2変数の最大値・最小値の問題です。
\(\small x,\ y\) を実数とする。関数 \(\small x^2+2xy+3y^2+4x+8y+9\) の最小値を求めよ。また、そのときの \(\small x,\ y\) の値を求めよ。
今回の問題は条件式を利用して、1文字消去することができないので、がっつり2変数で最小値を求めていきましょう。
ここで、数学を学ぶ上で重要な考え方 を紹介します。
私たちは、数学の世界でも実生活でも、2つ以上同時に変化するものへ対応することは難しいです。例えば、2匹ハエが飛んでいるとき、2匹のハエを同時に見続けることは無理ですよね。
なので、数学の世界では2つ以上同時に変化するものがあるとき、固定 という考え方を利用します。
2つ以上同時に変化するものがあるとき ⇒ 固定!
実際の問題を通して、紹介していきましょう。
今回の問題では \(\small x,\ y \) の2変数(文字)が変化します。なので、1文字固定します。
具体的に固定とは、変化させない=定数として考える ことをさします。
\(\small y \) を固定して(定数と考え) \(\small x \) の2次関数の最小値の問題としてみてみましょう。\(\small x\) に注目して式を整理して平方完成しましょう。文字がたくさんあるときの因数分解の問題と同じ対応です。

次の関数 \(\small y=(x^2-2x+2)^2+4(x^2-2x-2)+7\) 最小値を求めよ。また、そのときの \(\small x\) の値を求めよ。

え?このまま最小値を求めようとすると、4次関数を考えることになっちゃうよ!

そうですね。4次関数の最小値は、数Ⅱの微分法を利用することになります。

習ってない・・・

実は工夫をすることで、2次関数の最大値・最小値の問題として解くことが可能なんです!

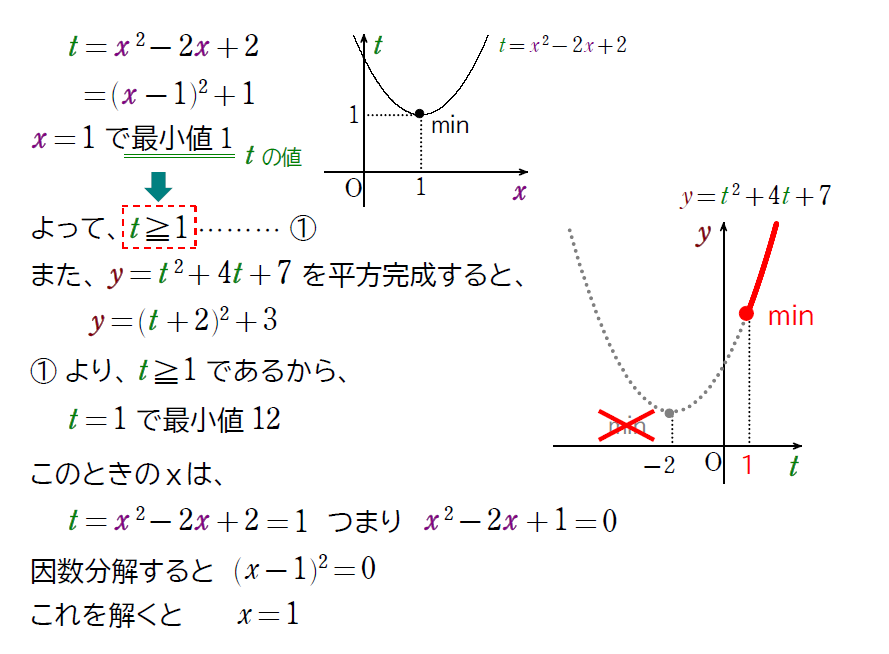
まとめ!
2次関数の最大値・最小値はまだまだいろんなパターンがあります。どのパターンも今回紹介した内容を応用していくような流れになるので、仕組みも含めてしっかりと復習しておきましょう!!






コメント