こんにちは。ねこの数式のnanakoです。
高校数学でなが~くお世話になる三角比の登場です!
サイン、コサイン、タンジェント、物理などですでにご存じの人もいるかもしれませんが、一から丁寧に説明していきます!
本編に入る前に、三角比の歴史を紹介!!(聞けない環境の人はスルーで問題ないですw)

直角三角形と三角比の定義
さて、長さを計るために開発された三角比を紹介する前に、こんな問題を見てみましょう。

あの山の高さを調べてみましょう。どうしましょうか?(というか、どこの山なんでしょ?)
正面から見た図だと説明しづらいので、横から見た形で説明していきましょう。
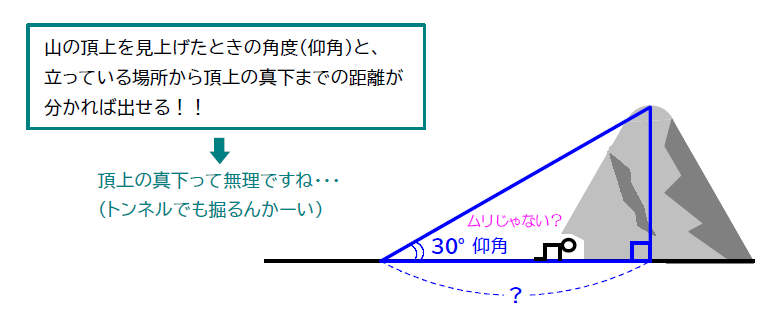
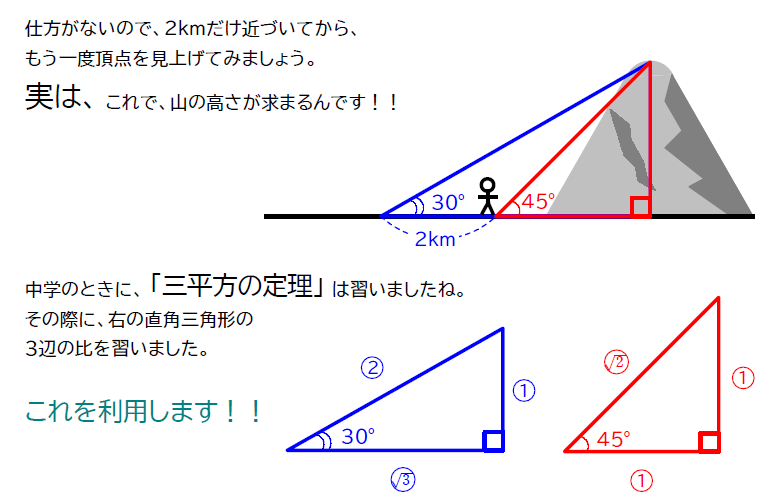

これを応用して、昔の人は地球の半径や月までの距離を調べたりしたんですよ。
ではでは、最初に見上げた際の角度(仰角)が\(\small \,10^\circ\,\)だったら、どうします?
\(\small \,30^\circ\,\)になるまで近づくのも一つの方法ですが、もっと簡単な方法があります。

定規、鉛筆、分度器、紙、これだけで解消します!
これらの道具を利用して、1つの角が\(\small \,10^\circ\,\)の直角三角形を書いて、辺の比を求めてみましょう!!
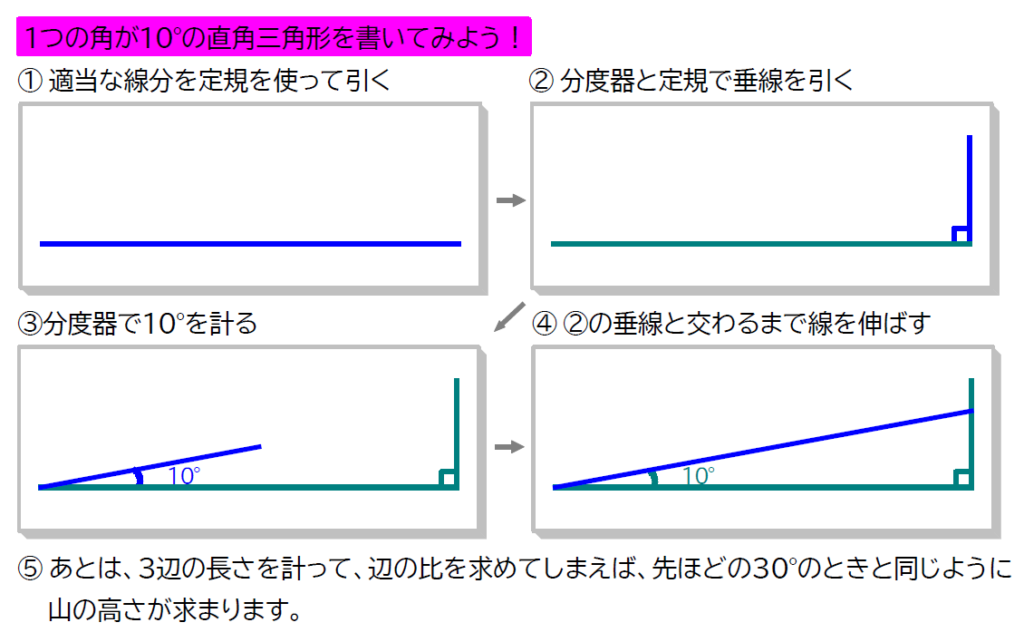

ちなみに、先ほど求めた \(\small \tan10^\circ ,\,\sin10^\circ,\,\cos10^\circ \) は、直角三角形が正確には書けていなかったので、値も正確ではありません。正確な値は、
\(\small \sin10^\circ=0.173648178\)
\(\small \cos10^\circ=0.984807753\)
\(\small \cos10^\circ=0.176326981 \)
ただし、これらの値は無理数なので、\(\small \sqrt{2}\) みたいに永遠と続く数字です。
(そういう意味では正確とは言えませんね・・・笑)
では、ようやく『三角比の定義』(どう決めるか)を見ていきましょう!!
三角比の定義ってナニ?
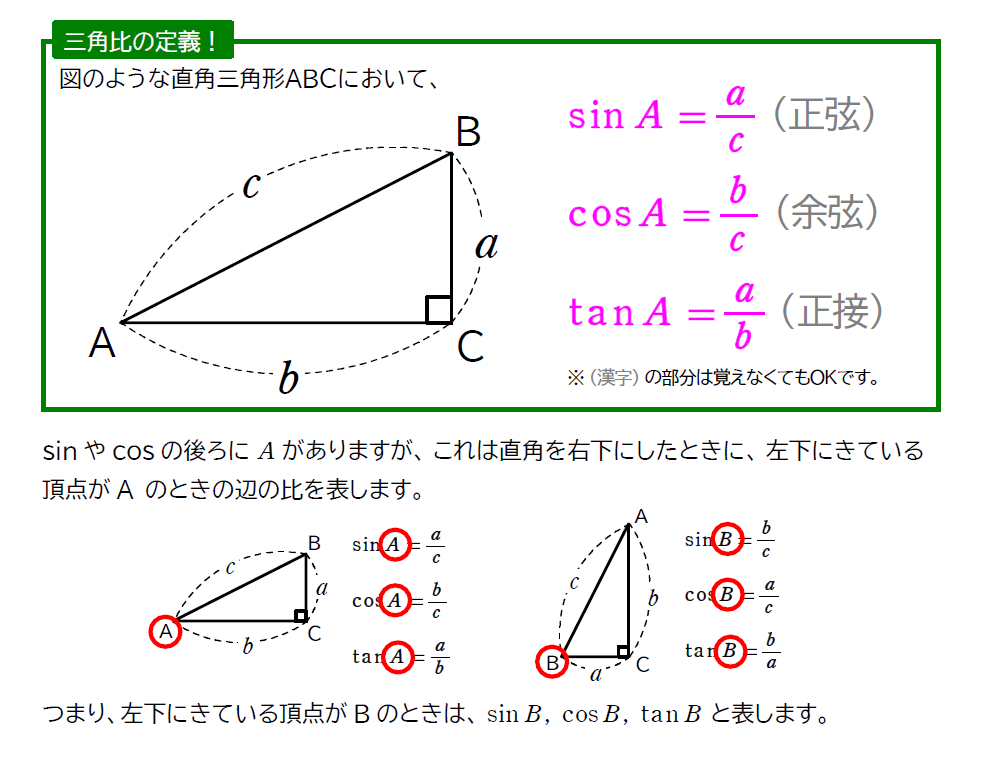

では、問題を通して求め方を確認してみましょう!
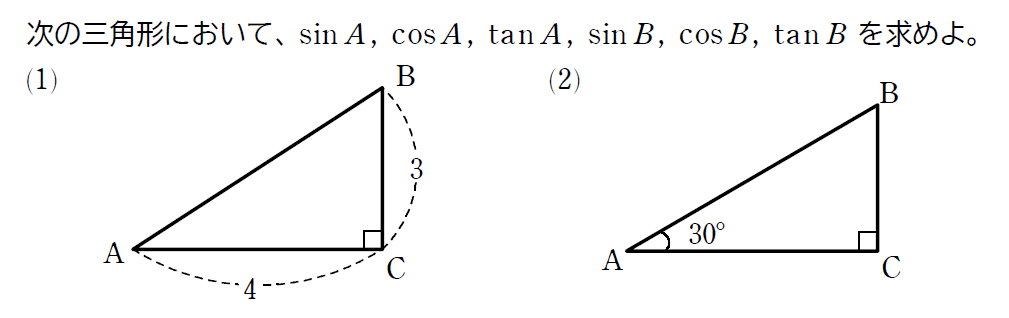
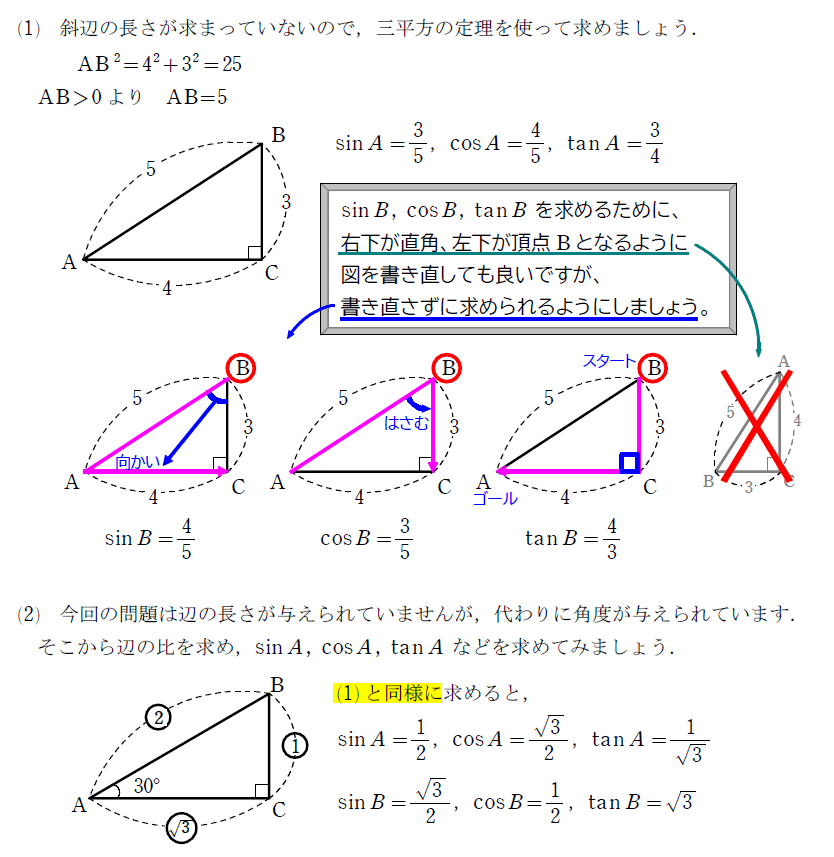

今回の例題の(2)では \(\small \angle \)A\(\small =30^\circ\) でした。このとき、\(\small \sin A\) は \(\small \sin30^\circ\) と表します。(もちろん \(\small \sin A\) と表しても問題ありません。) つまり、\(\small \sin A\) の \(\small A\) は、頂点 A という意味ではなく、頂点 A の角度という意味だったのです。そして、角度が \(\small 30^\circ,\ 45^\circ,\ 60^\circ \) の三角比は、今後よく使うので覚える必要があるのですが、このタイミングでは覚える必要が無いので、その時がきたら、お知らせします。
あと、もう1点お伝えすることがあります。辺の長さや面積などは有理化すると教わってきましたが、三角比の値は有理化しなくて良いです。2辺の比を分数で表したものなので、有理化しない方が分かりやすい場合もあるからです。まぁ、有理化するかどうか迷ったら有理化しておきましょう。
三角比の相互関係ってナニ?
相互関係というのは、お互いの関係って意味です。\(\small \sin\) と \(\small \cos\) と \(\small \tan \) の関係を求めよう!って話です。三角形だけに、三角関係だったり!・・・
あい、なんでもないです・・・
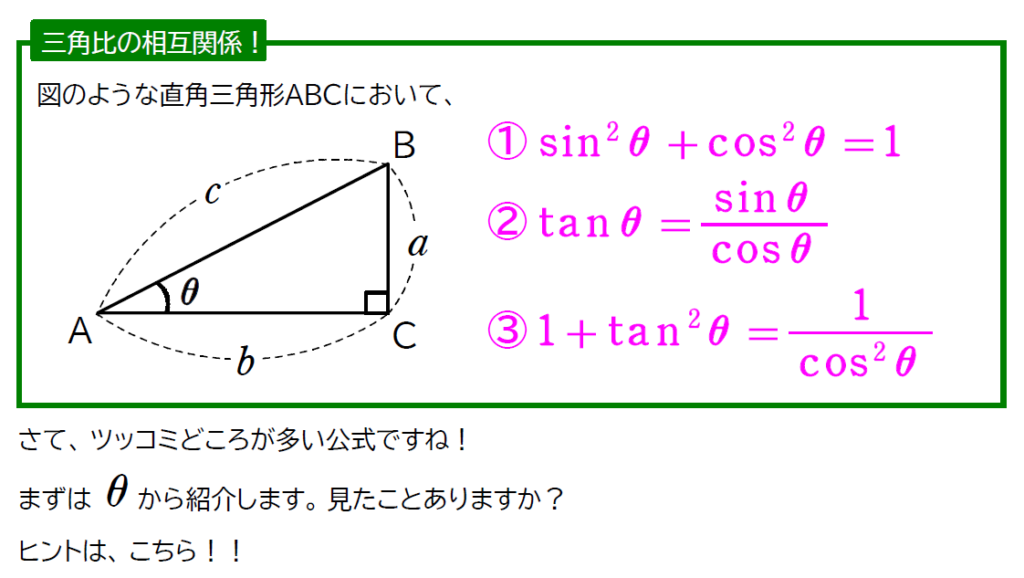



三角比の相互関係の公式の証明を下に載せておきます。公式の①と②の証明はさておき、③の証明は覚えておいた方が、公式を覚える上でも良いかと思います。



\(\small 0^\circ< \theta <90^\circ\) とする。\(\small \sin \theta =\displaystyle \frac{1}{3}\) のとき、\(\small \cos \theta,\ \, \tan \theta \) を求めよ。


三角比の拡張と単位円
続いては、三角比の拡張です!
突然ですが、\(\huge \color{red}{\sin120^\circ} \)が必要なんですが、どうしたら良いですか?
なぜ必要になってしまったのかはさておき・・・無理じゃない? (´・ω・`)
って、思いますよねー。実際、無理ですもんね~。
直角三角形の1つの角を \(\small 120^\circ \) にしようとすると、三角形が爆発しますもんね。(内角の和が\(\small \, 180^\circ \, \)超えます)
ということで、昔の人は思いっ切った決断を!!
「これまでの話は無かった事にしよっか?」と・・・
は?
いや、だから \(\small \sin120^\circ\) が求まらないから、新たに定義し直すことにしましたとさ。
(これまでの話はなんだったんだか・・・)
三角比の拡張ってナニ?
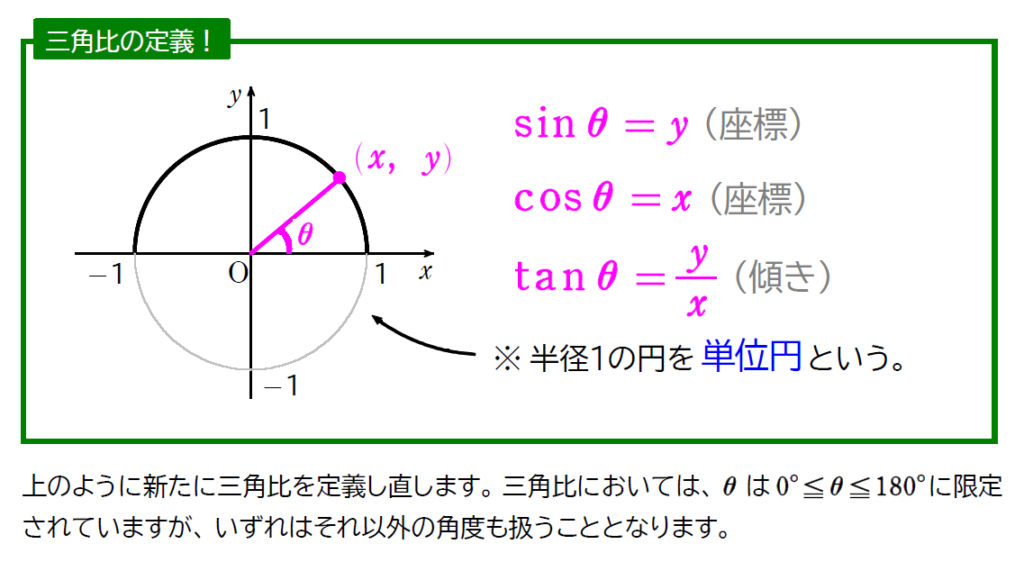

さて、実際に定義を使って \(\small \sin 120^\circ\) の値を求めてみたいと思います。今回は、文字だけだと理解しづらいかもしれないので、動画を用意しました。動画が見れる環境の人は動画を、そうじゃない人は、下の説明を確認してみてください。
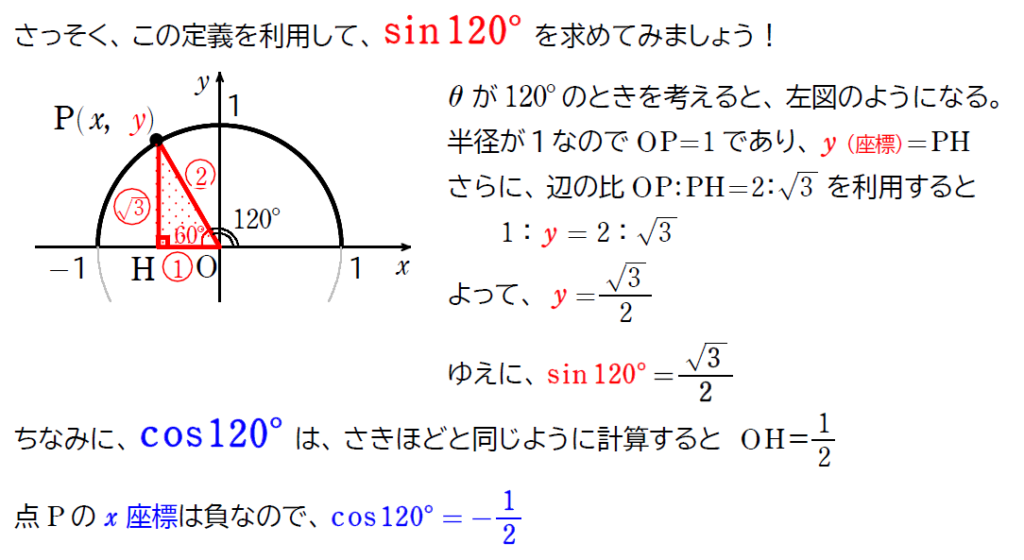
これらの三角比の値は頻繁に利用します。そのため、角度が \(\small 0^\circ ,\ 30^\circ ,\ 45^\circ , \ 60^\circ,\ \ 90^\circ,\ \ 120^\circ,\ \ 135^\circ,\ \ 150^\circ,\ \ 180^\circ \) のときの \(\small \sin ,\ \cos ,\ \tan \) の値はすべて覚えないといけません。
下の表の値を覚えて、九九のように瞬時に答えられるようにしていきます!!!
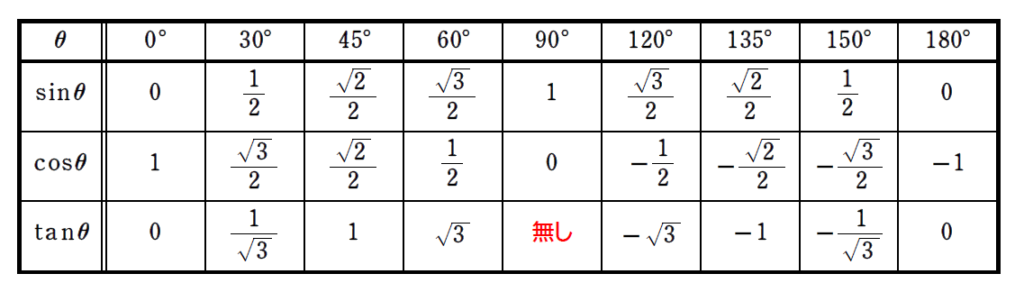
お、お、おぼえられるかー!!!
ということで、三角比の覚え方の動画も用意したので参考にしてください。かなり重要な内容となるのでテキトーに流さないようにしましょう。この単元の最大のポイントですからね!!
上の動画で紹介した。練習用動画です。
動画内でも言っていますが、何度も見ながら練習して、次からの内容に備えていきましょう!
帰ってきた相互関係ってナニ?
帰ってきたウルトラマン的な立ち位置(?)なのが、次の公式です。
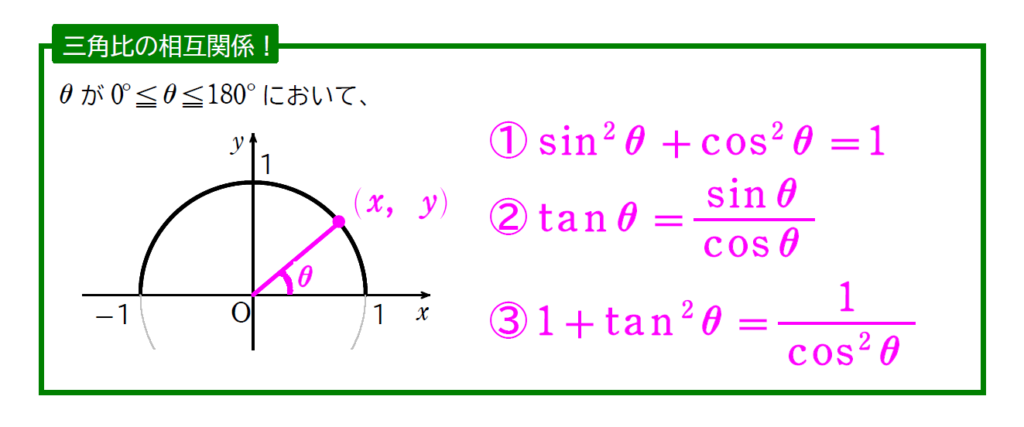
証明はこれまでのものを組み合わせるような形でできます。今回は省略しますね。
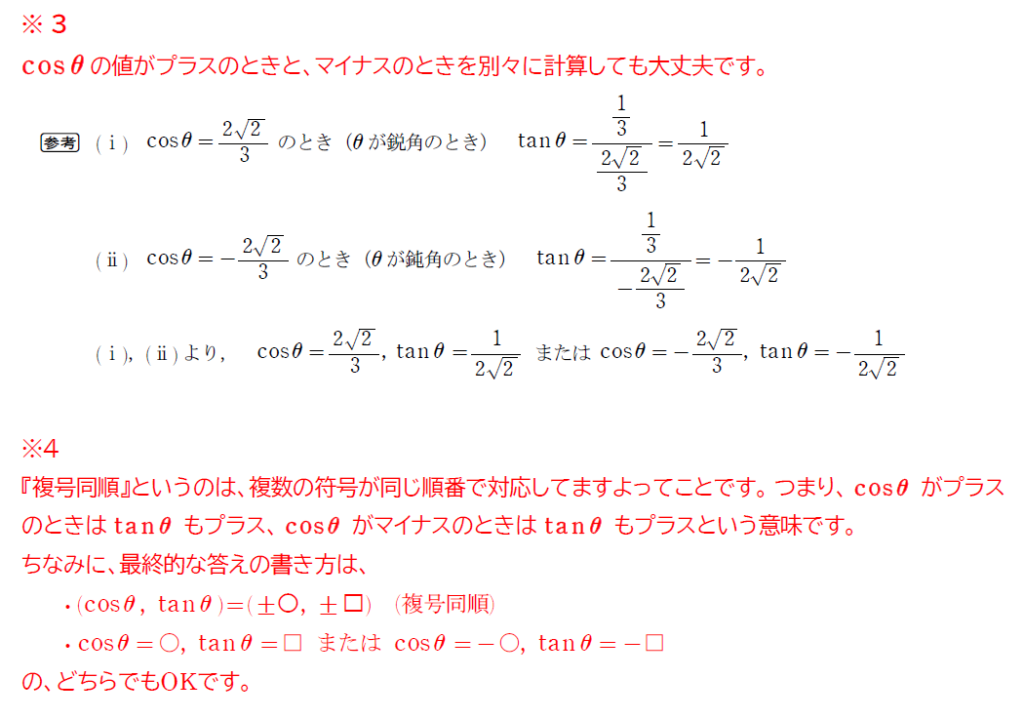
\(\small 0^\circ≦\theta ≦180^\circ\) とする。\(\small \sin \theta =\displaystyle \frac{1}{3}\) のとき、\(\small \cos \theta,\ \, \tan \theta \) を求めよ。
さて、先程の例題2での伏線を回収しましょう。解説も例題2のものと比較しながら見ていきたいと思います。

続いては、三角比+対称式の問題です。対称式の復習は下の記事を参考にしてください。
\(\small 0^\circ≦ \theta ≦180^\circ\) とする。\(\small \sin \theta + \cos \theta =\displaystyle \frac{1}{3}\) のとき、次の値を求めよ。
\(\small (1) \sin \theta \cos \theta\)
\(\small (2) \sin^3 \theta + \cos^3 \theta \)
\(\small (3) \displaystyle \frac{1}{\sin \theta}+\frac{1}{\cos \theta} \)
\(\small (4) \sin \theta \,- \cos \theta \)


90°-θ,180°-θの公式ってナニ?
\(\small \sin150^\circ \) と \(\small \cos30^\circ \) は同じ値ですね。
このように違う三角比でも同じ値となるものがあります。
これらの三角比の関係を公式にしたものを紹介します。

この公式は丸暗記するよりも、自分で作ってしまった方が楽なので、公式の作り方を紹介した動画を用意しました。
さっそくこの公式を使う問題を紹介してみようと思います。
次の三角比を45°以下の三角比で表せ。
\(\small (1) \sin105^\circ \)
\(\small (2) \cos132^\circ \)
\(\small (3) \tan160^\circ \)

まとめ and 確認テスト!
どうでしたか、三角比は?繰り返しになりますが、これ以降の内容は三角比の値を九九のように扱います。数Ⅰ三角比はもちろん、数Ⅱ三角関数(三角比の続き)が得意な単元となるか、不得意な単元となるかは、この三角比の値の覚え方(求め方)がすべてとなるので、動画を何度も繰り返し見て、この後の内容に備えていきましょう。
確認テストはこちらから!
続きや前の内容はこちらから!
他の単元の学習はこちらから







コメント