こんにちは。ねこの数式のnanakoです。
今回の目玉はなんと言っても「解の配置」です。2次関数の応用問題の中でも、沼のように底なしに難易度を上げられます。(笑)
他にもいろいろと2次関数の応用問題を紹介していきます。「解の配置」も含めて、ちゃんと仕組みが理解できれば、解けるようになるので、あきらめずに頑張りましょう。
平行移動・対称移動・式の決定
これらの内容を踏まえた問題を見ていきます。
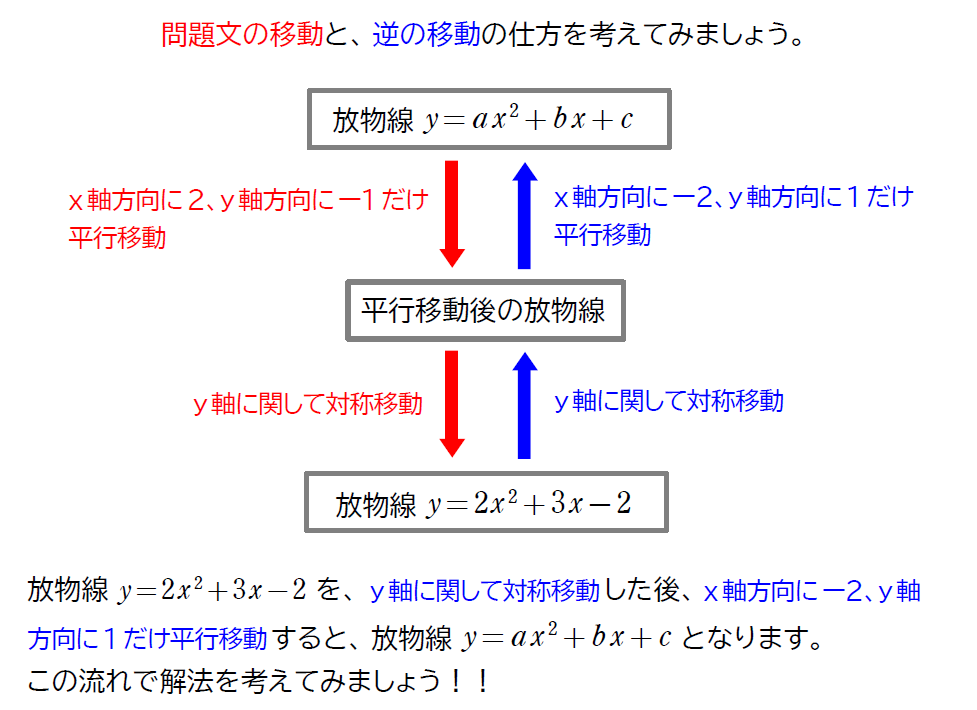
放物線 \(\small y=ax^2+bx+c\) を\(\small \,x\,\)軸方向に\(\small \,2\)、\(\small \,y\,\)軸方向に\(\small \,-1\,\)だけ平行移動した後、\(\small y\,\)軸に関して対称移動したものの方程式が、\(\small y=2x^2+3x-2\,\)となった。このとき、定数\(\small \,a,\,b,\,c\,\)の値を求めよ。
この問題は、難しいわけではないのですが、知らないと損をするような問題です。


放物線\(\small \, y=-x^2+3x\,\)を平行移動したもののうち、点\(\small \,(1,\,1)\,\)を通り、頂点が直線\(\small \, y=2x-1 \,\)上にある放物線の方程式を求めよ。

最大値・最小値
今回も下の記事を踏まえた内容です!
特に、「軸の場合分け」を確認した上で見ていきましょう。
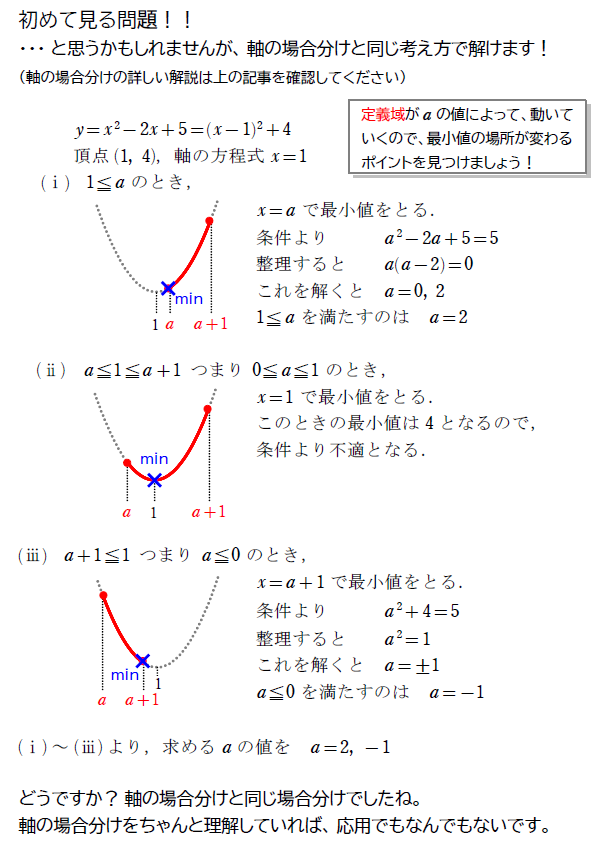
2次関数\(\small \, y=x^2-2x+5\ \ (a≦x≦a+1) \,\)の最小値が \(\small 5 \) となるような定数 \(\small a \) の値を求めよ。
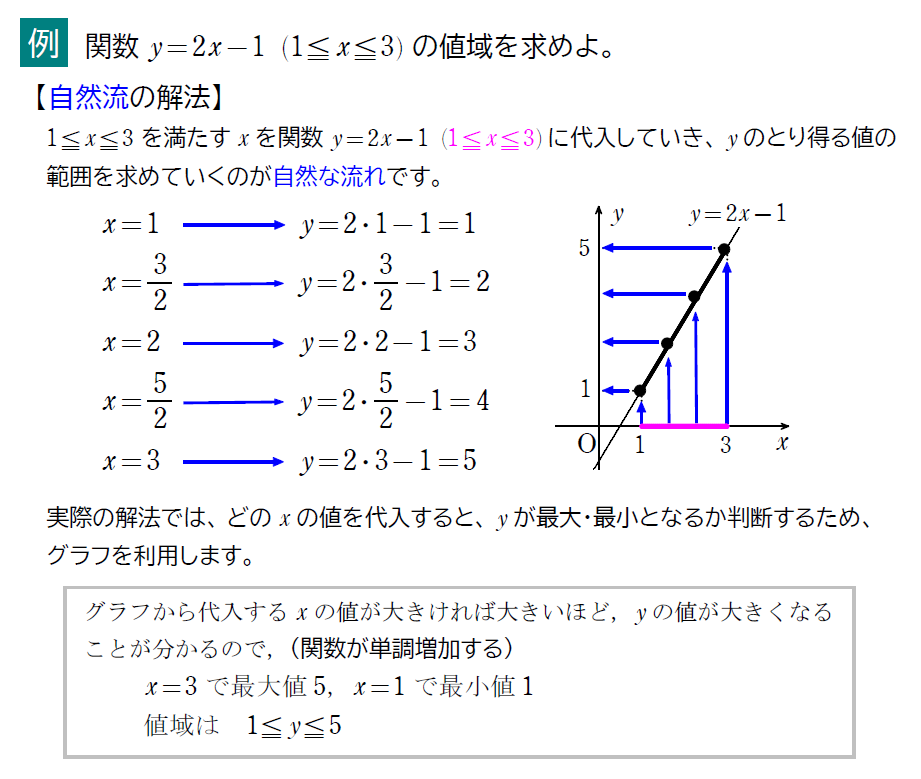
さて、続いては「逆手流」という手法を使った解法です。これが超絶重要な考え方になるので、必見です。
実数\(\small \,x,\,y\,\)が、\(\small x^2+y^2=2\) を満たすとき、\(\small x+2y\) の最大値・最小値を求めよ。

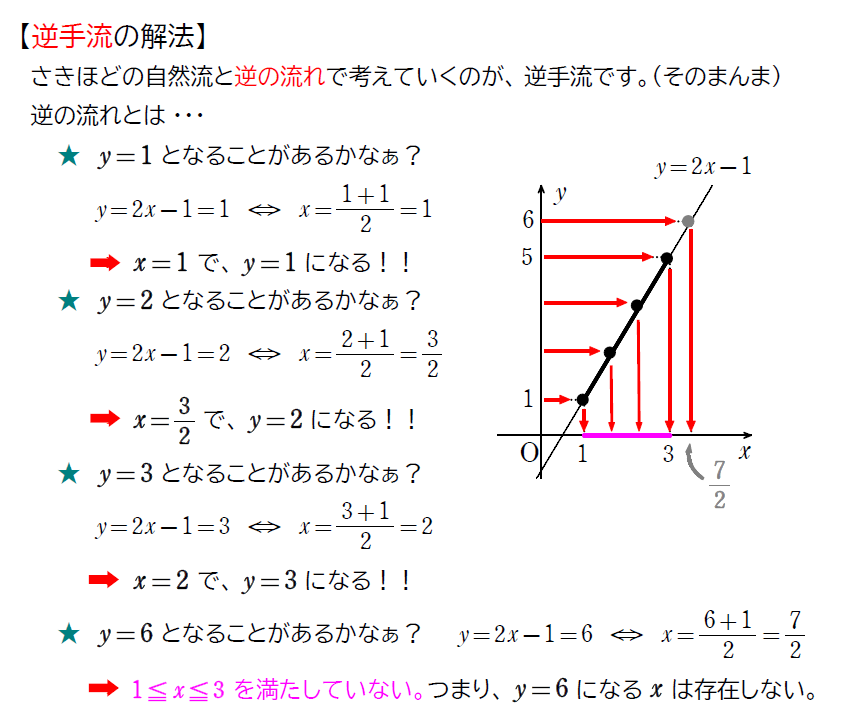
逆手流の説明は意外と長くなるので、詳しく知りたい方は下の「逆手流を詳しく説明」を開いてください。



2次不等式
続いては2次不等式・・・というよりは、2次方程式の応用問題です。
(この子が一番手がかかるかも・・・)
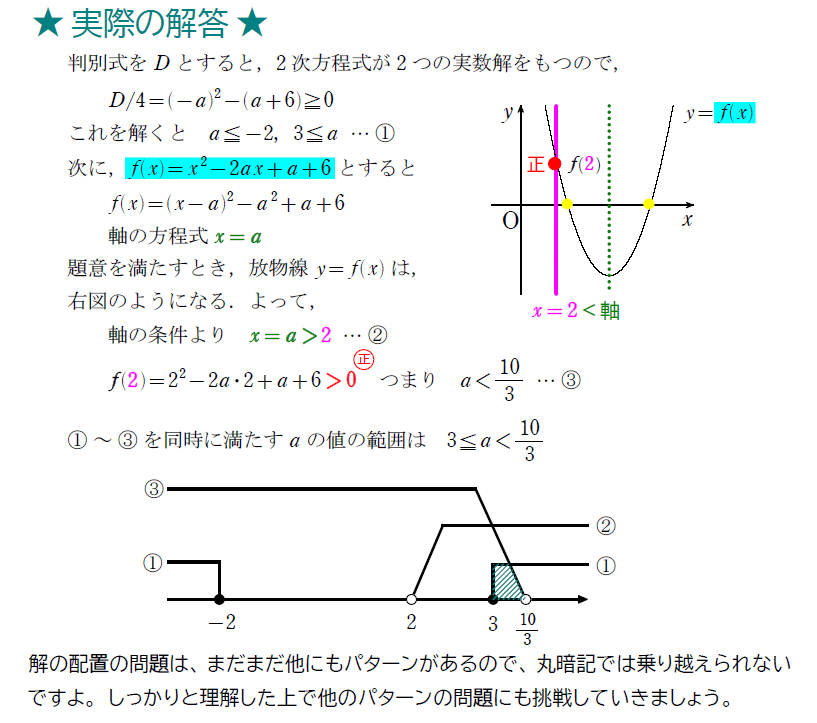
2次方程式 \(\small x^2-2ax+a+6=0\) の2解がともに \(\small 2\) より大きくなるような定数\(\small a\) のとり得る値の範囲を求めよ。
さて、ついに「解の配置」です。解答としては長くはないですが、丁寧に説明する分説明が長くなっているので、頑張ってみていきましょう。


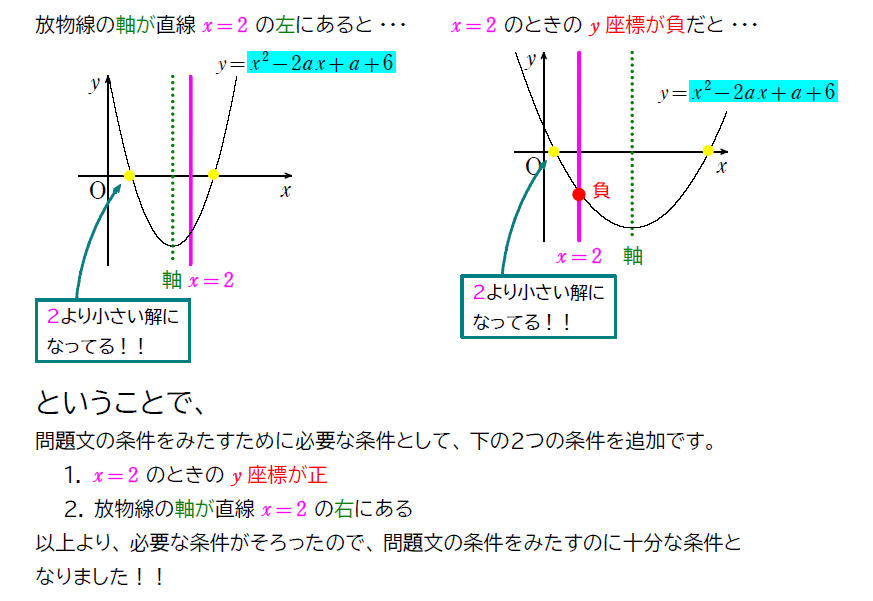
境界とは、問題文で解の大きさについて指示があった際、当てはまるかどうかの境界の事。
例:2解がともに3より大きい → 境界 \(\small \color{magenta}{x=3}\)
2解がともに1より大きく、2より小さい → 境界 \(\small \color{magenta}{x=1,\, 2}\)
2次方程式 \(\small x^2-4ax+a^2-6=0\) が正負の解をもつときの定数\(\small a\) のとり得る値の範囲を求めよ。

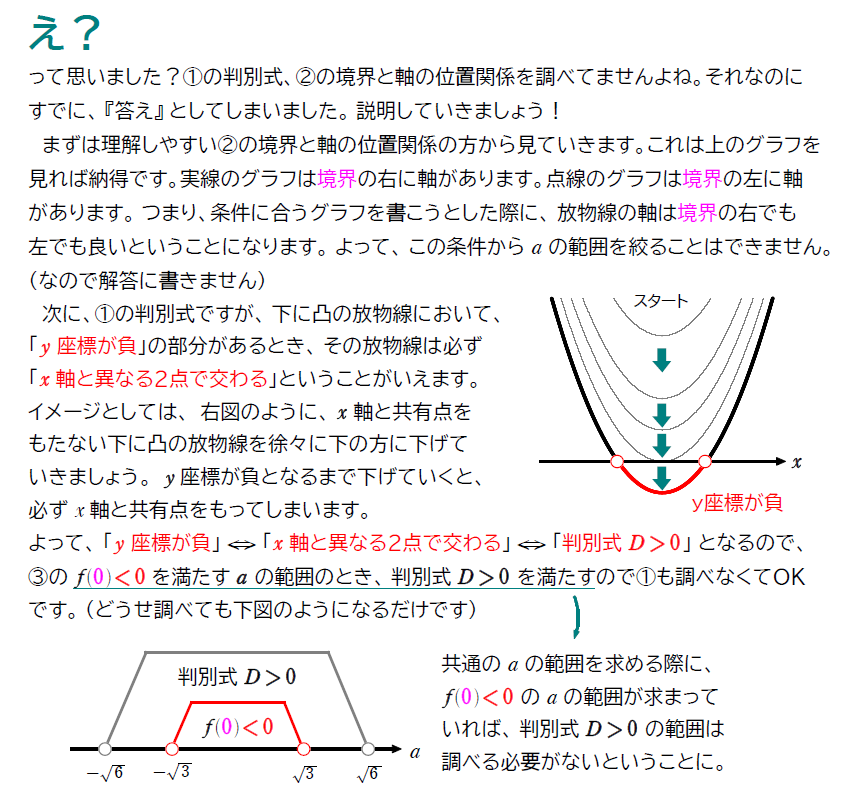
例題6のように③から調べた際に、\(\small y\,\)座標が負の部分があった場合、①②は調べなくて良い…ということを知っていれば、計算量を抑えられるので、覚えておきましょう!
まとめ!
2次関数の応用問題は、今回紹介した問題以外でも重要な問題はたくさんあります。紹介した応用問題をしっかりと理解していれば、他の応用問題にも対応できるようになるので、頑張りましょう!!







コメント