こんにちは。ねこの数式のnanakoです。
数Ⅰで三角比を学習したのを覚えていますか?
今回、学習する数Ⅱの三角関数は三角比の続きのような内容となります。
ラジアンという聞きなれないものも扱うことになり、数Ⅰの内容に比べると一気に難易度も上がるため、「高校2年生の内容に入った」というのを実感することになる人も多いと思います。
難しい内容ではありますが、一つずつ丁寧に理解していけば、必ずできるようになるので、あきらめずに頑張っていきましょう。
三角関数!
三角関数を学ぶ前に、角度の測り方を学びましょう。
一般角ってナニ?
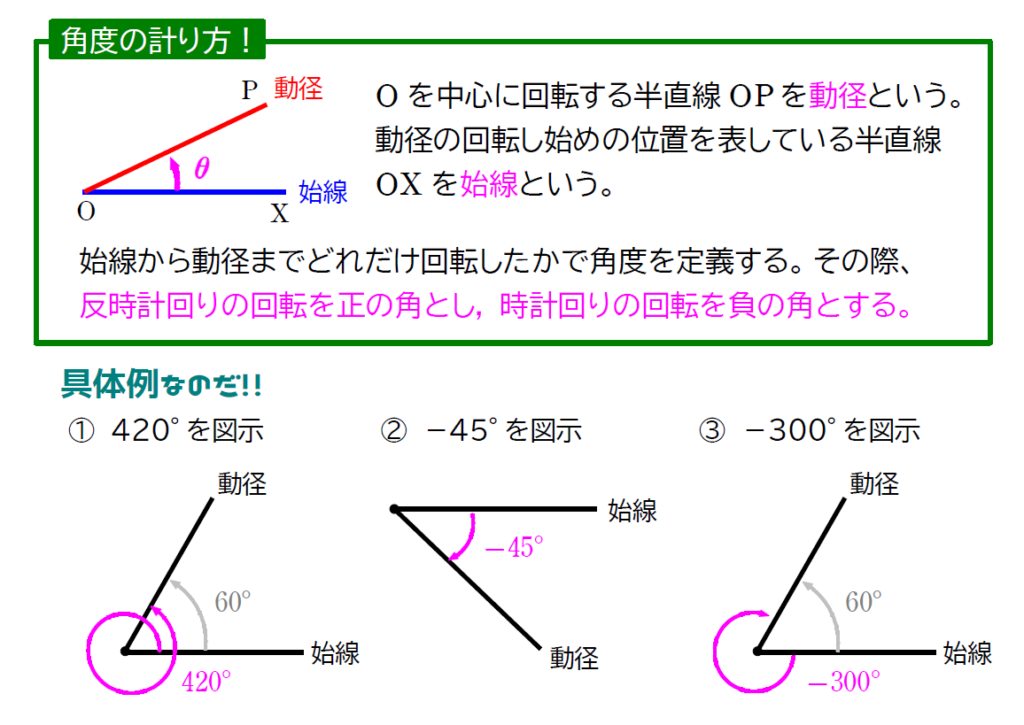
ところで、気づきましたか?
①と③の図は始線と動径のなす角(間の角)は同じ60°ですね。違う角度なのに同じ図になることがあるということになります。同じ図になる角度は他にも、780°,1140°・・・など、360°ずつ足したり引いたりしていけば無数に出てきます。
これらの360°を超える角度や負の角度に拡張する角が、一般角と呼ばれるものです。

さきほどの①と③の図で、一般角は 60°+360°×n (nは整数) と表せます。
さて、そろそろ本題の三角関数の話に入りたいのですが・・・
その前にもう少し角度について学習していく必要があります。そう!弧度法です!!
弧度法ってナニ?
2022年9月30日、日本列島に衝撃が走りました。
高校生御用達のマクドナルドが1年間で2回目となる値上げに踏み切りました。
いったい、ハンバーガーがいくらになったのか!?
なんと!
(約)1ドルです!!!!!
・・・
ピンとコーン・・・
まぁ、そうですよね。私たちは普段、『円』を利用して買い物をしています。なので、『ドル』で説明されても分かりづらいですよね(汗)
ただ、『円』も『ドル』も、値段を表すための単位なのは変わりません。
この『円』と『ドル』と同じような関係のものを学んでいきましょう。

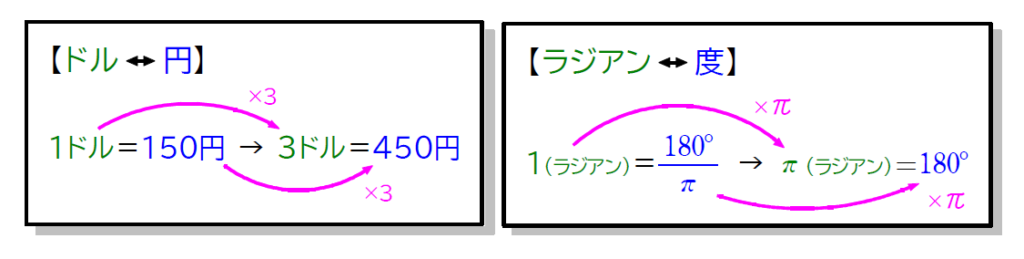
30°,60°など、『 ° (度) 』という単位を利用して角度を表す方法を『度数法』といいます。
それに対して、上の『ラジアン』という単位を利用して角度を表す方法を『弧度法』といいます。
この2つの単位『 ° (度) 』、『ラジアン』は換算ができ、それが180°=\(\small \pi \)(ラジアン)というわけです。イメージとしては、150円=1ドルといった感じです。
三角関数の値ってナニ?
よ、ようやく三角関数の話ができます・・・。
三角関数というのは、三角比のときに学習した sinθ,cosθ,tanθ を関数にしたものです。また、sinθ,cosθ,tanθ の値を三角関数の値といいます。
ちなみに、『三角比の値』と『三角関数の値』の違いは、あって無いようなものなので、同じものとして考えてもらってもかまいません。なので、定義としては三角比と同じで、
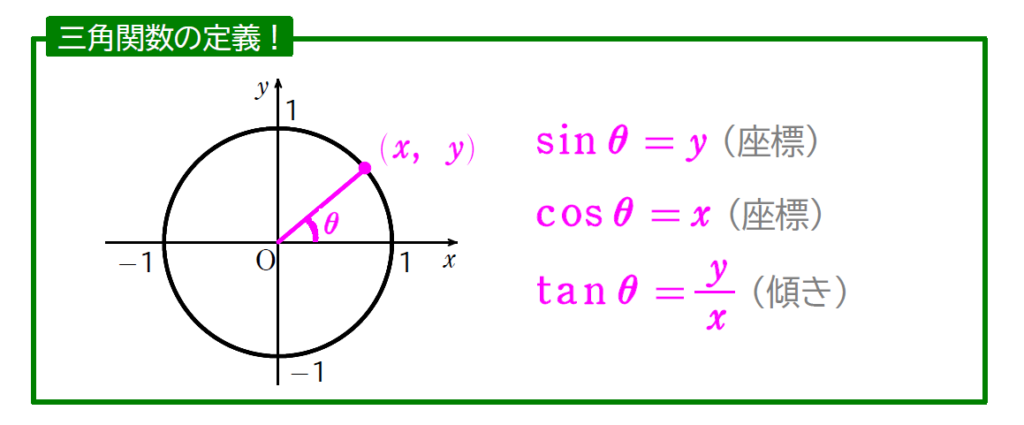
となります。
数Ⅰ三角比のときと同じように、数Ⅱ三角関数は『三角関数の値が九々のように答えられるようになるかどうか』で得意・不得意が明確に分かれます!
ここはじっくりと見ていきましょう。試しに\(\small \, \displaystyle \sin\frac{2}{3}\pi \,\)の値を求めてみます。
解説に入る前に先に結論を言います。今から紹介する解説は正しい求め方ではありますが、毎回解説通りに三角関数の値を求めるのは時間がかかって仕方ありません。そのため、あとで正しい求め方とは別に、『三角関数の値の覚え方』を紹介します。
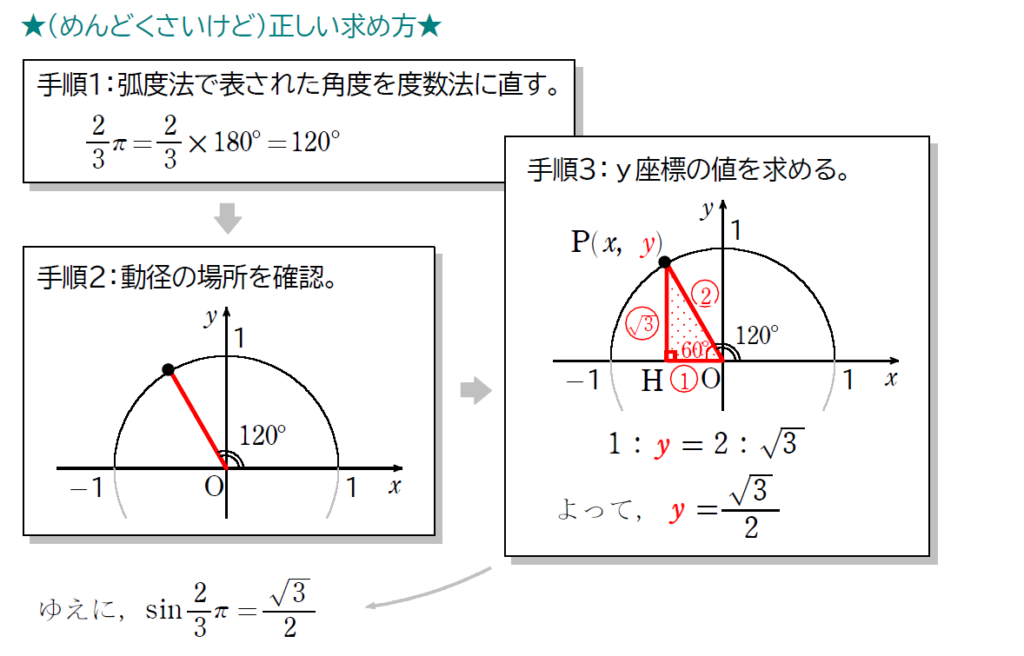
難しい説明ではなかったものの、この解法で毎回解こうとすると、三角関数の値を九々のように答えるのは難しいかもしれませんね。
三角比のときと同じように、動画で覚え方(求め方)を紹介していきます。
これから、ずっとお世話になる値なので、しっかりと練習しておきましょう。
下に4回分練習問題を用意しておきました。赤シートをお持ちでしたら、解答を開いて赤シートを利用すると、練習しやすいと思います。
(ちょっと透けちゃうので、画面の明るさを下げると良いですよ。)
何周もして、これからの内容に備えましょう。








三角関数の値について、方程式・不等式の簡単な問題を見てみましょう。
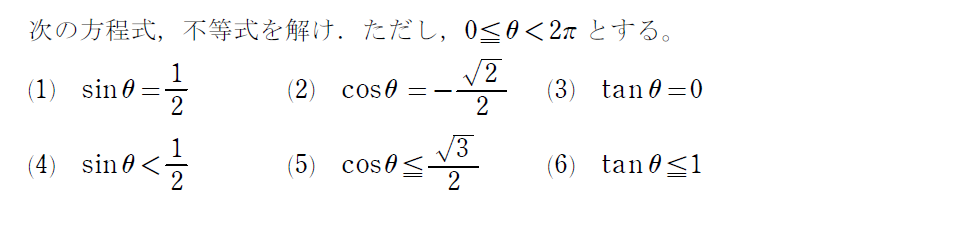
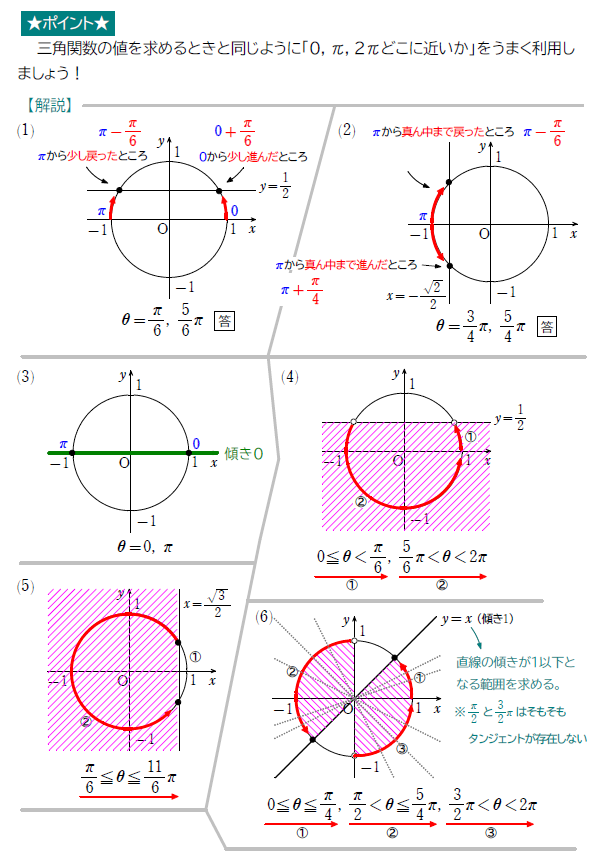
他のレベルの方程式・不等式は三角関数の公式を色々覚えた後にまとめて紹介したいと思います。それらの問題では例題2の内容を当たり前のように使うので、しっかりと理解しておきましょう。
三角関数の相互関係!
聞き覚えのある名前ですよね。
そうです。三角比のときにも出てきた『相互関係』を見ていきましょう。
相互関係ってナニ?
三角関数の相互関係とは、1つの三角関数の値が与えられた際に、残り2つの三角関数の値を求めることに利用します。
三角比のときと全く同じ公式になります。
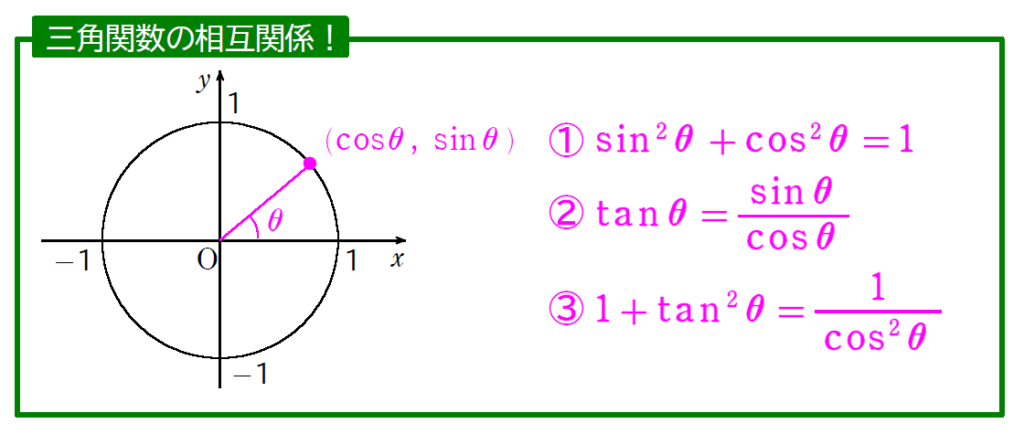
\(\small \displaystyle \sin \theta = -\frac{1}{3} \) のとき、\(\small \cos \theta \),\(\small \tan \theta \) を求めよ.




まとめ!
今回は「角度の測り方」「弧度法」「三角関数の値の求め方」「相互関係」を確認しました。
この後の内容は、すべてこれらの内容を九九のように扱います。
しっかりと反復練習をした上で、続きの内容を学習していきましょう。
ちなみに、数Ⅰ三角比の内容を復習したい人は下の記事を参考にしてください。







コメント