こんにちは。ねこの数式のnanakoです。
今回は順列・円順列の応用問題を紹介します。順列・円順列の基本を押さえたうえで、解法の判断が難しい問題などを紹介したいと思います。
目次!
順列の応用問題を紹介!
まずは順列の応用問題を紹介したいと思います。
もし基本問題に不安がある場合はこちらの記事を参考にしてください。
○桁の整数の応用問題ってナニ?
〇桁の整数を作る問題は先頭の位に0が来ないのがポイントでしたね。
今回は6の倍数の個数について見てみましょう。
例題1

解説

辞書式配列の応用問題ってナニ?
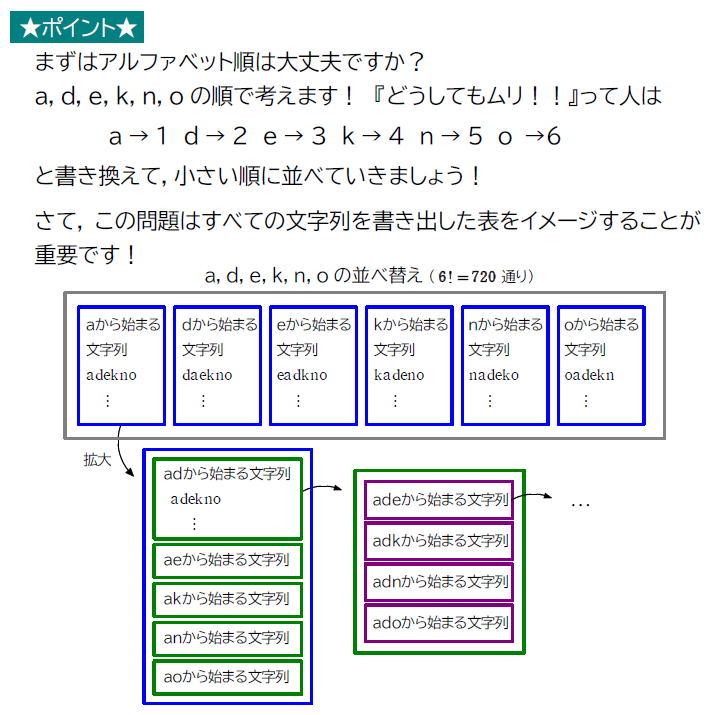
辞書式に並べた際に何番目?に関する問題です。
この問題は解答を理解するだけでも非常に難しい上に、自分で解けるようにするのはさらに大変な問題です。
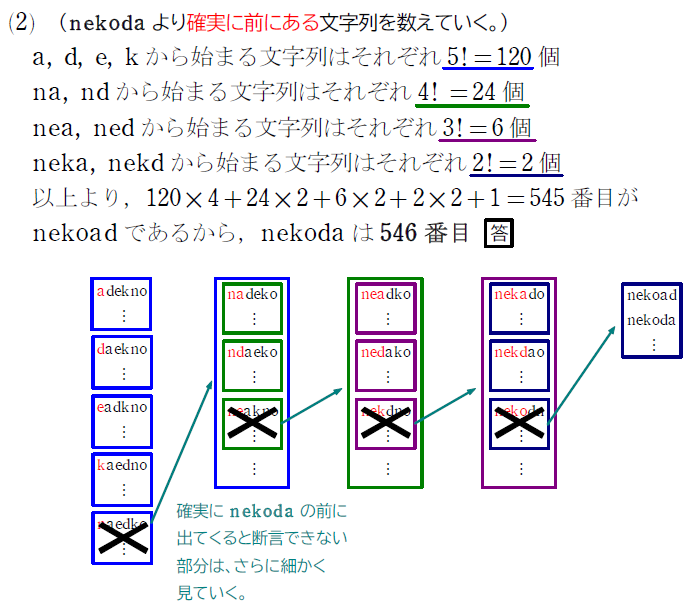
例題2

解説



円順列・数珠順列の応用問題
続いては円順列・数珠順列に関する応用問題を紹介したいと思います。基本が心配な人は下の記事を参考にしてください。
同じものを含む円順列ってナニ?
円順列と同じものを含む順列の融合問題です。
個数で対応が変わります。
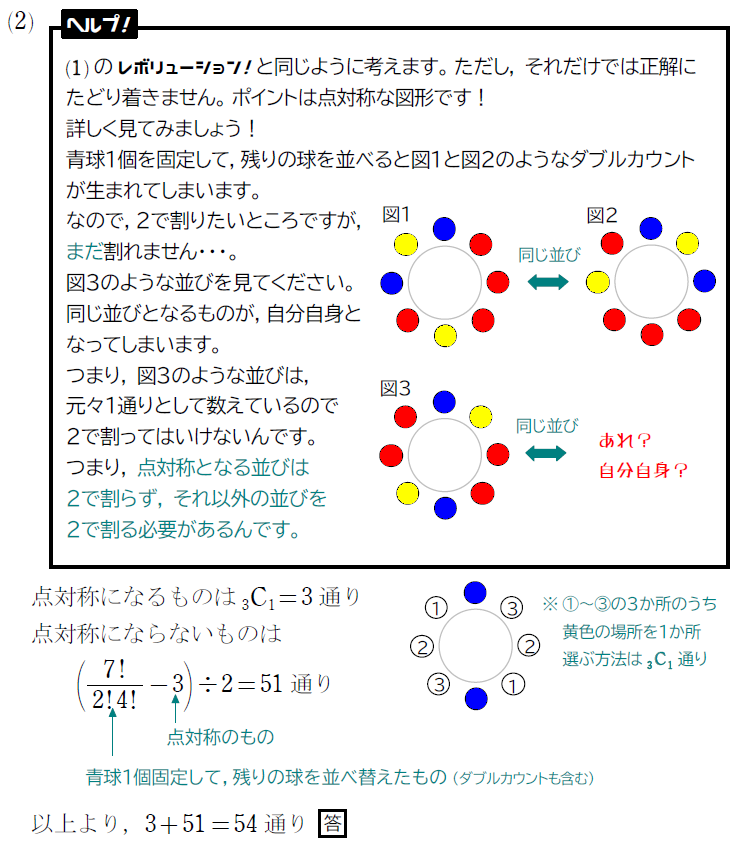
例題3

解説


同じものを含む数珠ってナニ?
数珠順列と同じものを含む順列の融合問題です。
ただ2で割れば良いというわけにはいかないので注意が必要です。
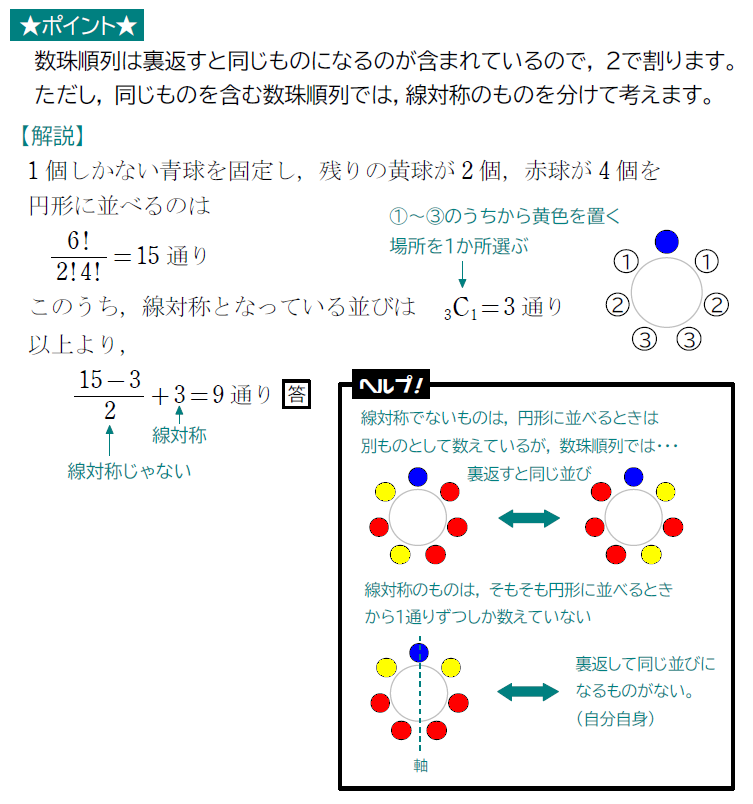
例題4
青球1個,黄球2個,赤球4個にひもを通して腕輪を作るとき,何通りできるか。
解説
立方体に色塗りの問題ってナニ?
例題4
立方体の各面を塗り分ける。ただし,塗り分けるというのは,隣り合う面を別々の色で塗ることをいう。次の問いに答えよ。
(1) 異なる6色で塗り分ける方法を答えよ。
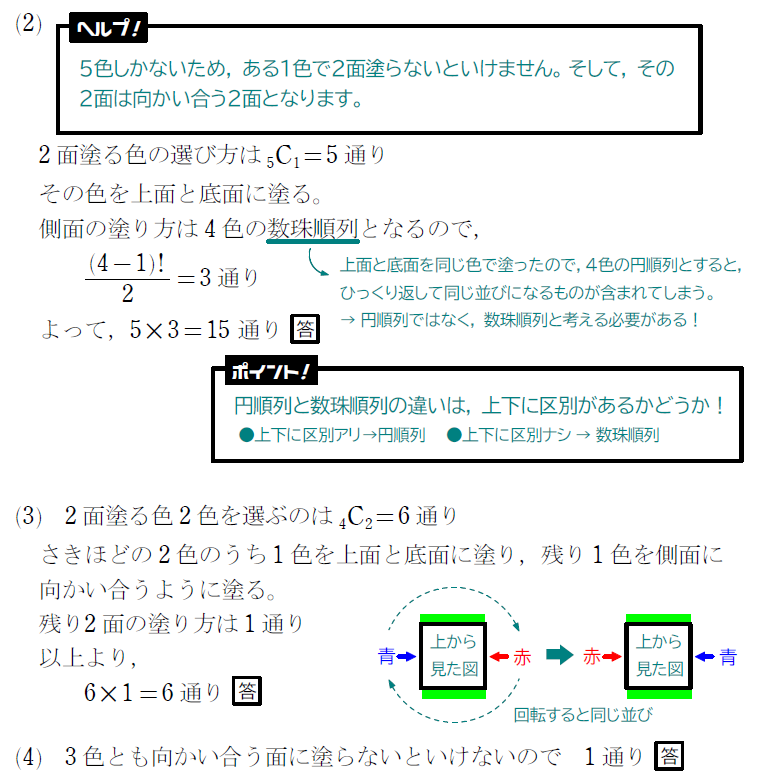
(2) 異なる5色で塗り分ける方法を答えよ。
(3) 異なる4色で塗り分ける方法を答えよ。
(4) 異なる3色で塗り分ける方法を答えよ。
解説

まとめ!
場合の数の応用問題はバリエーションが豊かです。
今回、紹介した問題以外にも経験してほしい問題は山ほどありますが、今回紹介した問題をしっかりと理解していれば、それらの問題にも対応できると思います。
頑張って復習しましょう!!






コメント