こんにちは。ねこの数式のnanakoです。
タイトルにツッコミを入れたい方はコメントへどうぞw
さて、今回は確率の問題です。中学のときにも確率は扱いましたが、高校では中学の内容よりも複雑な内容となります。試行やら事象やら聞きなれない用語も出てきますが、一つずつ理解していきましょう!
確率を紹介!
同様に確からしいってナニ?
まずは『確率』とは何なのかを再確認していきましょう!
『Aが起こる確率』とは、Aが起こる頻度の割合のことです。
例えば、さいころを1回振って6の目が出る確率は \(\small \displaystyle \frac{1}{6} \) です。これは6回に1回の頻度の割合で起こるという意味です。
では、確率をどう求めるか(定義)を確認していきましょう!
「知ってるよ!」っていうツッコミが入りそうですが、ここ重要なので飛ばさずに必ず読んでください!

はい、さっぱり意味がわかりませんね。具体例を利用して解説していきましょう!
(赤字とピンクのラインのところだけは覚えましょう。あとは…ふ~んで大丈夫です。)
ということで、上の例だと、
全事象の根元事象は「1の目が出る」「2の目が出る」…「6の目が出る」で、その個数は6個(通り)です。
3の倍数の目が出るという事象の根元事象は「3の目が出る」「6の倍数の目が出る」で、その個数は2個(通り)です。
よって、確率は \(\small \displaystyle \frac{2}{6}=\frac{1}{3} \) となります。
なので、確率は以下のような説明をする人が多いと思います。

中学の際に習った公式でしたかね?気になるのは赤字の部分です。これも具体例で見ていきましょう!
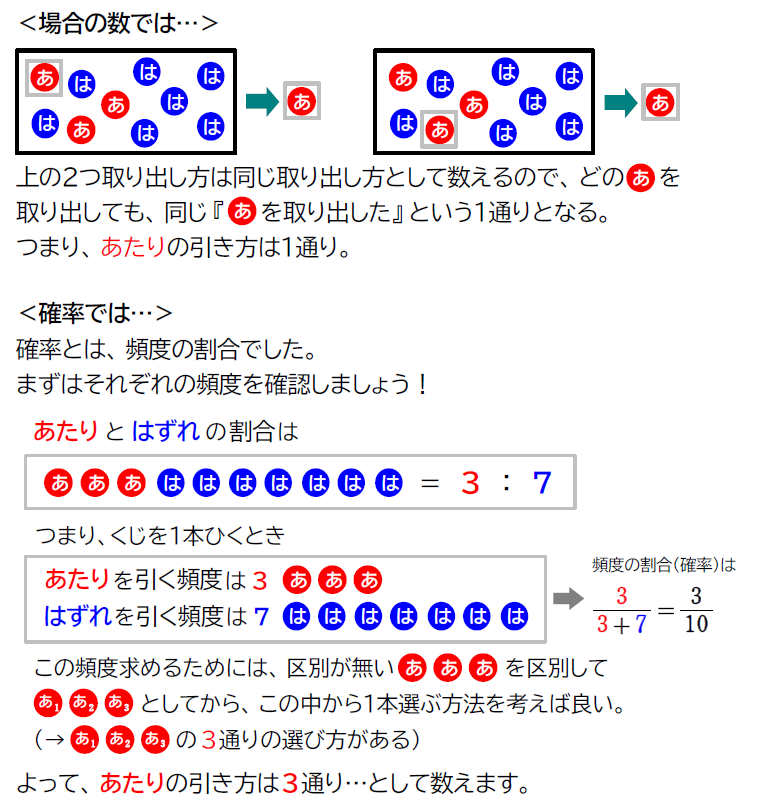
問.10本中あたりが3本入ったくじの中から1本引くとき、あたる確率を求めよ。
\(\small \displaystyle \frac{3}{10} \) でしょ! と即答されそうですが、まさにその通りです。
では、次の解答はどう思いますか?
くじの引き方は「あたりを引く」「はずれを引く」の2通り。あたるのは「あたりを引く」という1通り。よって、確率は \(\small \displaystyle \frac{1}{2} \) となる…
答えが間違っているのは確かですが、なぜ間違っているか分かりますか?
結論から言うと、『確率』での何通りの求め方は『場合の数』での何通りの求め方と違うからです。

排反?余事象?ってナニ?
まずは排反から紹介します!

続いては余事象の紹介!

では、実際の問題を見てみましょう!
袋の中には赤球が3個、白球が4個入っている。この中から3個の球を同時に取り出すとき、次の問いに答えよ。
(1) 赤球2個、白球1個となる確率を求めよ。
(2) 取り出した球が3個とも同色である確率を求めよ。
(3) 白球を少なくとも1個取り出す確率を求めよ。

ちなみに(3)は白球が1個(赤球が2個)の確率、白球が2個(赤球が1個)の確率、白球が3個(赤球が0個)の3つの確率を足しても出せます。(めんどくさいですが…)
男子2人と女子4人が一列に並ぶとき、両端が女子または男子2人が隣り合う確率を求めよ。

独立試行と反復試行を紹介!
独立試行ってナニ?
まずは試行という言葉から確認しましょう!
試行とは、『さいころを振る』や『袋の中から球を取り出す』など「偶然によって結果が決まる実験や観測のこと。」のこと。
まぁ、ざっくり言うと、問題文で指定している作業のことです。
では、本題の独立試行の説明を見ていきます!
独立試行とは、2つの試行の結果がお互いに影響しあわないことをいいます。
排反と似ていますが、違うものです。。。
同時に起きないという意味では同じですが、事象についてのときは「排反」、試行についてのときは「独立試行」と使い分けます。用語がテストに出るわけではないので、今は『ふ~ん』くらいでも大丈夫です(笑)
重要なのは、次の公式!

では、例題を見てみましょう!
Aの袋の中には赤玉が3個と白玉が2個、Bの袋の中には赤玉4個と白玉2個入っている。Aの袋から1個、Bの袋から2個玉を取り出すとき、次の問に答えよ。
(1) 取り出した玉が3個とも赤である確率を求めよ。
(2) 取り出した玉が3個が同色である確率を求めよ。

反復試行ってナニ?
反復試行とは、同じ試行を繰り返しすること。反復試行は公式があるのですが、丸暗記するより仕組みを理解した方が解きやすいので、例を見ながら紹介していきます!
1個のさいころを5回振るとき、次の確率を求めよ。
(1) 偶数の目が5回出る確率
(2) 3の倍数の目が1回だけ出る確率
(3) 4以下の目が3回だけ出る確率




条件付き確率を紹介!
条件付き確率ってナニ?
条件付き確率とは、条件をクリアした上で起こる確率のことです。
具体例で見ていきましょう!


さてさて、このくらいの問題であれば公式など必要ありませんが、難しい問題となったときのために公式を紹介していきましょう!

では、例題で確認していきましょう!

(1)は普通の確率、(2)は条件付き確率です。(2)は上の公式は使わなくても解けるので★の方を利用して解きましょう。

積の法則
今回はさっそく公式を見ていきましょう!




期待値を紹介!
期待値ってナニ?
「期待値が高い!」ってな言葉を聞いたことがあるんじゃないですか?
『期待値』とは、どれくらい期待できるかって値です。要するに平均みたいなものだと思ってください。


では、例題!
袋の中には赤球3個、白球4個入っている。この中から3個球を取り出すとき、取り出した赤球の個数の期待値を求めよ。

まとめ!
確率の問題の解き方は確立できましたか、笑。
同じ系統の問題でも、条件を少し変えると解けない…なんてこともあるので、今回紹介した問題をしっかりと理解した上で、類題をいっぱい解いて理解を深めていきましょう。
場合の数が心配な人は、下の記事から復習してみるのも良いと思います。頑張りましょう!





コメント