こんにちは。ねこの数式のnanakoです。
今回は、三角関数の最大最小の問題を中心に紹介していきたいと思います。
三角関数の公式や、三角関数の合成を利用するので、心配な人は下の記事を参考にしてください。また、方程式・不等式の問題と同じように解くことが多いので、それらの内容が不安な人も、下の記事を参考にしてください。
三角関数の最大最小の定番問題!
どの単元でもそうですが、最大値・最小値の問題は、方程式・不等式の問題と同じような考え方をすることが多いです。
実際に見てみましょう。
2次関数の最大最小にすり替えってナニ?
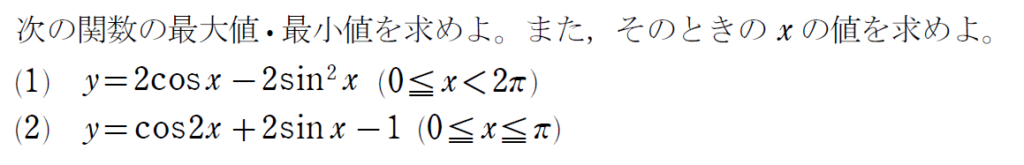
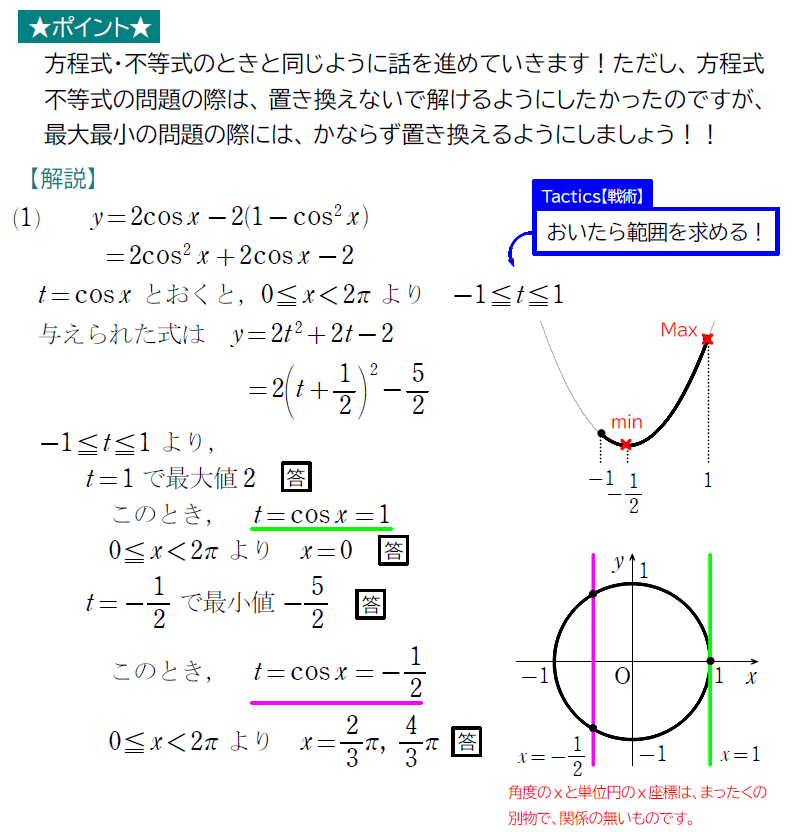
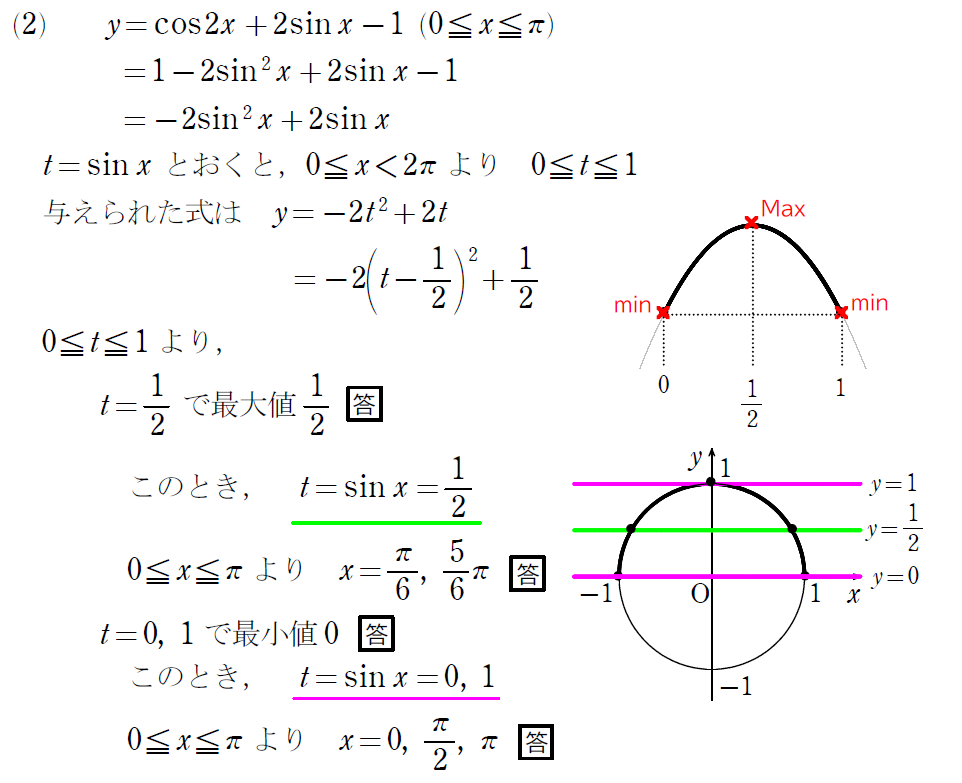
どうでしたか?
方程式・不等式の際には、2次方程式・2次不等式につなげましたが、最大最小の問題では、2次関数の最大最小の問題につなげました。
上の例題は、方程式・不等式の問題とセットで復習しておきましょう。
合成を利用した最大最小ってナニ?




(3)の角度が出せない状況での対応は、問題によっては \(\small \theta = \) ○ を代入するという回避方法が選べないこともあるので、※の方法も念のためにおさえておきましょう。
この合成を利用した最大値・最小値の問題は、応用問題でもよく使うものとなるので、しっかりと練習しておきましょう。
三角関数の最大最小の応用問題!
まずは置き換えを利用して2次関数の最大最小につなげる問題の応用問題です。例題1の上位互換というイメージです。
\(\small \sin \theta \) と \(\small \cos \theta \) について、対称性があるのがポイントになります。
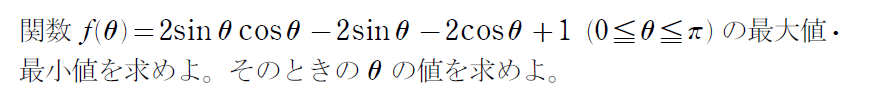

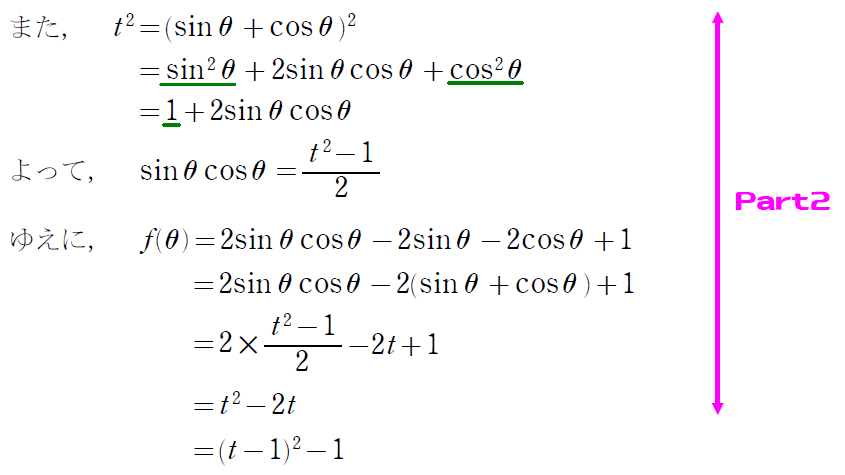
少し複雑に感じますかね?
Part1~Part3の3つのパート分けて理解しましょう。
- Part1置いたものの範囲を調べる!
\(\small \sin \theta + \cos \theta \) の範囲(最大最小)を求めたいので、合成する。
- Part2与えられた関数をtを用いて置き換え!
2乗して \(\small \sin \theta \cos \theta \) をtで表すのがポイント。
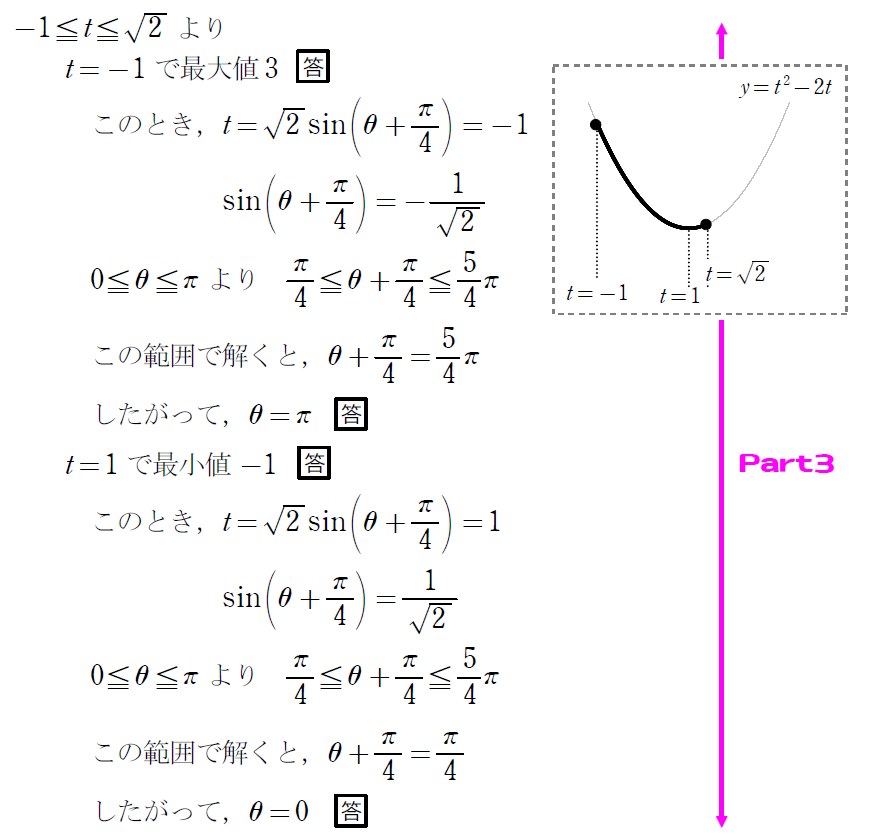
- Part3最大最小を求める!
置き換えた式が2次関数となっていれば平方完成で求まります。
ちなみに、\(\small f( \theta )=t^2-2t \) という式に違和感を感じた人はいましたか?
\(\small f( \theta ) \) は \(\small \theta \) の関数という意味なので、「\(\small t^2-2t \) とイコールというのはおかしい」と考えた人もいたのではないでしょうか?
この \(\small f( \theta )=t^2-2t \) という式は、左辺の \(\small f( \theta ) \) は \(\small 2 \sin \theta \cos \theta -2 \sin \theta -2 \cos \theta +1\) のことで、\(\small 2 \sin \theta \cos \theta -2 \sin \theta -2 \cos \theta +1\) と \(\small t^2-2t \)は等しいという意味になります。
さて、続いては例題2の上位互換みたいな問題を見てみましょう。
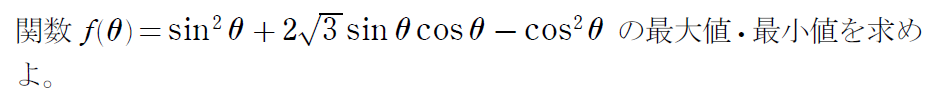

今回の問題では \(\small \theta \) に範囲がありませんが、範囲が与えられていた場合は、\(\small \theta \) の範囲から \(\small \displaystyle 2 \theta \, - \frac { π }{6} \) の範囲を求め、\(\small \displaystyle \sin \left( 2 \theta \, ー \frac{π}{6} \right) \) の最大値・最小値を求める流れになります。
例題3と例題4は似ているような式なのでセットで復習しましょう。
共通点は \(\small \sin \theta \cos \theta \) が含まれている。違いは・・・
例題3 → サインとコサインに対称性がある。
例題4 → \(\sin ^2 \theta \) または \(\cos ^2 \theta \) がある。
まとめ!
三角関数の最大値・最小値の問題はいかがでしたでしょうか?
方程式・不等式の問題とつながりが強い問題ばかりなので、一緒に復習すると効率が良いと思います。
また、さらなる応用問題を勉強する上では、今回紹介した内容は当たり前のように使うものばかりなので、しっかりと復習しておきましょう!






コメント