こんにちは。ねこの数式のnanakoです。
今回は、三角関数の応用問題を入試レベルまで紹介していきたいと思います。
けっこう難しい問題もあるので、基本的な内容をしっかりと復習してから学習しましょう!
2倍角の公式、半角の公式、和積・積和の公式などの確認はこちら↓
三角関数の合成を利用した方程式などの確認はこちら↓
三角関数の最大値・最小値の問題の確認はこちら↓
入試レベルの問題を紹介!
今回紹介する入試レベルの問題は、どれもこれも有名なものばかりなので、入試までに一度は経験しておきたい問題です。
また、これらの応用問題をただ解けるように復習するだけでなく、他の応用問題も解けるようにするために、仕組みをしっかりと理解しましょう。
方程式の解の個数ってナニ?
まずは方程式の解の個数にまつわる問題です。方程式の解の個数は入試でも人気のテーマです。
三角関数の方程式の問題では、置き換えを利用することがほとんどですが、置き換えた際の方程式の解の個数は、注意する点がいくつかあるので見ていきましょう。

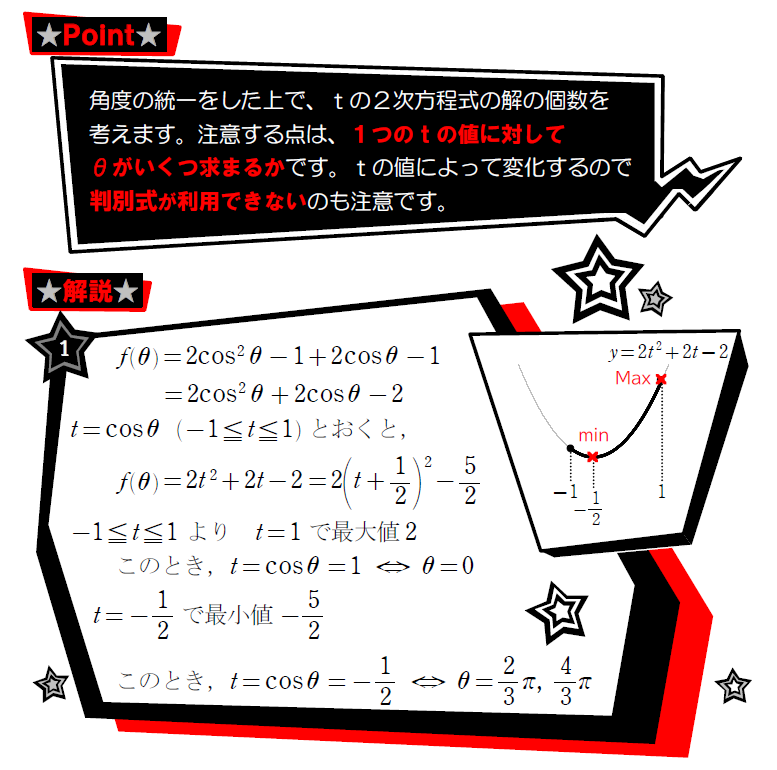
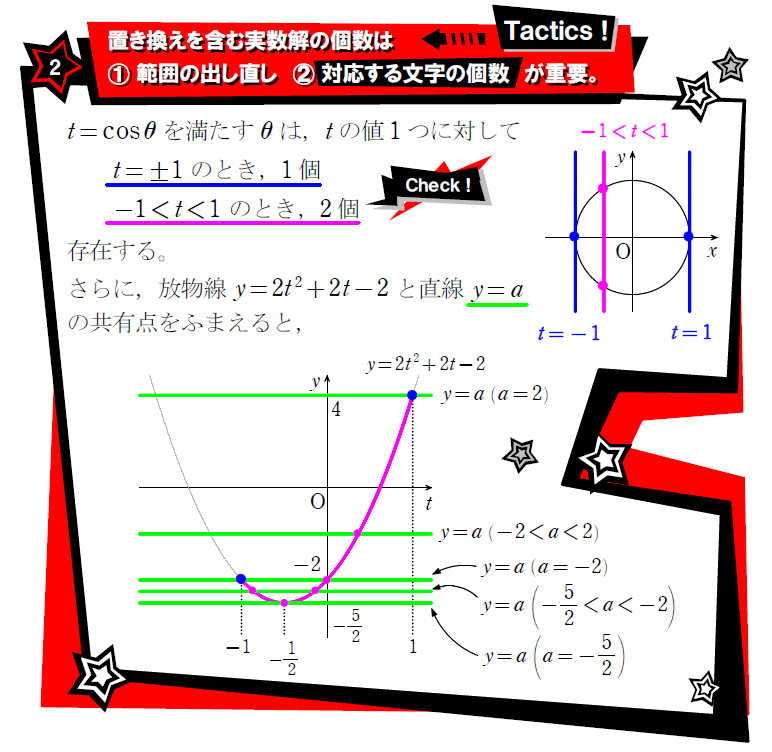

解の個数なので、判別式を利用したいところではありますが、判別式でtの個数が分かっても、どのようなtの値かでθの個数が変化してしまうため、判別式では対応できません。
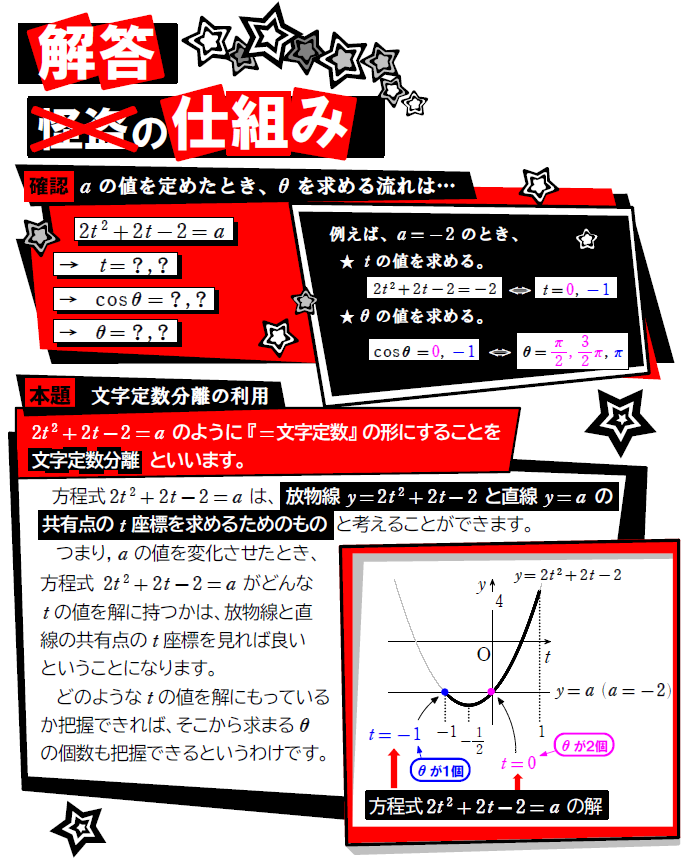
グラフを利用する際には、文字定数の入っている場所によって、グラフの把握のしやすさが変化します。今回利用した文字定数分離は、未知の定数である \(\small a \) が放物線の式に含まれていると、グラフの様子が分かりづらいので、分離することにより状況の把握をしやすくする考え方です。
色々な単元で利用することとなるのでしっかりと押さえておきましょう。
三角関数の分数式の最大最小ってナニ?
続いては、三角関数の分数式の最大値・最小値の問題です。誘導が無くても対応できるようにしたいです。
また、誘導を無視した別解を紹介しますが、数Ⅱ図形と方程式の内容を利用するので、まだ学習していない人は別解は無視してください。学習済みの人は別解も必ず確認しておきましょう!

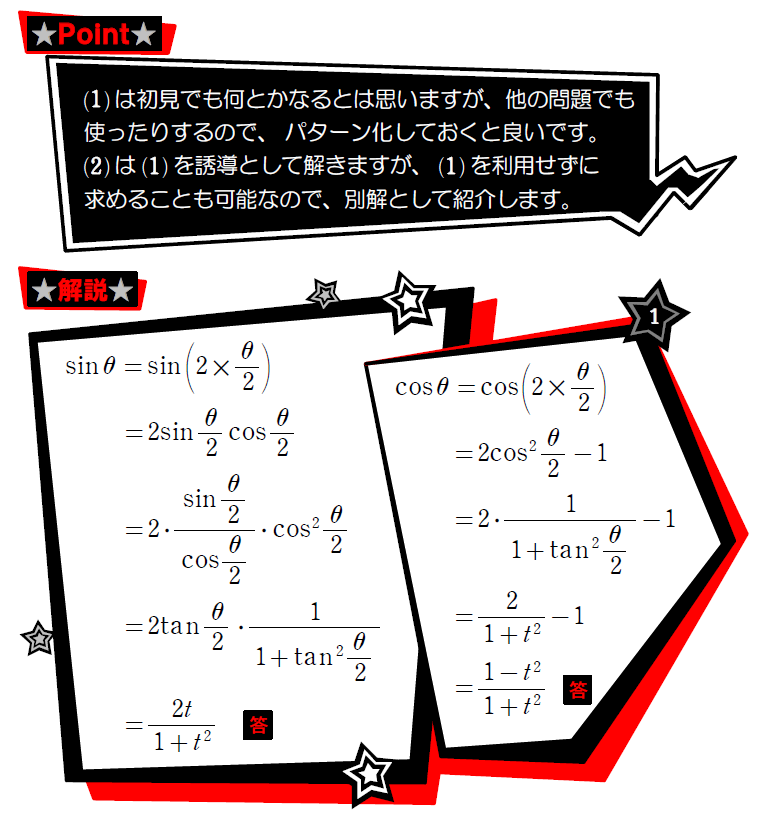
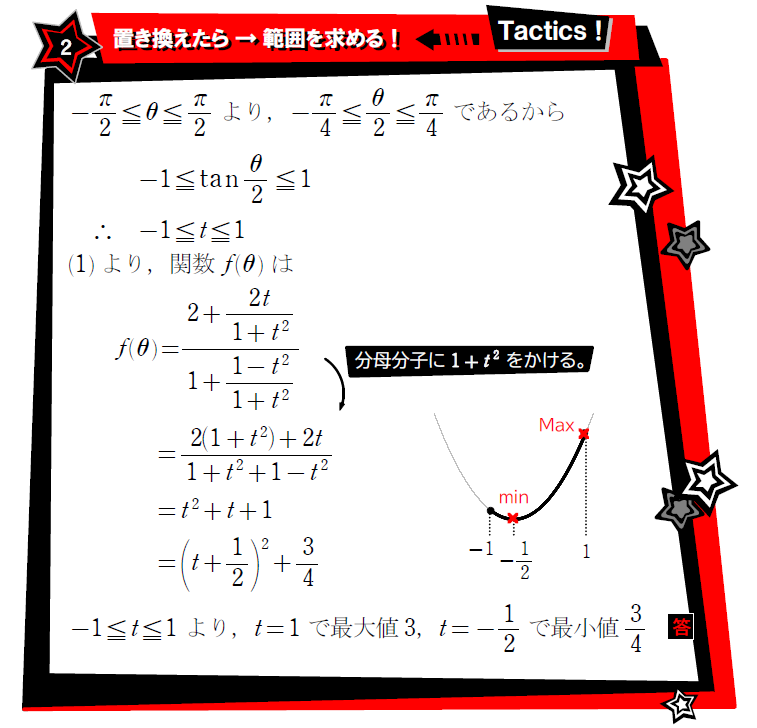
ここからは数Ⅱ図形と方程式の内容を学習した人のみ確認しましょう!

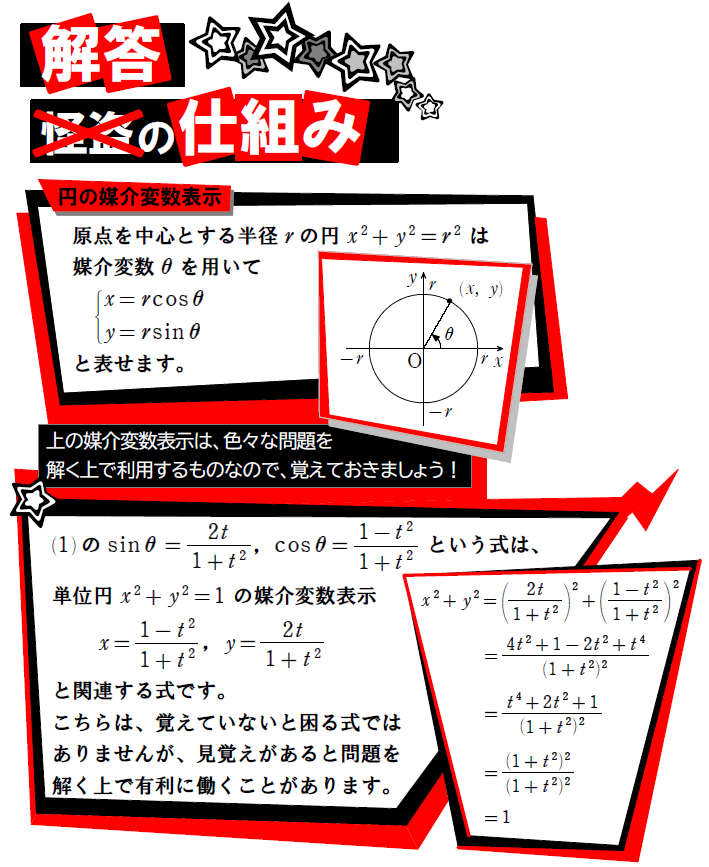
補足としては、分数式の最大・最小はこの単元に限らず3択がすぐに浮かぶようにしておきましょう。
上の3択の優先順位は第1位は圧倒的大差で相加相乗平均の関係です。利用頻度は他と大きく変わるわけではないですが、利用できたときの解答の短さは圧巻です。
利用できるかの判断も簡単に済むので、まず『相加相乗平均の関係が利用できるか』を確認して、利用できない場合は、他の2択を考えるという流れが良いかと思います。
逆手流については下の記事を参考にしてください。
三角関数の連立ってナニ?
三角関数の連立の問題です。ネタバレするので多くを語らず例題に入りましょう・・・



\(\small \sin^2 \theta + \cos^2 \theta =1 \) を利用して一文字消去は色んなシチュエーションで使うので、すぐに頭に浮かぶようにしておきましょう。
\(\small \sin \theta \) と \(\small \cos \theta \) を結びたいときには、\(\small \sin^2 \theta + \cos^2 \theta =1 \) と覚えておきましょう!
和積の公式を利用した方程式ってナニ?
次の例題は和積の公式を利用した方程式ですが、ただ公式を利用すれば良いわけではないです。誘導をどう利用するかがポイントとなります。
数Ⅱ方程式・式と証明の知識を利用するので、未習の人は(2)を飛ばしてみてください。



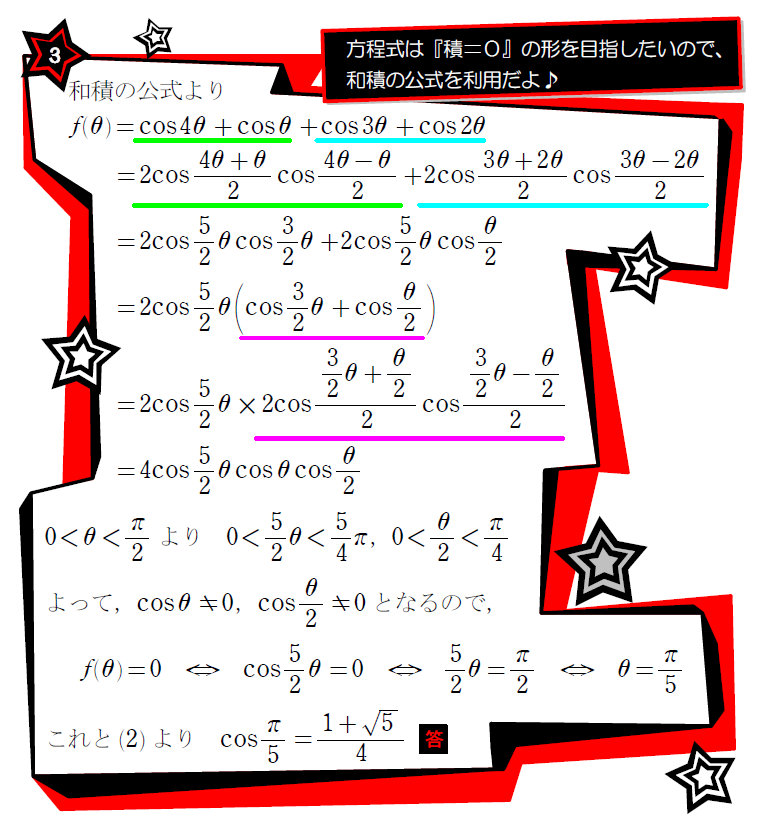

和積を利用して解く方法、倍角を利用して解く方法、問題によってはどちらを利用しても方程式の解が求まることもあります。
今回は一つの方程式を2通りの解法で解くことで、未知の \(\small \displaystyle \cos \frac{π}{5} \) の値を挟み込むように求めるという華麗な問題でした。
まとめ!
三角関数の入試レベルの問題はいかがでしたか?
これまで習ってきた数学の知識を利用する問題ばかりで復習のしがいがありますね♪
紹介したい応用問題はまだまだありますが、今回紹介した応用問題は有名な問題であり、色々な事が学べる良問なので、いち早く復習して解けるようにしていきましょう。







コメント