こんにちは。ねこの数式のnanakoです。
この単元では、複雑な計算や難しい記号などが出てくるわけではなく、数学的な考え方や議論の仕方などを学習します。
解き方を丸暗記するのではなく、一つひとつ丁寧に考えないと解けない問題ばかりです。
この単元で数学的な考え方を養って、これからの高校数学を学ぶ上で必要となる思考力をつけていきましょう。
命題
まずは天空の城ラピュタの画像とともに、いくつかセリフを見てもらいましょう。

「ロボットにより通信回路が破壊された。」
このセリフはムスカの本性をよく表しています。自分の部下に通信ケーブルを切断させておいて、白々しくこんなセリフを言えてしまう。ある意味尊敬できます。

「お前を助けるためにおどかされてやったに決まってるじゃないか!!」
これはムスカによりシータがさらわれた後、ドーラがパズーに向けて言った一言です。
実際、このセリフの前にムスカはシータに対して「あの少年の運命は君がにぎっているんだよ」と脅しています。

屋上から飛び降りて、天井を突き破りながら下の階まで落ちた後のシーンです。
普通なら死んでますが、パズーは「ぼくの頭は、親方のゲンコツより、かたいんだ。」で済ませています。パズーは人間離れした行動をすることが多いですね。
さて、そろそろ本題に入りましょう。今回紹介した3つの文章ですが、
- 「ロボットにより通信回路が破壊された。」
- 「お前を助けるためにおどかされてやったに決まってるじゃないか!!」
- 「ぼくの頭は、親方のゲンコツより、かたいんだ。」
1は嘘(正しくない)でした。2は正しかったです。3は…これは判断ができませんね(笑)
1や2のように明確に「正しい」「正しくない」がはっきり決まる文章や数式を『命題』といいます。3のように明確に正しいかどうかがはっきりと決まらないものは命題とは言えません。
今回はこの命題について見ていきたいと思います。
命題の真偽と反例ってナニ?
命題が正しいとき「命題は真」、命題が正しくないとき「命題は偽」といいます。命題が偽の際、正しくない例のことを反例といいます。
次の命題の真偽を答えよ。また、偽の場合は反例も答えよ。
\(\small(1)\) \(\small x=3 \ \)ならば\(\small \ x^2=9\ \)である。
\(\small(2)\) \(\small x^2=4\ \)ならば\(\small \ x=2\ \)である。
\(\small(1)\) \(\small x=3\ \)の両辺を2乗すると、\(\small x^2=9\ \)となるので真。
\(\small(2)\) \(\small x^2=4\ \)より、\(\small x=\pm2\ \)となるので偽。
反例は、\(\small x=-2\)
命題「\(\small x=3 \ \)ならば\(\small \ x^2=9\ \)である。」は真となりましたが、これを記号で表すと、「\(\small x=3 \ \Rightarrow \ x^2=9\ \)」と表します。「\(\small \Rightarrow\)」「\(\small \Leftarrow\)」は成立する向きを表していて、「\(\small x^2=1\)」と「\(\small x=\pm1\)」のように「左から右」「右から左」どちらも成立する際には、「\(\small \Leftrightarrow\)」を利用して「\(\small x^2=1 \ \Leftrightarrow \ x=\pm1\)」と表します。
また、\(\small x=3\) や \(\small x^2=9\) などは条件というので、頭の片隅に置いておいてください。
『命題』や今後紹介する『必要条件・十分条件』『逆・裏・対偶』が難しくて分からないという話をよく聞きますが、その原因の大半が「真・偽の判断がついていかない」からです。
「真・偽の判断」は数学的な力も必要ですが、感覚(コツ)をつかむことが重要です。
命題『\(\small \,\color{blue}{p} \ \Rightarrow \ \color{magenta}{q}\,\)』の真偽の判断の仕方は、\(\small p\,\)は自分がもっている条件、\(\small q\,\)は相手からの質問と考えると正確に判断できます。もう1つ例題をみてみましょう。
次の命題の真偽を答えよ。また、偽の場合は反例も答えよ。
\(\small (1)\) \(\small |x|<3\) ならば \(\small x<3\)
\(\small (2)\) △ABCが二等辺三角形ならば、∠B=∠C
\(\small (1)\) \(\small |x|<3\) の絶対値を外すと \(\small \color{blue}{-3<x<3}\) となり、これが自分がもっている条件です。
このとき、「それって絶対に \(\small \color{magenta}{x<3}\) を満たすの?」って聞かれたと思ってください。
どうですか?満たしてますよね?
ということで真となります。
\(\small (2)\) △ABCが二等辺三角形が自分のもっている条件です。これに合う三角形をすべて考えたときに、
「それって絶対に ∠B=∠C なの?」って聞かれたら、どうですか?
∠A=∠Bの△ABCもありますよね。なので、偽となります。
相手からの質問として考える時に「絶対に○○?」のように「絶対に」をつけて考えるのも、ポイントの1つとなります。
包含関係ってナニ?
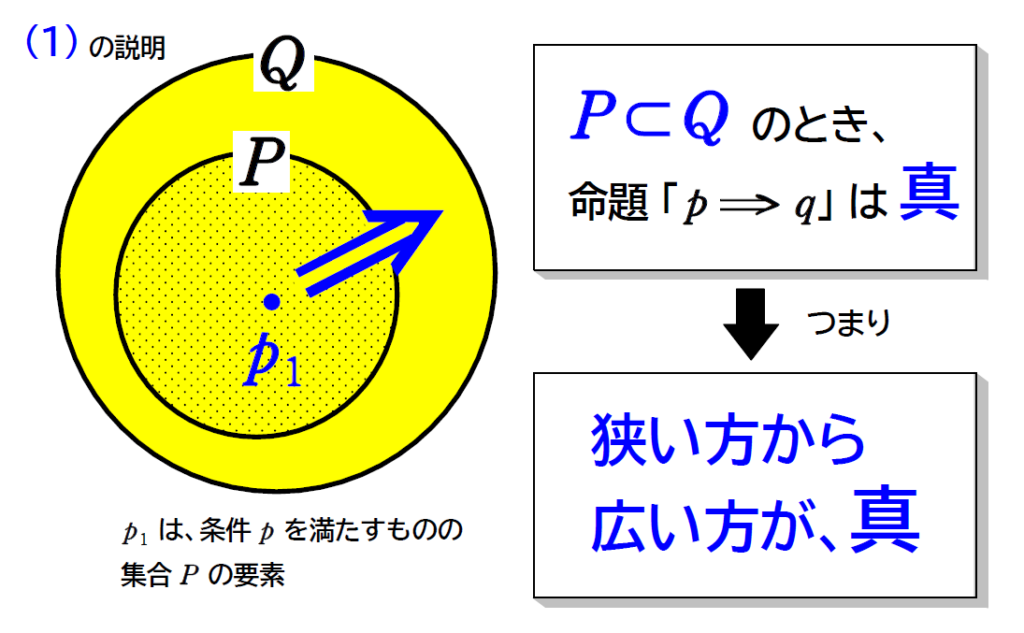
集合\(\small \,P\,\)が集合\(\small \,Q\,\)の部分集合となるとき、つまり、集合\(\small \,P\,\)が集合\(\small \,Q\,\)の中にスッポリと収まるとき、2つの集合の関係を包含関係といい、\(\small P\subset Q\ \)と表します。
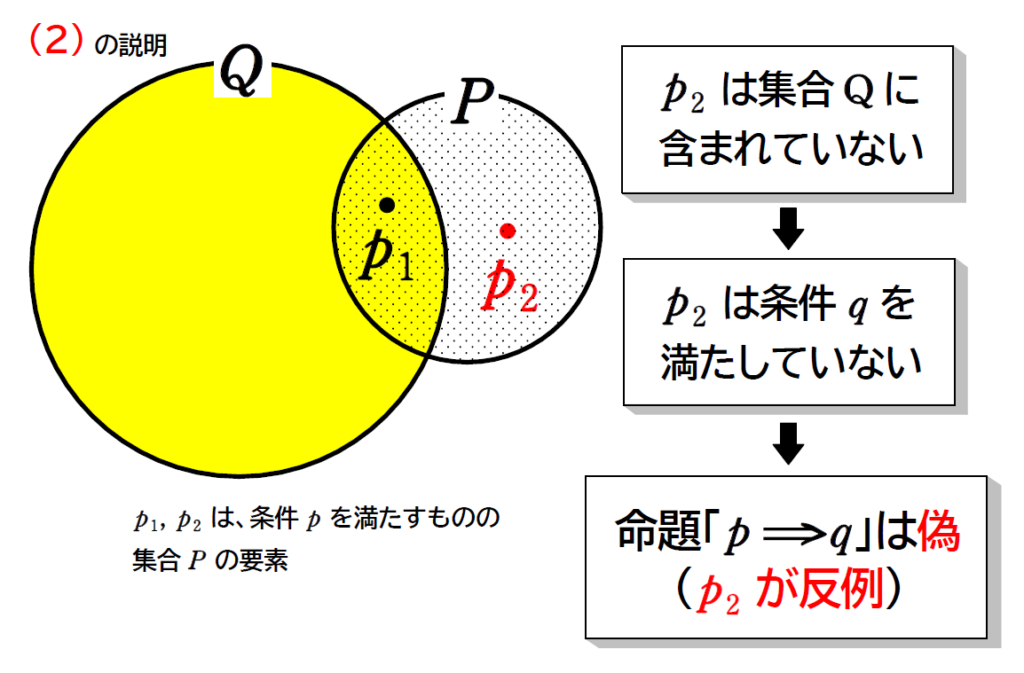
命題「\(\small \,p\ \Rightarrow \ q\,\)」について、条件\(\small \ p,\ q\ \)を満たすものの集合をそれぞれ\(\small \ P,\ Q\ \)とする。
\(\small (1)\) \(\small \color{blue}{P\subset Q}\ \)のとき、命題「\(\small \,p\ \Rightarrow \ q\,\)」は、真。
\(\small(2)\) \(\small \color{red}{P\not\subset Q}\ \)のとき、命題「\(\small \,p\ \Rightarrow \ q\,\)」は、偽。
次の命題の真偽を答えよ。また、偽の場合は反例も答えよ。
\(\small(1)\) \(\small -1≦x≦2\) ならば \(\small x<3\) である。
\(\small(2)\) \(\small -1≦x≦2\) ならば \(\small |x|<2\) である。
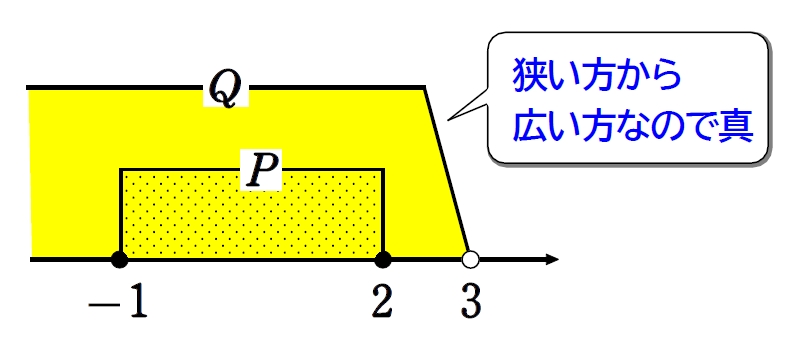
\(\small(1)\) \(\small P=\{x|-1≦x≦2\}\)
\(\small Q=\{x|\,x<3\}\)
とすると、\(\small P\subset Q\) であるから、真
\(\small(2)\) \(\small |x|<2\) の絶対値を外すと、
\(\small -2<x<2\) となる。
\(\small P=\{x|-1≦x≦2\}\)
\(\small Q=\{x|-2<x<2\}\)
とすると、\(\small P\not\subset Q\) であるから、偽
反例は、\(\small x=2\)
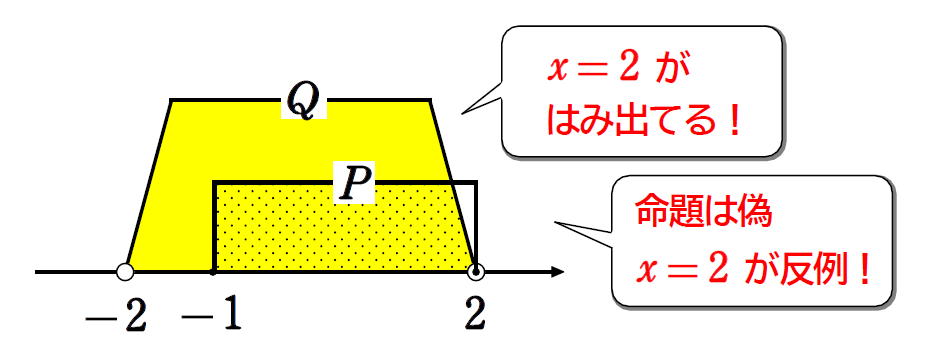
\(\small (2)\) が難しかったですかね?自分がもっている条件、つまり、\(\small -1≦x≦2\) が \(\small x=2\) を含んでいるのに対し、相手からの質問である \(\small |x|<2\) は \(\small x=2\) を含んでいないため、\(\small x=2\) が反例となり偽となりました。
ちなみに絶対値の詳しい説明は、下の記事を見てください。
条件の否定ってナニ?
『集合』の内容の中で、補集合(○○じゃない集合)というものがありました。このときに使ったのが否定です。
実数全体の集合を全体集合とする。
集合 \(\small A=\{\,x\,|\,x<3\,\}\) の補集合は、\(\small \overline{A}=\{\,x\,|\,x≧3\,\}\) である。
詳しくはこちらの記事をみてください。
では、次の例題の問題もみてみましょう。
次の条件の否定を答えよ。
\(\small(1)\) \(\small x>0\) かつ \(\small y>0\)
\(\small(2)\) \(\small x=-1\) または \(\small x=1\)
\(\small (3) \) ある \(\small x\) で \(\small f(x)>0\)
\(\small (4) \) すべての自然数 \(\small n\) で \(\small n^2+n\) は奇数
今回の問題でのポイントは、「かつ」「または」「ある」「すべて」が否定のときにどうなるかです。
「かつ」「または」の否定は『集合』の単元のド・モルガンの法則で習いましたね。
\(\small (1) \overline{A\cap B}=\overline{A}\cup\overline{B}\)
\(\small (2) \overline{A\cup B}=\overline{A}\cap\overline{B}\)
つまり、
条件「\(\small p\) かつ \(\small q\)」の否定は、「(\(\small \,p\) じゃない)または(\(\small \,q\) じゃない)」
条件「\(\small p\) または \(\small q\)」の否定は、「(\(\small \,p\) じゃない)かつ(\(\small \,q\) じゃない)」
となります。
「ある」「すべて」の否定は、次の命題を例に考えてみましょう。
捕まえたポケモンはすべてピカチュウ!!

ピカチュウ?
いやいや、一匹だけ変なのいません?

ミミッキュ
自分の姿をピカチュウに似せているのは、20年ほど前にピカチュウのグッズが流行った際、実は寂しがりやのミミッキュが、その姿なら人間と仲良くできると考えたためなのだ。(公式HPより)
「すべてピカチュウ」というわけではなかったですね…
ということで、正しい文章にするために、この「すべてピカチュウ」を否定してみましょう。1匹ピカチュウではないポケモン、ミミッキュがいたので、「あるポケモンがピカチュウではない!」ということとなります。
まとめると、
となります!!
お待たせしました。解説を見ていきましょう。問題忘れてますかね?下に出しておきますね。
\(\small(1)\) \(\small x>0\) かつ \(\small y>0\)
\(\small(2)\) \(\small x=-1\) または \(\small x=1\)
\(\small (3) \) ある \(\small x\) で \(\small f(x)>0\)
\(\small (4) \) すべての自然数 \(\small n\) で \(\small n^2+n\) は奇数
\(\small(1)\) 「\(\small x>0\) かつ \(\small y>0\)」の否定は、
\(\small x≦0\) または \(\small y≦0\)
\(\small(2)\) 「\(\small x=-1\) または \(\small x=1\)」の否定は、
\(\small x\not=-1\) かつ \(\small x\not=1\)
\(\small (3) \) 「ある \(\small x\) で \(\small f(x)>0\)」の否定は、
すべての \(\small x\) で \(\small f(x)≦0\)
\(\small (4) \) 「すべての自然数 \(\small n\) で \(\small n^2+n\) は奇数」の否定は、
ある自然数 \(\small n\) で \(\small n^2+n\) は偶数
必要条件・十分条件

さて!先ほどの画像で、全部ピカチュウに見えていた人もいたのではないでしょうか?
(いないでしょ!!)
本当にミミッキュが見つかっていましたか!?
(見つかってるでしょうよ…)
では、みんなで一緒にミミッキュを探してみましょう!!
ミミッキュであるためには、耳が黒いことが必要な条件です!
え? ピカユウも耳が黒い? ・・・たしかに!?
ミミッキュであるためには、ほっぺが赤いことが必要な条件です!!
ピカチュウもほっぺは赤いですね・・・
では、これでどうですか!!!
ミミッキュであるためには、「ばけのかわ」の特性をもっている!!!!!
たしかに、「ばけのかわ」の特性をもっているのはミミッキュだけなので、十分すぎる条件ですね。
数学を学ぶ上でも、必要な条件・十分な条件を確認していくことは、非常に重要です。
何かが成り立つために、必要な条件を「必要条件」、十分な条件を「十分条件」といいます。具体例を見ていきましょう。
四角形\(\small \,\rm ABCD\,\)において、 \(\small \,\rm AD/\!/BC\,\) は、四角形\(\small \,\rm ABCD\,\)が平行四辺形であるための何条件か答えよ。
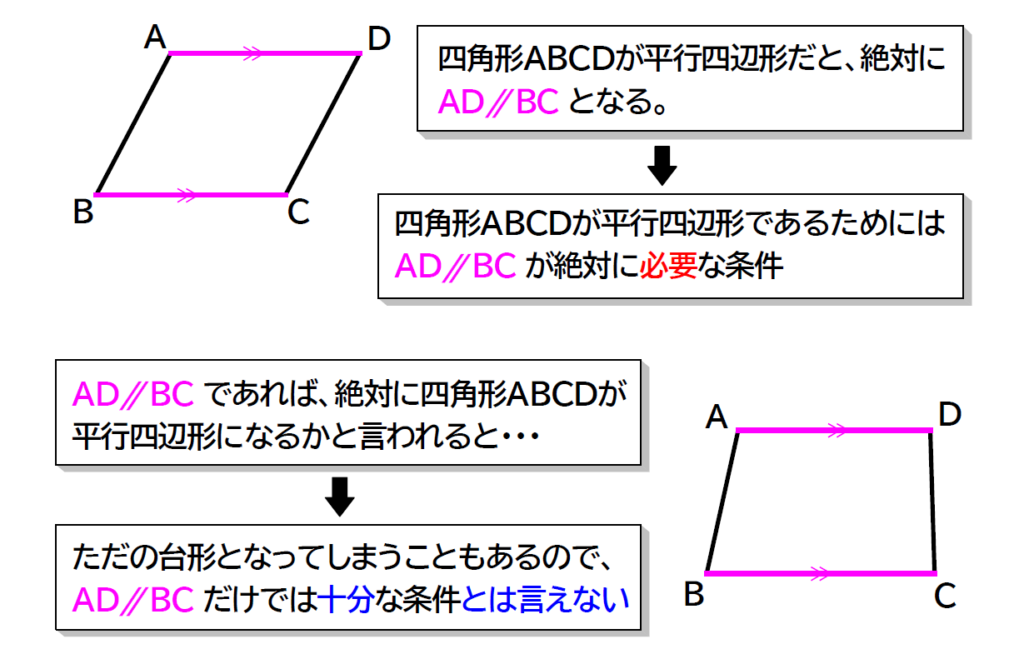
四角形\(\small \,\rm ABCD\,\)が平行四辺形となるためには、向かい合う辺が平行でないといけないので、\(\small \,\rm AD/\!/BC\,\) は必要な条件です。
続いて、\(\small \,\rm AD/\!/BC\,\) であれば、平行四辺形となるための条件として十分かというと、ただの台形となる場合もあるので、十分な条件とは言えません。
つまり、四角形\(\small \,\rm ABCD\,\)において、 \(\small \,\rm AD/\!/BC\,\) は、四角形\(\small \,\rm ABCD\,\)が平行四辺形であるための必要条件であるが十分条件ではない。
実際の問題では、必要な条件なのか、十分な条件なのか判断しづらい場合が多いです。なので、先ほどの例をもとに、公式化しておきましょう!
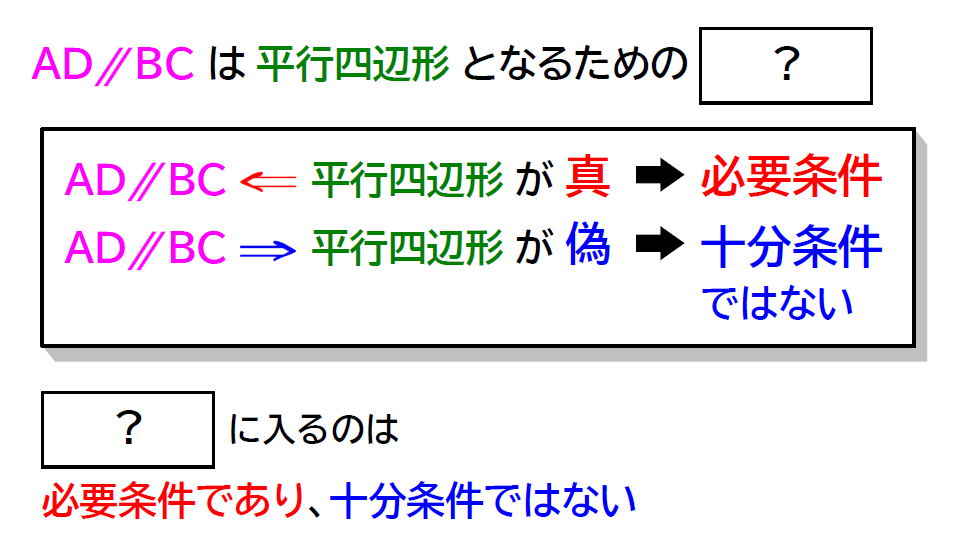
先ほどの例ではどちらの矢印が成立しているかで、何条件となるかが決まりました。
ということで、次のように公式化します。
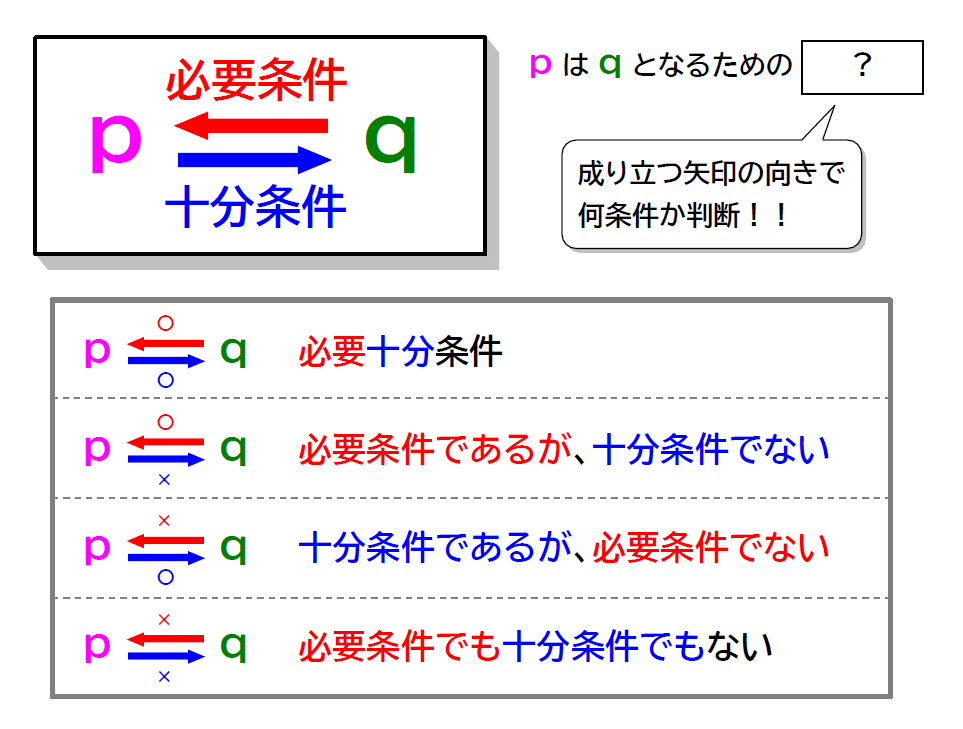
ちなみに、\(\small p \Rightarrow q\) と \(\small q \Rightarrow p\) が成り立つとき、\(\small p \Leftrightarrow q\) と表し、2つの条件は「同値」といいます。
\(\small a,\ b,\ c\) は実数である。条件 \(\small p,\ q\) について、\(\small p\,\)は\(\small \, q\,\)であるための何条件か答えよ。
\(\small(1)\) \(\small p\,:\,a=1,\ b=2 q\,:\,a+b=3\)
\(\small(2)\) \(\small p\,:\,ac=bc q\,:\,a=b\)
\(\small(3)\) \(\small p\,:\,|x|=2 q\,:\,x=\pm2\)
\(\small(4)\) \(\small p\,:\,|x|<1 q\,:\,x^2=4 \)
\(\small(1)\) 「 \(\small a=1,\ b=2 \ \Rightarrow \ a+b=3\) 」は真
「 \(\small a+b=3 \ \Rightarrow \ a=1,\ b=2\) 」は、\(\small a=3,\ b=0 \) が反例となるので偽
よって、十分条件であるが、必要条件ではない。
\(\small(2)\) 「 \(\small ac=bc \ \Rightarrow \ a=b\) 」は、\(\small a=2,\ b=1,\ c=0 \) が反例となるので偽
「 \(\small a=b \ \Rightarrow \ ac=bc\) 」は真
よって、必要条件であるが、十分条件ではない。
\(\small(3)\) \(\small |x|=2\) を解くと、\(\small x=\pm2\) となるので、
「 \(\small |x|=2 \ \Rightarrow \ x=\pm2\) 」は真
「 \(\small x=\pm2 \ \Rightarrow \ |x|=2\) 」も真なので
必要十分条件。
\(\small(4)\) \(\small |x|<1\) を解くと、\(\small -1<x<1\)
\(\small x^2=4 \) を解くと、\(\small x=\pm2\)
「\(\small |x|<1 \ \Rightarrow \ x^2=4\)」は偽(反例:\(\small x=0\))
「\(\small x^2=4 \ \Rightarrow \ |x|<1\)」は偽(反例:\(\small x=2 \))
よって、必要条件でも、十分条件でもない。
必要条件・十分条件を間違えて答えてしまうのは、ほとんどの場合、真偽の判断を間違えることが原因です。ここで、真偽の判断を間違えやすい命題をまとめておきます。
命題『\(\small \,\color{blue}{p} \ \Rightarrow \ \color{magenta}{q}\,\)』の真偽を判断するとき、\(\small p\,\)は自分がもっている条件、\(\small q\,\)は相手からの質問という意識をもって見ていますか?
さて、\(\small a+b>0,\ ab>0\,\)ならば、\(\small a>0,\ b>0\)」が真であることを示していきたいと思います。自分がもっている条件は \(\small a+b>0,\ ab>0\) です。変な言い回しですが、自分がもっている条件は必ず使い切ってください。
- 条件1\( \color{blue}{ab>0}\) を満たす \(\small a,\ b\) を考える
この段階では、\(\small \color{blue}{a>0,\ b>0}\) または \(\small \color{blue}{a<0,\ b<0}\) のどちらの可能性もある。(言い換えると、まだ絶対に \(\small \color{magenta}{a>0,\ b>0}\) とは限らない)
- 条件2\( \color{blue}{a+b>0}\) も満たさないといけない
条件1から \(\small \color{blue}{a>0,\ b>0}\) または \(\small \color{blue}{a<0,\ b<0}\) となっているが、\(\small \color{blue}{a+b>0}\) も満たさないといけません。\(\small \color{blue}{a<0,\ b<0}\) は満たせないので、\(\small \color{blue}{a>0,\ b>0}\) となります。
- 結論相手からの質問 \( \color{magenta}{a>0,\ b>0}\) に対して
自分がもっていた条件1と条件2から、絶対に \(\small \color{magenta}{a>0,\ b>0}\) が成り立ってしまうので真
逆・裏・対偶
命題の逆・裏・対偶ってナニ?
まっくろくろすけ出ておいで、でないと目玉をほじくるぞ~
『となりのトトロ』メイとサツキ


となりのトトロの有名なシーンの一つです。黒いふわふわのものが「まっくろくろすけ」です。あらためて聞くと残忍な一言ですね。
このセリフを命題としてみてみましょう。
まっくろくろすけは出てこないならば、目玉をほじくられる
まっくろくろすけとしては、たまったものではありません。ところで、まっくろくろすけは、出てくることが正解なのでしょうか?問題は、次の命題が真か偽かによります。
まっくろくろすけは出てくれば、目玉をほじくられずに済む
命題②が真か偽かは微妙なところですよね、笑
ところで、数学の世界において、命題①と命題②の議論は重要となってきます。命題①と命題②の関係は数学の用語で「裏」といいます。もう1つ命題をみてみます。
まっくろくろすけの目玉がほじくられるならば、まっくろくろすけは出てきていない
これも偽じゃないでしょうか?そして、命題①と命題③の関係を「逆」といいます。最後にもう1つ命題を見てください。
まっくろくろすけは目玉がほじくられないならば、まっくろくろすけは出てきている
命題①が真なら命題④も真でしょうし、命題①が偽なら命題④も偽でしょうね。命題①と命題④の関係を「対偶」といいます。
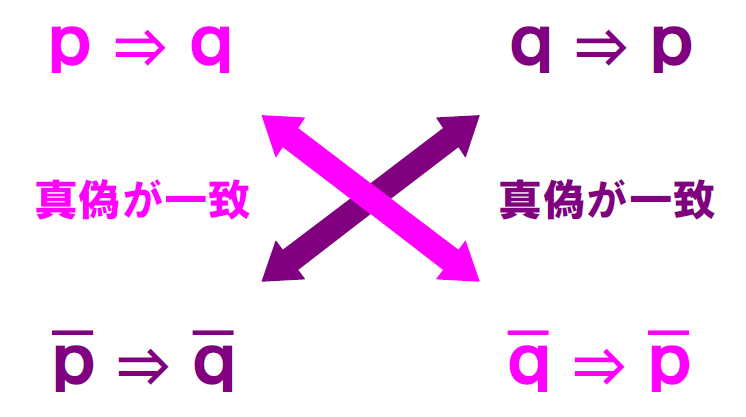
まとめると、
となります。ちなみ「\(\small q \Rightarrow p\)」と「\(\small \bar{p} \Rightarrow \bar{q}\)」は対偶の関係となります。
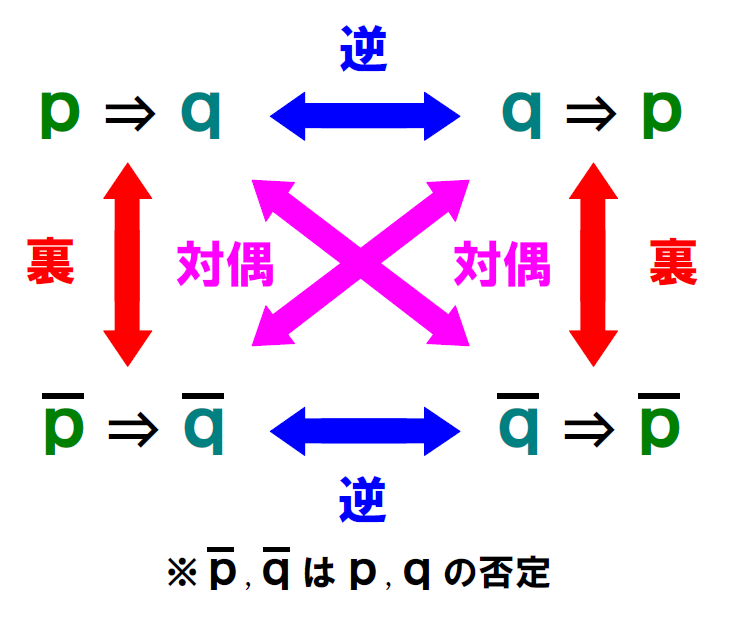
さらに、以下のような特徴もあるので覚えておきましょう。
対偶の関係となる命題の真偽は一致する。
つまり、
\(\small p \Rightarrow q\) と \(\small \bar{q} \Rightarrow \bar{p}\) の真偽、
\(\small q \Rightarrow p\) と \(\small \bar{p} \Rightarrow \bar{q}\) の真偽
は一致する。
次の命題の逆、裏、対偶を述べ、その真偽を答えよ。また、偽であるときは反例を答えよ。
命題『\(\small x=1\) ならば \(\small x^2=1\) である』
逆の関係となる命題は
『\(\small x^2=1\) ならば \(\small x=1\) である』
この命題は、偽(反例:\(\small x=-1\))
裏の関係となる命題は
『\(\small x \not=1\) ならば \(\small x^2\not=1\) である』
この命題は、偽(反例:\(\small x=-1\))
対偶の関係となる命題は
『\(\small x^2 \not=1\) ならば \(\small x\not=1\) である』
この命題は、真
今回の問題では、裏と対偶の真偽が分かりづらかったですよね。
『\(\small x \not=1\) ならば \(\small x^2\not=1\) である』の真偽は、自分のもっている条件が \(\small x\not=1\) で、相手からの質問が \(\small x^2\not=1\) です。

僕のもっている条件は \(\small x\not=1\) だから、1以外の数字は全部考えないと!
\(\scriptsize -2,\ -1,\ \ 0,\ \ 2,\ \ \sqrt{5},\ \ \cdots \)

それって、絶対に \(\small x^2\not=1\) ですか?

ごめんなさい、\(\small x=-1\) だと \(\small x^2=1\) になっちゃいます・・・
ということで、偽となり、反例が \(\small x=-1\) となります。このように考えると、真偽を判断することは不可能ではないですが、大変ですよね。そこで、「対偶の関係となる命題は真偽が一致」することを利用しましょう。
元の命題の 裏 と 逆 は 対偶の関係 ですね。つまり、裏と逆の真偽が一致します。
逆の関係となる『\(\small x^2=1\) ならば \(\small x=1\) である』が偽なのは分かりますね。なので、裏も偽となるということが言えます。また、その際の反例も一致することも確認しておきましょう。
対偶である『\(\small x^2 \not=1\) ならば \(\small x\not=1\) である』の真偽も、元の命題『\(\small x=1\) ならば \(\small x^2=1\) である』の真偽と一致することを利用すると、簡単に真だと分かります。
対偶の使い道ってナニ?
逆・裏・対偶って何のために勉強してるんだろうって思いますよね。それぞれ、色々な利用の仕方がありますが、今回紹介するのは、対偶を証明に利用する方法です。
先ほど、「対偶の関係となる命題は真偽が一致」することを紹介しました。これを利用してみましょう。
整数 \(\small n \) について、\(\small n^2 \) が \(\small 3\) の倍数ならば、\(\small n \)は \(\small 3\) の倍数であることを示せ。
命題『整数 \(\small n \) について、\(\small n^2 \) が \(\small 3\) の倍数ならば、\(\small n \) は \(\small 3\) の倍数である』の対偶は、
『整数 \(\small n \) について、\(\small n \) が \(\small 3\) の倍数でないならば、\(\small n^2 \) は \(\small 3\) の倍数でない』であり、
この命題が真であることを示す。
(\(\small n \) は \(\small 3\) の倍数でないので)
\(\small k\) を整数とすると、
\(\small (ⅰ)\) \(\small n=3k+1\) のとき ( 3の倍数+1のとき )
\(\small\begin{align} n^2&=(3k+1)^2\\&=9k^2+6k+1\\&=\color{blue}{3(3k^2+2k)+1}\end{align}\)
よって、\(\small n^2\) は \(\small 3\) の倍数ではない。
\(\small (ⅱ)\) \(\small n=3k+2\) のとき ( 3の倍数+2のとき )
\(\small\begin{align} n^2&=(3k+2)^2\\&=9k^2+12k+4\\&=\color{blue}{3(3k^2+4k+1)+1}\end{align}\)
よって、\(\small n^2\) は \(\small 3\) の倍数ではない。
\(\small (ⅰ),\,(ⅱ)\ \)より、『整数 \(\small n \) について、\(\small n \) が \(\small 3\) の倍数でないならば、\(\small n^2 \) は \(\small 3\) の倍数でない』は真
よって、『整数 \(\small n \) について、\(\small n^2 \) が \(\small 3\) の倍数ならば、\(\small n \) は \(\small 3\) の倍数である』も真である。
さて、この対偶を利用して証明する方法ですが、使い方も大切ですが、いつ使うかが重要です。
「問題文で言われていることを、そのまま証明できなさそうなときに使う」という方針で良いと思います。
『どのようなときに、そのまま証明できないか』というのをもう少し掘り下げて説明するのであれば、
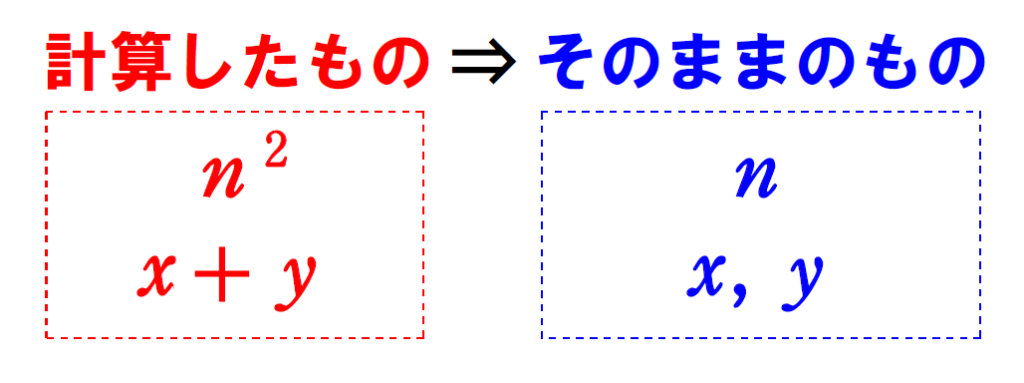
のような流れの証明のときは、そのまま証明することは難しく、対偶を利用することが多いと思います。
定期テストに限って言えば、教科書や学校のプリントなどに出てきたものに絞って練習しておくのが良いと思います。ちなみに、定期テストの勉強に関しては、下の記事も参考にしてください。
背理法ってナニ?

『となりのトトロ』には有名な都市伝説があるのをご存じですか?
「実は物語後半でサツキとメイはすでに死んでいる・・・」というもの。いくつかある理由の中でも最も有名なものが「物語後半からサツキとメイの影が無い」です。確かに作品で確認してみると、影はありません。
ただ、この都市伝説は、公式HPで正式に否定されています。
そもそも、ふつうに作品を見ていれば、「サツキとメイが死んでいるわけがない」ことがすぐに分かります。
「サツキとメイが死んでいた」と仮定します。死んでいるサツキは、トトロに助けを求め、ネコバスを呼んでもらいます。


その後、森の中をネコバスで突っ切り、メイを探します。その際、他の人たちには、ネコバスはもちろん、乗っているサツキも一切見えていません。


確かに、ここまではサツキとメイが死んでいても、おかしくない流れです。
では、次のシーンはいかがでしょうか?

メイが死んでいるのであれば、メイがおばあちゃんと抱き合う事ができません。また、この後、カンタとサツキが話しているシーンがありますが、サツキが死んでいるのであれば、カンタは誰と話しているのでしょうか?
ということで、「サツキとメイが死んでいた」と仮定したとき、さまざまな矛盾が生じます。
よって、「サツキとメイが死んでいるわけがない」と考えるべきです。
さて、この流れで証明していく方法を『背理法』といいます。
『背理法』の流れは、
「事実と反することを仮定」→「仮定に基づき話を進め」→「矛盾を生じさせる」
です。実際の問題で見ていきましょう。
\(\small \sqrt{6}\) が無理数であることを用いて、次のことを示せ。
\(\small (1)\) \(\small 3\sqrt{6}+1\) は無理数
\(\small (2)\) \(\small \sqrt{3}+\sqrt{2}\) は無理数
解答を見る前に、例題の証明をする上での暗黙の了解(ルール)を確認します。
矛盾のさせ方もいくつかパターンがあるので紹介します。
\(\small (1)\) \(\small 3\sqrt{6}+1=r\) (\(\small \,r\) は有理数) と仮定すると、
\(\small \displaystyle \sqrt{6}=\frac{r-1}{3}\)
(無理数)\(\small=\)(有理数) となり、矛盾するので、
\(\small 3\sqrt{6}+1\) は無理数である。
\(\small (2)\) \(\small \sqrt{3}+\sqrt{2}=r\) (\(\small \,r\) は有理数) と仮定すると、両辺を2乗して
\(\small \left(\sqrt{3}+\sqrt{2}\right)^2=r^2\)
\(\small 5+2\sqrt{6}=r^2\)
\(\small \displaystyle\sqrt{6}=\frac{r^2-5}{2}\)
(無理数)\(\small=\)(有理数) となり、矛盾するので、
\(\small \sqrt{3}+\sqrt{2}\) は無理数である。
続いては、定期テストではお馴染みの背理法を使った証明です。
\(\small \sqrt{3}\) が無理数であることを示せ。

最後に、いつ背理法を使うのかを確認しておきます。
否定の証明 \(\small \Rightarrow \) 背理法
これは今後の数学でも応用問題などで大活躍する話なので頭に入れておきましょう。
まとめ
必要条件、十分条件、逆・裏・対偶などは、それ自体の意味も重要ですが、命題の真偽を正確に把握することがポイントになります。また、背理法などを使う証明問題は理解するだけでも大変だったりします。一問ずつじっくりと考えながら解いていき、理解を深めていきましょう。








コメント