こんにちは。ねこの数式のnanakoです。
今回は、判別式と2次不等式を中心に仕組みまでしっかりと理解して、応用問題を解けるようにするための準備をしていきましょう。
2次方程式
2次不等式などの話に入る前に、2次方程式を見ていきます。
2次方程式を解く上で、因数分解できないときって、どうすれば良かったか覚えていますか?
解の公式
2次方程式\(\small \, ax^2+bx+c=0\,\)の解は、
\(\small \displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
特に、\(\small b\) が偶数のとき、\(\small b=2b’\) とすると、
\(\small \displaystyle x=\frac{-b’\pm\sqrt{b’^2-ac}}{a}\)

因数分解ができない2次方程式に対して使っていく公式になります。
次の方程式を解け。
\(\small (1)\) \(\small 2x^2+3x-1=0 \)
\(\small (2)\) \(\small 5x^2-4x-3=0 \)
\(\small \begin{align}(1) \displaystyle x&=\frac{-3\pm\sqrt{3^2-4\cdot 2 \cdot (-1)}}{2\cdot 2}\\[5pt] &=\frac{-3\pm\sqrt{17}}{4}\end{align}\)
\(\small \begin{align}(2) \displaystyle x&=\frac{-(-2)\pm\sqrt{(-2)^2-5 \cdot (-3)}}{5}\\[5pt] &=\frac{2\pm\sqrt{19}}{5}\end{align}\)
さて、続いては、解の個数についてみていきます。
判別式
突然ですが、2次方程式 \(\small x^2-6x+9=0\) の解の個数は何個ですか?
実際に解いて解を求めてみましょう。
\(\small x^2-6x+9=0 \) を因数分解すると、\(\small (x-3)^2=0 \)
これを解くと \(\small x=3 \)
さて、解の個数は何個ですか?
1個だと思いましたよね~?
これが数学の世界の面倒くさいところ・・・
さきほどの方程式は、\(\small (x-3)(x-3)=0 \) と表せるので、それぞれのカッコから \(\small x=3 \) が出てきます。
よって、\(\small 3\,\)が\(\small \,2\,\)つ出てくるので、解の個数は2つとなるんです。
続いては、方程式 \(\small x^2=-1 \) の解の個数はどうでしょう?
2乗して \(\small -1\) になる数なんてないって思いますよね。実は、数Ⅱで新しい数『虚数』というものが現れます。
\(\small x^2=-1 \) を解くと、\(\small x=\pm\sqrt{-1}\) となる。
\(\small \sqrt{-1}=i\) (\(\small i \) は虚数単位)とし、これを用いた数を虚数と呼びます。
(今まで習ってきた数字が実数で、実数じゃない数が虚数です)
つまり、\(\small x^2=-1\) の解は \(\small \pm\sqrt{-1}\) の2個存在することとなります。
そうなると、2次方程式は、なんでもかんでも解の個数が2個となってしまいますね。
ということで、2次方程式の解の個数を区別して答えられるように、言葉遣いを整理しましょう。
ようやく、本題の『判別式』に入ります。判別式とは、2次方程式の解の個数について調べるものです。

2次方程式\(\small \, ax^2+bx+c=0\,\)について、\(\small D=b^2-4ac\) を 判別式 という。2次方程式の解は、
① \(\small D>0\) のとき、異なる2つの実数解
② \(\small D=0\) のとき、重解
③ \(\small D<0\) のとき、実数解なし
となる。
2次方程式が\(\small \, ax^2+2b’x+c=0\,\)の形のときは、解の公式は
\(\small \displaystyle x=\frac{-b’\pm\sqrt{b’^2-ac}}{a}\)
でした。このときの判別式は、\(\small D/4=b’^2-ac\) と表されます。
役割は \(\small D\) と全く同じで、
① \(\small D/4>0\) のとき、異なる2つの実数解
② \(\small D/4=0\) のとき、重解
③ \(\small D/4<0\) のとき、実数解なし
となります。
次の2次方程式の異なる実数解の個数を調べよ。
\(\small (1) \) \(\small 2x^2-3x+5=0\)
\(\small (2) \) \(\small 9x^2-6x+1=0\)
\(\small (1) \) 判別式を \(\small D \) とすると、
\(\small D=(-3)^2-4\cdot 2 \cdot 5=-31\color{blue}{<0} \)
よって、0個(実数解なし)
\(\small (2) \) 判別式を \(\small D \) とすると、
\(\small D/4=(-3)^2-9\cdot 1\color{magenta}{=0}\)
よって、1個(重解)
次の問いに答えよ。
\(\small (1)\) 2次方程式 \(\small x^2-3x+k+2=0\) が異なる\(\small \, 2\, \)つの実数解をもつときの定数 \(\small k \) のとり得る値の範囲を求めよ。
\(\small (2)\) 2次方程式 \(\small x^2+2kx+2k+3=0\) が重解をもつときの \(\small k\) の値と、そのときの重解を求めよ。
\(\small (1)\) 判別式を \(\small D \) とすると、
異なる\(\small \, 2\, \)つの実数解をもつので、\(\small \color{red}{D>0}\) となる。
よって、\(\small D=(-3)^2-4\cdot 1\cdot (k+2)\color{red}{>0} \)
これを解くと \(\small \displaystyle k<\frac{1}{4}\)
\(\small (2)\) \(\small x^2+2kx+2k+3=0\ \ \cdots \,\)①
判別式を \(\small D \) とすると、
重解をもつので、\(\small \color{magenta}{D=0}\) となる。
よって、\(\small D/4=k^2-1\cdot(2k+3)\color{magenta}{=0} \)
因数分解すると、\(\small (k+3))(k-1)=0 \)
これを解くと \(\small k=-3,\, 1\)
\(\small (\normalsizeⅰ\small )\) \(\small k=-3\) のとき、① は \(\small x^2-6x+9=0\)
因数分解すると、\(\small (x-3)^2=0\)
これを解くと \(\small x=3 \)
\(\small (\normalsizeⅱ\small )\) \(\small k=1\) のとき、① は \(\small x^2-2x+1=0\)
因数分解すると、\(\small (x-1)^2=0\)
これを解くと \(\small x=1 \)
\(\small (\normalsizeⅰ\small ),(\normalsizeⅱ\small )\) より、\(\begin{cases}\small k=-3 \,\normalsize のとき、重解は \, \small3\\
\small k=1 \, \normalsize のとき、重解は \, \small -1\end{cases}\)
放物線とx軸の共有点
さて、まずは「交点」「接点」「共有点」という用語の違いを確認して…して…シテ…シte…site…していきたくないです。というのも、数学の闇みたいな話で、「交点」という用語が明確に定義されていない(決まっていない)んです。たぶん・・・(-_-;)
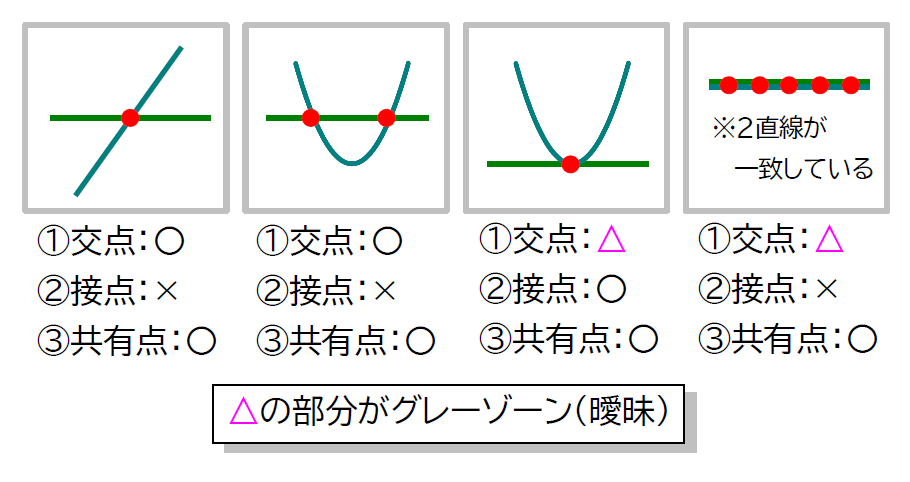
「交わる」という言葉の定義が曖昧なのが原因で、交点という言葉を使うと余計な議論を生むので、共有点という言葉を使おうというのが世論です。共有点とは、2つ以上のグラフが共有する点のことです。
これ以上、深追いするのはやめましょう。
では、放物線と\(\small \, x\,\)軸との共有点の問題を見ていきます。
放物線\(\small \, y=x^2-2x-8 \,\)と\(\small \,x\,\)軸の共有点の座標を求めよ。
\(\small x\,\)軸上の点は、\(\small y\,\)座標は0なので、次のような解答となります。
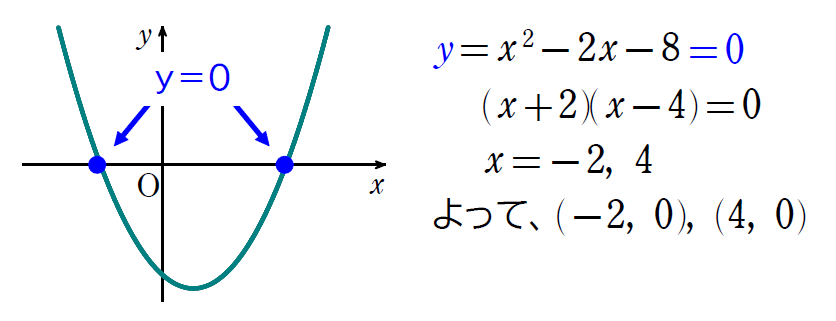
放物線\(\small \, y=x^2-4x-k-1 \,\)が\(\small \,x\,\)軸と異なる \(\small 2\) 点で交わるときの \(\small k\) の値の範囲を求めよ。
条件より、\(\small y\, \)座標が\(\small \,0\, \)となる点が2つあるので、\(\small y=x^2-4x-k-1=0 \) が異なる2つの実数解をもつ。よって、判別式を \(\small D \) とすると、
\(\small D/4=(-2)^2-1\cdot(-k-1)>0 \)
これを解くと \(\small k>-5\)
2次不等式
さて、これまでの問題でも使用してきた1次不等式は、みなさん大丈夫ですね。
2次不等式の解法の仕組み
\(\small x\) が1乗までしか無かったのが1次不等式です。2次不等式は、\(\small x^2\) が含まれる不等式のことをいいます。2次不等式の解法は、1次不等式とは全く異なります。誘導に乗りつつ、2次不等式の解き方を理解していきましょう。
次の問いに答えよ。
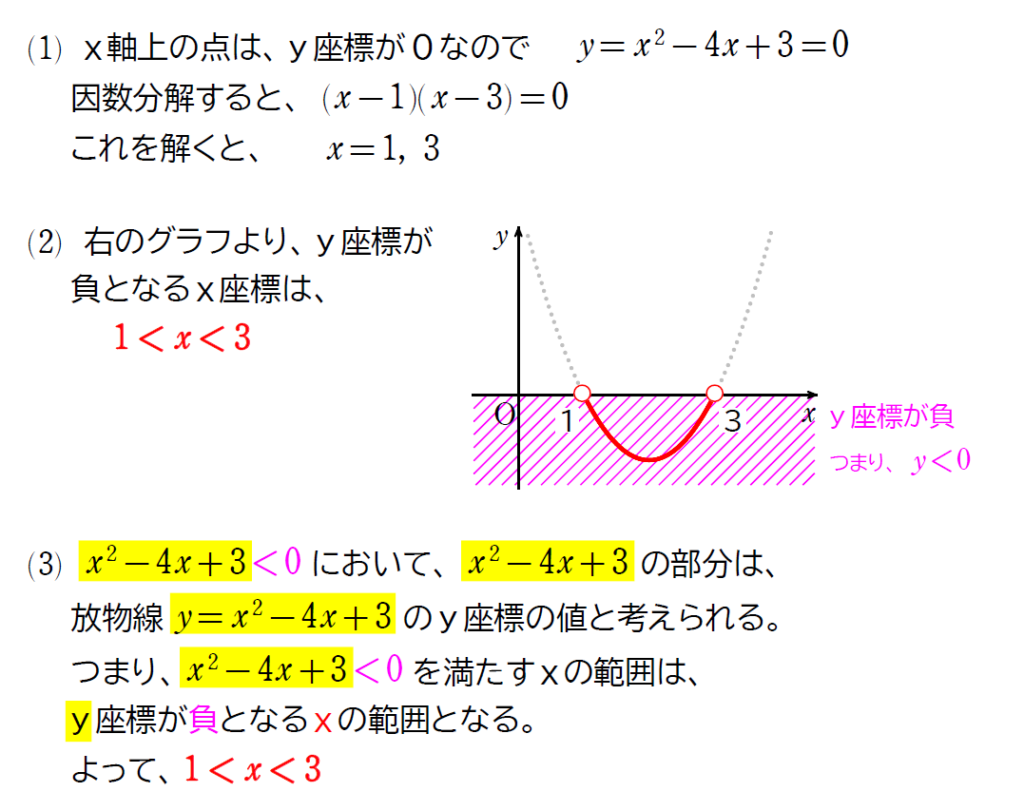
\(\small (1)\) 放物線 \(\small y=x^2-4x+3 \) と\(\small \,x\, \)軸の共有点の\(\small \,x\, \)座標を求めよ。
\(\small (2)\) \(\small y \, \)座標が負となる\(\small \,x\,\)の範囲を求めよ。
\(\small (3) \) 2次不等式\(\small \, x^2-4x+3<0\,\)を解け。
解法の流れはつかめたでしょうか? 実際の解答の書き方などを確認するためにも、あと数問解いてみましょう。
次の2次不等式を解け。
\(\small (1)\) \(\small x^2-5x+6≧0\)
\(\small (2)\) \(\small 2x^2-x-3<0\)
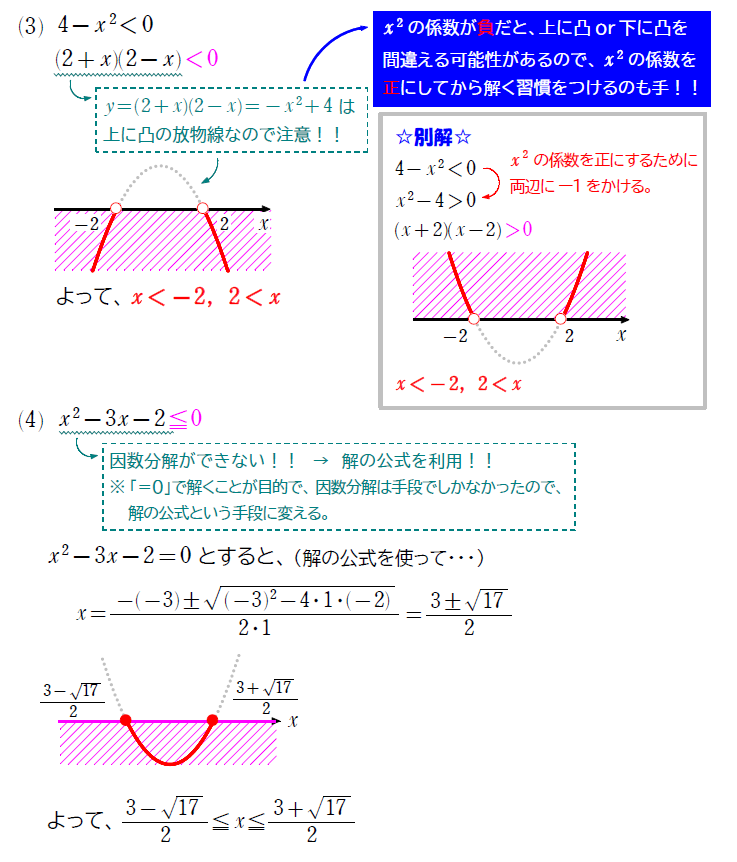
\(\small (3)\) \(\small 4-x^2<0\)
\(\small (4) \) \(\small x^2-3x-1≦0\)

続いては、放物線が\(\small \, x\,\)軸と異なる2点で交わらないケースの問題です。
次の2次不等式を解け。
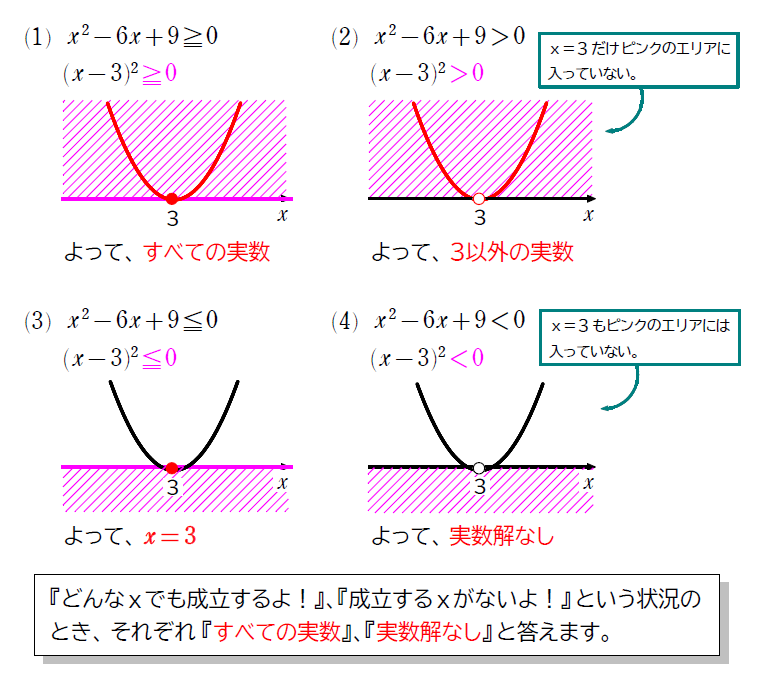
\(\small (1)\) \(\small x^2-6x+9≧0\)
\(\small (2)\) \(\small x^2-6x+9>0\)
\(\small (3)\) \(\small x^2-6x+9≦0\)
\(\small (4) \) \(\small x^2-6x+9<0\)
次の2次不等式を解け。
\(\small (1) \) \(\small x^2-4x+5>0\)
\(\small (2) \) \(\small x^2-4x+5<0\)

2次不等式はこれから数学の問題を解く上で、必需品となるものです。しっかりと練習しておきましょう。
絶対不等式
どんな\(\small \,x\,\)でも成立する不等式を絶対不等式と呼びます。実際の問題を見てみましょう。
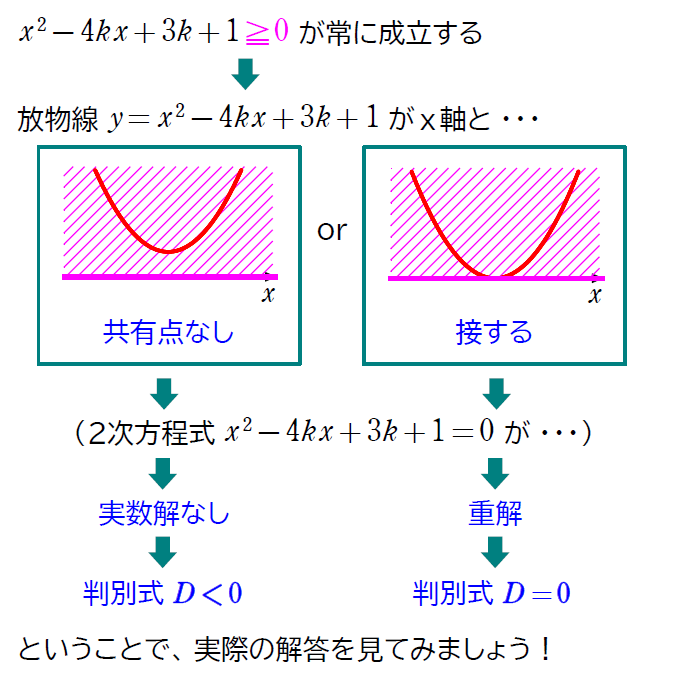
次の不等式が常に成立するような定数\(\small \,k\,\)のとり得る値の範囲を求めよ。
\(\small x^2-4kx+3k+1≧0\)
これまでの判別式や2不等式の話がちゃんと理解できていないと、不等号の向きが逆になってしまう問題です。

まとめ
解の公式、判別式、2次不等式は、これからの数学でずっとお世話になるものです。これ以降の問題では、細かい説明抜きで、さらっと使用することが多いので、このタイミングでしっかりと理解しておきましょう」。






コメント